Cross Multiplication – Techniques & Examples

Before we can discuss the cross-multiplication process, let’s remind ourselves about the parts of a fraction. A fraction normally is a number written in the form a/b where a and b are integers and b is a non-zero.

The number at the top in a fraction is known as the numerator, while the number at the bottom is known as the denominator. The numerator and denominator are separated by a slash line or division bar.

For instance, 4/5, 2/7, 1/3, 1/4, etc., are all examples of fractions. It is also important to note that a rational expression similarly takes a fraction a/b, where a and b are algebraic expressions.

Examples of rational expressions are; (x +5)/3, 2/x- 8, 3x/5 etc.

What is Cross Multiplication?

In mathematics, cross multiplication occurs when a variable in an equation is determined by cross multiplying two fractions or expressions. Cross multiplication can be applied also compare fractions by multiplying the numerator of each fraction by the other’s denominator.

How to Cross Multiply?

The numerator of the first fraction is multiplied with the denominator of the second fraction to perform cross multiplication. Similarly, the denominator of the first fraction is multiplied by the numerator of the second fraction.

The two products are equated, and the value of the variable is determined.

To master how to do cross multiplication, let’s examine the following cross multiplication cases:

How to cross multiply with a variable?

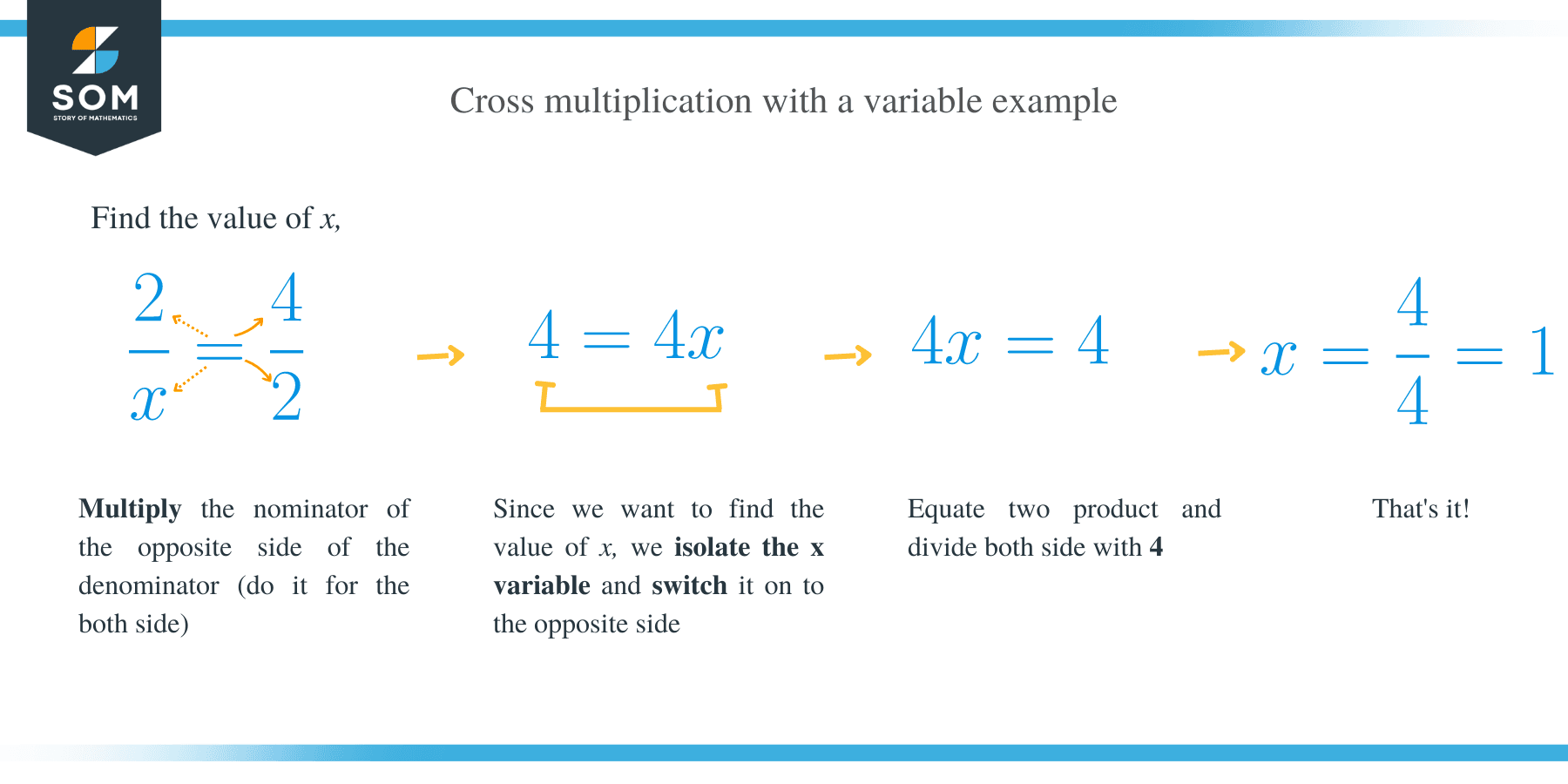
Example 1

Given, 9/x = 3/2

Solution

To find the value of x, we apply the cross-multiplication process where;

• Multiply the numerator of the first fraction by the denominator of the second fraction;

9* 2 =18

• Similarly, multiply the denominator of the first fraction by the numerator of the second fraction;

x * 3 =3x

• Now equate the two products and divide both sides of the equation by 3;

3x = 18

x =6

Example 2

Solve x/5 = 4/2

Solution

Apply the same procedures for cross multiplication;

• x * 2 = 2x
• 5 * 4 = 20

Now equate the two products;

2x = 20

x = 10

Cross Multiplying with two of the Same Variable

Example 3

(x + 3)/2 = (x +1)/1

Solution

In this case, the numerator of the first and second fractions are x +3 and x + 1, respectively.

Now, apply cross-multiplication by multiplying the numerator of the first fraction by the denominator of the second fraction;

• (x + 3) * 1 = x + 3

Multiply dominator of 1^ST fraction by numerator of 2^ND fraction;

• 2 * (x + 1) = 2x + 2

Equate the two products and combine the like terms

• 4x + 12 = 2x + 2.

Isolate the variable x by adding -2x to both sides of the equation;

• 4x -2x +12 = 2x -2x + 2

= 2x + 12 = 2

Now add -12 to both sides,

• 2x + 12 -12 = 2 -12

2x = -10

x = -5

Example 4

Solve 8/ (x – 2) = 4/x

Solution

Cross multiply;

• 8 * x = 8x
• (x- 2) * 4= 4x – 8

Equate the two products and combine the like terms;

8x = 4x -8

Isolate the variable x;

• Add -4x to both sides of the equation;

8x – 4x = 8

4x = 8

x = 2

Example 5

Solve for x 2x/3 + x/2 = 5/6

Solution

In this case, we multiply each term by the LCM. The LCM of 3, 2 and 6 is 6, Therefore, the equation will be;

• (2x/3)6 + (x/2)6 = (5/6)6

= 4x + 3x = 5

Combine the like terms and divide both sides by 7;

7x = 5

x = 5/7

Example 6

Solve for x 4/10 = x/15

Solution

Cross multiply and equate the products;
4 * 15 = 10 * x

Divide both sides of the equation by 10;

x = 60/10

= 6