- Home
- >
- Difference of Squares – Explanation & Examples
JUMP TO TOPIC
Difference of Squares – Explanation & Examples
 A quadratic equation is a second degree polynomial usually in the form of f(x) = ax2 + bx + c where a, b, c, ∈ R, and a ≠ 0. The term ‘a’ is referred to as the leading coefficient, while ‘c’ is the absolute term of f (x). Every quadratic equation has two values of the unknown variable, usually known as the roots of the equation (α, β).
A quadratic equation is a second degree polynomial usually in the form of f(x) = ax2 + bx + c where a, b, c, ∈ R, and a ≠ 0. The term ‘a’ is referred to as the leading coefficient, while ‘c’ is the absolute term of f (x). Every quadratic equation has two values of the unknown variable, usually known as the roots of the equation (α, β).
What is Difference of Squares?
The difference of two squares is a theorem that tells us if a quadratic equation can be written as a product of two binomials, in which one shows the difference of the square roots and the other shows the sum of the square roots.
One thing to note about this theorem is that it does not apply to the SUM of squares.
Difference of Squares Formula
The difference of square formula is an algebraic form of the equation used to express the differences between two square values. A difference of square is expressed in the form:
a2 – b2, where both the first and last term is perfect squares. Factoring the difference of the two squares gives:
a2 – b2 = (a + b) (a – b)
This is true because, (a + b) (a – b) = a2 – ab + ab – b2 = a2 – b2
 How to Factor Difference of Squares?
How to Factor Difference of Squares?
In this section, we will learn how to factorize algebraic expressions using the difference of square formula. To factor a difference of squares, the following steps are undertaken:
- Check if the terms have the greatest common factor (GCF) and factor it out. Remember to include the GCF in your final answer.
- Determine the numbers that will produce the same results and apply the formula: a2– b2 = (a + b) (a – b) or (a – b) (a + b)
- Check whether you can factor the remaining terms any further.
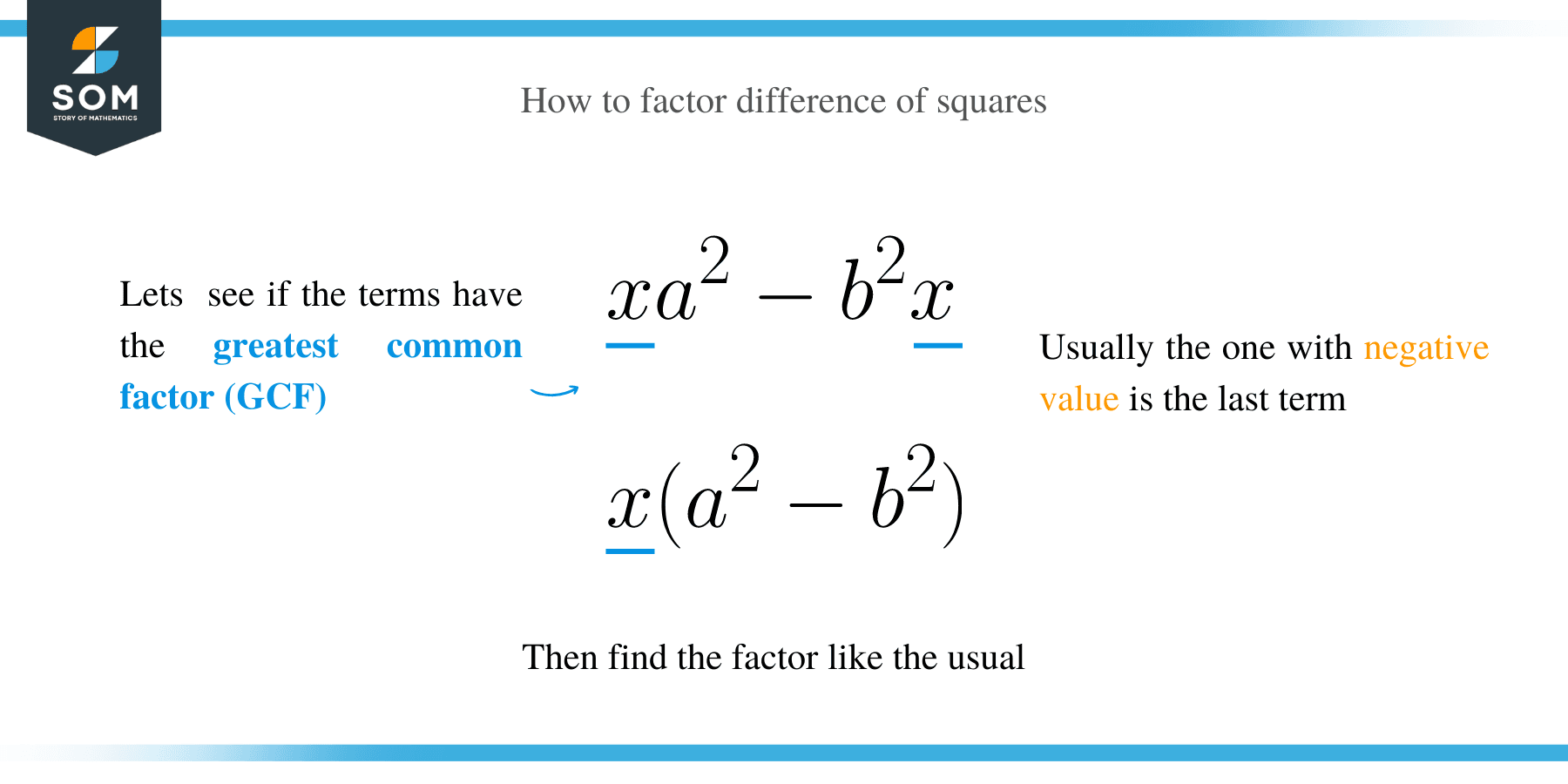 Let’s solve a few examples by applying these steps.
Let’s solve a few examples by applying these steps.
Example 1
Factor 64 – x2
Solution
Since we know the square of 8 is 64, then we can rewrite the expression as;
64 – x2 = (8)2 – x2
Now, apply the formula a2 – b2 = (a + b) (a – b) to factorize expression;
= (8 + x) (8 – x).
Example 2
Factorize
x 2 −16
Solution
Since x2−16 = (x) 2− (4)2, therefore apply the difference square formula a2 – b2 = (a + b) (a – b), where a and b in this case are x and 4 respectively.
Therefore, x2 – 42 = (x + 4) (x – 4)
Example 3
Factor 3a2 – 27b2
Solution
Since 3 is GCF of the terms, we factor it out.
3a2 – 27b2 = 3(a2 – 9b2)
=3[(a)2 – (3b)2]
Now apply a2 – b2 = (a + b) (a – b) to get;
= 3(a + 3b) (a – 3b)
Example 4
Factor x3 – 25x
Solution
Since the GCF = x, factor it out;
x3 – 25x = x (x2 – 25)
= x (x2 – 52)
Apply the formula a2 – b2 = (a + b) (a – b) to get;
= x (x + 5) (x – 5).
Example 5
Factor the expression (x – 2)2 – (x – 3)2
Solution
In this problem a = (x – 2) and b = (x – 3)
We now apply a2 – b2 = (a + b) (a – b)
= [(x – 2) + (x – 3)] [(x – 2) – (x – 3)]
= [x – 2 + x – 3] [x – 2 – x + 3]
Combine the like terms and simplify the expressions;
[x – 2 + x – 3] [x – 2 – x + 3] = > [2x – 5] [1]
= [2x – 5]
Example 6
Factor the expression 25(x + y)2 – 36(x – 2y)2.
Solution
Rewrite the expression in the form a2 – b2.
25(x + y)2 – 36(x – 2y)2 => {5(x + y)}2 – {6(x – 2y)}2
Apply the formula a2 – b2 = (a + b) (a – b) to get,
= [5(x + y) + 6(x – 2y)] [5(x + y) – 6(x – 2y)]
= [5x + 5y + 6x – 12y] [5x + 5y – 6x + 12y]
Collect like terms and simplify;
= (11x – 7y) (17y – x).
Example 7
Factor 2x2– 32.
Solution
Factor out the GCF;
2x2– 32 => 2(x2– 16)
= 2(x2 – 42)
Applying the difference squares formula, we get;
= 2(x + 4) (x – 4)
Example 8
Factor 9x6 – y8
Solution
First, rewrite 9x6 – y8 in the form a2 – b2.
9x6 – y8 => (3x3)2 – (y4)2
Apply a2 – b2 = (a + b) (a – b) to get;
= (3x3 – y4) (3x3 + y4)
Example 9
Factor the expression 81a2 – (b – c)2
Solution
Rewrite 81a2 – (b – c)2 as a2 – b2
= (9a)2 – (b – c)2
By applying the formula of a2 – b2 = (a + b) (a – b) we get,
= [9a + (b – c)] [9a – (b – c)]
= [9a + b – c] [9a – b + c ]
Example 10
Factor 4x2– 25
Solution
= (2x)2– (5)2
= (2x + 5) (2x – 5

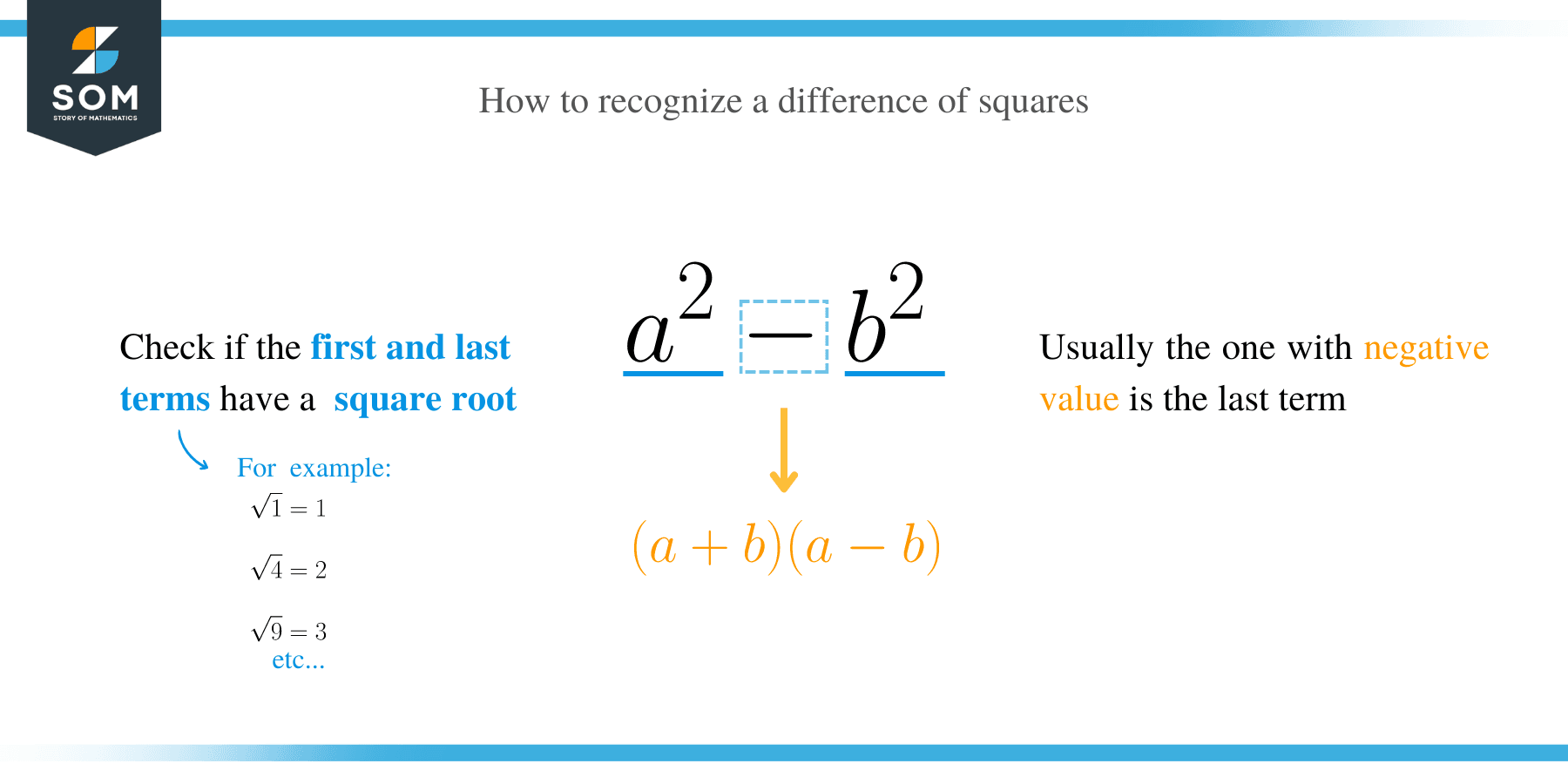 How to Factor Difference of Squares?
How to Factor Difference of Squares?