- Home
- >
- Dividing Rational Expressions – Techniques & Examples
Dividing Rational Expressions – Techniques & Examples
 Rational expressions in mathematics can be defined as fractions in which either or both the numerator and the denominator are polynomials. Just like dividing fractions, rational expressions are divided by applying the same rules and procedures.
Rational expressions in mathematics can be defined as fractions in which either or both the numerator and the denominator are polynomials. Just like dividing fractions, rational expressions are divided by applying the same rules and procedures.
To divide two fractions, we multiply the first fraction by the inverse of the second fraction. This is done by changing from the division sign (÷) to the multiplication sign (×).
The general formula for dividing fractions and rational expressions is;
- a/b ÷ c/d = a/b × d/c = ad/bc
For example;
- 5/7 ÷ 9/49 = 5/7 × 49/9
= (5 × 49)/ (7 × 9) = 245/63
= 35/9
- 9/16 ÷ 5/8
= 9/16 × 8/5
= (9 × 8)/ (16 × 5)
= 72/80
= 9/10
How to Divide Rational Expressions?
Dividing rational expressions follow the same rule of dividing two numerical fractions.
The steps involved in dividing two rational expressions are:
- Factor both the numerators and denominators of each fraction. You must know how to factor quadratic and cubic equations.
- Change from division to multiplication sign and flip the rational expressions after the operation sign.
- Simplify the fractions by canceling common terms in the numerators and denominators. Take care that you cancel the factors and not the terms.
- Finally, rewrite the remaining expressions.
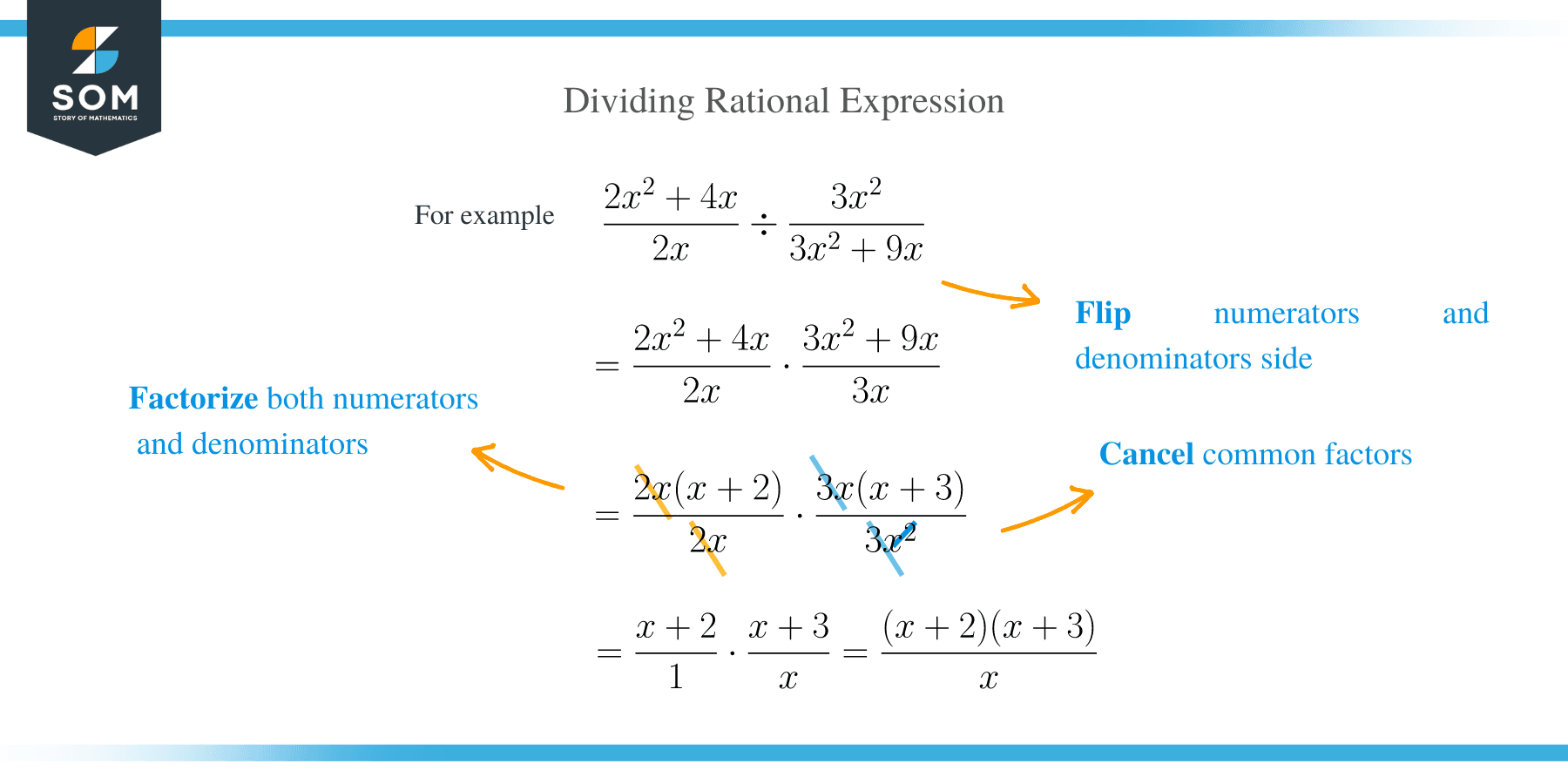 Below are the few examples which will better explain the dividing rational expression technique.
Below are the few examples which will better explain the dividing rational expression technique.
Example 1
[(x2 + 3x – 28)/ (x2 + 4x + 4)] ÷ [(x2 – 49)/ (x2 – 5x- 14)]
Solution
= (x2 + 3x – 28)/ (x2 + 4x + 4)] ÷ [(x2 – 49)/ (x2 – 5x – 14)
Factor both the numerators and denominators of each fraction.
⟹ x2 + 3x – 28 = (x – 4) (x + 7)
⟹ x2 + 4x + 4 = (x + 2) (x + 2)
⟹ x2 – 49 = x2 – 72 = (x – 7) (x + 7)
⟹ x2 – 5x – 14 = (x – 7) (x + 2)
= [(x – 4) (x + 7)/ (x + 2) (x + 2)] ÷ [(x -7) (x + 7)/ (x – 7) (x + 2)]
Now, multiply the first fraction by the reciprocal of the second fraction.
= [(x – 4) (x + 7)/ (x + 2) (x + 2)] * [(x – 7) (x + 2)/ (x – 7) (x + 7)]
On cancelling common terms and rewrite the remaining factors to get;
= (x – 4)/ (x + 2)
Example 2
Divide [(2t2 + 5t + 3)/ (2t2 +7t +6)] ÷ [(t2 + 6t + 5)/ (-5t2 – 35t – 50)]
Solution
Factor the numerators and denominators of each fraction.
⟹ 2t2 + 5t + 3 = (t + 1) (2t + 3)
⟹ 2t2 + 7t + 6 = (2t + 3) (t + 2)
⟹ t2 + 6t + 5 = (t + 1) (t + 5)
⟹ -5t2 – 35t -50 = -5(t2 + 7t + 10)
= -5(t + 2) (t + 5)
= [(t + 1) (2t + 3)/ (2t + 3) (t + 2)] ÷ [(t + 1) (t + 5)/-5(t + 2) (t + 5)]
Multiply by the reciprocal of the second rational expression.
= [(t + 1) (2t + 3)/ (2t + 3) (t + 2)] * [-5(t + 2) (t + 5)/ (t + 1) (t + 5)]
Cancel common terms.
= -5
Example 3
[(x + 2)/4y] ÷ [(x2 – x – 6)/12y2]
Solution
Factor the numerators of the second fraction
⟹ (x2 – x – 6) = (x – 3) (x + 2)
= [(x + 2)/4y] ÷ [(x – 3) (x + 2)/12y2]
Multiply by the reciprocal
= [(x + 2)/4y] * [12y2/ (x – 3) (x + 2)]
On cancelling common terms, we get the answer as;
= 3y/4(x – 3)
Example 4
Simplify [(12y2 – 22y + 8)/3y] ÷ [(3y2 + 2y – 8)/ (2y2 + 4y)]
Solution
Factor the expressions.
⟹ 12y2 – 22y + 8 = 2(6y2 – 11y + 4)
= 2(3y – 4) (2y – 1)
⟹ (3y2 + 2y – 8) = (y + 2) (3y – 4)
= 2y2 + 4y = 2y (y + 2)
= [(12y2 – 22y + 8)/3y] ÷ [(3y2 + 2y – 8)/ (2y2 + 4y)]
= [2(3y – 4) (y – 1)/3y] ÷ [y + 2) (3y – 4)/2y (y + 2)]
= [2(3y – 4) (2y – 1)/3y] * [y (y + 2)/ (y + 2) (3y – 4)]
= 4(2y – 1)/3
Example 5
Simplify (14x4/y) ÷ (7x/3y4).
Solution
= (14x4/y) ÷ (7x/3y4)
= (14x4/ y) * (3y4/7x)
= (14x4 * 3y4) / 7xy
= 6x3y3
