Factoring Quadratic Equations – Methods & Examples

Do you have any idea about the factorization of polynomials? Since you now have some basic information about polynomials, we will learn how to solve quadratic polynomials by factorization.

First of all, let’s take a quick review of the quadratic equation. A quadratic equation is a polynomial of a second degree, usually in the form of f(x) = ax² + bx + c where a, b, c, ∈ R, and a ≠ 0. The term ‘a’ is referred to as the leading coefficient, while ‘c’ is the absolute term of f (x).

Every quadratic equation has two values of the unknown variable, usually known as the roots of the equation (α, β). We can obtain the roots of a quadratic equation by factoring the equation.

For this reason, factorization is a fundamental step towards solving any equation in mathematics. Let’s find out.

How to Factor a Quadratic Equation?

Factoring a quadratic equation can be defined as the process of breaking the equation into the product of its factors. In other words, we can also say that factorization is the reverse of multiplying out.

To solve the quadratic equation ax ² + bx + c = 0 by factorization, the following steps are used:

• Expand the expression and clear all fractions if necessary.
• Move all terms to the left-hand side of the equal to sign.
• Factorize the equation by breaking down the middle term.
• Equate each factor to zero and solve the linear equations

Example 1

Solve: 2(x ² + 1) = 5x

Solution

Expand the equation and move all the terms to the left of the equal sign.

⟹ 2x ² – 5x + 2 = 0

⟹ 2x ² – 4x – x + 2 = 0

⟹ 2x (x – 2) – 1(x – 2) = 0

⟹ (x – 2) (2x – 1) = 0

Equate each factor equal to zero and solve

⟹ x – 2 = 0 or 2x – 1 = 0

⟹ x = 2 or x = 1212

Therefore, the solutions are x = 2, 1/2.

Example 2

Solve 3x ² – 8x – 3 = 0

Solution

3x ² – 9x + x – 3 = 0

⟹ 3x (x – 3) + 1(x – 3) = 0

⟹ (x – 3) (3x + 1) = 0

⟹ x = 3 or x = -13

Example 3

Solve the following quadratic equation (2x – 3)² = 25

Solution

Expand the equation (2x – 3)² = 25 to get;

⟹ 4x ² – 12x + 9 – 25 = 0

⟹ 4x ² – 12x – 16 = 0

Divide each term by 4 to get;

⟹ x ² – 3x – 4 = 0

⟹ (x – 4) (x + 1) = 0

⟹ x = 4 or x = -1

The are many methods of factorizing quadratic equations. In this article, our emphasis will be based on how to factor quadratic equations, in which the coefficient of x² is either 1 or greater than 1.

Therefore, we will use the trial and error method to get the right factors for the given quadratic equation.

Factoring when the Coefficient of x ² is 1

To factorize a quadratic equation of the form x ² + bx + c, the leading coefficient is 1. You need to identify two numbers whose product and sum are c and b, respectively.

CASE 1: When b and c are both positive

Example 4

Solve the quadratic equation: x² + 7x + 10 = 0

List down the factors of 10:

1 × 10, 2 × 5

Identify two factors with a product of 10 and a sum of 7:

1 + 10 ≠ 7
2 + 5 = 7.

Verify the factors using the distributive property of multiplication.

(x + 2) (x + 5) = x² + 5x + 2x + 10 = x² + 7x + 10

The factors of the quadratic equation are:(x + 2) (x + 5)

Equating each factor to zero gives;

x + 2 = 0 ⟹x= -2

x + 5 = 0 ⟹ x = -5

Therefore, the solution is x = – 2, x = – 5

Example 5

x ² + 10x + 25.

Solution

Identify two factors with the product of 25 and sum of 10.

5 × 5 = 25, and 5 + 5 = 10

Verify the factors.

x ² + 10x + 25 = x ² + 5x + 5x + 25

= x (x + 5) + 5x + 25

= x (x + 5) + 5(x + 5)

= (x + 5) (x + 5)

Therefore, x = -5 is the answer.

CASE 2: When b is positive and c is negative

Example 6

Solve x² + 4x – 5 = 0

Solution

Write the factors of -5.

1 × –5, –1 × 5

Identify the factors whose product is – 5 and sum is 4.

1 – 5 ≠ 4
–1 + 5 = 4

Verify the factors using the distributive property.

(x – 1) (x + 5) = x² + 5x – x – 5 = x² + 4x – 5
(x – 1) (x + 5) = 0

x – 1 = 0 ⇒ x = 1, or
x + 5 = 0 ⇒ x = -5

Therefore, x = 1, x = -5 are the solutions.

CASE 3: When b and c are both negative

Example 7

x² – 5x – 6

Solution

Write down the factors of – 6:

1 × –6, –1 × 6, 2 × –3, –2 × 3

Now identify factors whose product is -6 and sum is –5:

1 + (–6) = –5

Check the factors using the distributive property.

(x + 1) (x – 6) = x² – 6 x + x – 6 = x² – 5x – 6

Equate each factor to zero and solve to get;
(x + 1) (x – 6) = 0

x + 1 = 0 ⇒ x = -1, or
x – 6 = 0 ⇒ x = 6

Therefore, the solution is x=6, x = -1

CASE 4: When b is negative and c is positive

Example 8

x² – 6x + 8 = 0

Solution

Write down all factors of 8.

–1 × – 8, –2 × –4

Identify factors whose product is 8 and sum is -6
–1 + (–8) ≠ –6
–2 + (–4) = –6

Check the factors using the distributive property.

(x – 2) (x – 4) = x² – 4 x – 2x + 8 = x² – 6x + 8

Now equate each factor to zero and solve the expression to get;

(x – 2) (x – 4) = 0

x – 2 = 0 ⇒ x = 2, or
x – 4 = 0 ⇒ x = 4

Example 9

Factorize x² +8x+12.

Solution

Write down the factors of 12;

12 = 2 × 6 or = 4 × 3
Find factors whose sum is 8:

2 + 6 = 8
2 × 6 ≠ 8

Use distributive property to check the factors;

= x²+ 6x +2x + 12 = (x²+ 6x) +(2x + 12) = x(x+6) +2(x+6)

= x (x + 6) +2 (x + 6) = (x + 6) (x + 2)

Equate each factor to zero to get;

(x + 6) (x + 2)

x = -6, -2

Factoring when the coefficient of x ² is greater than 1

Sometimes, the leading coefficient of a quadratic equation may be greater than 1. In this case, we can not solve the quadratic equation by the use of common factors.

Therefore, we need to consider the coefficient of x² and the factors of c to find numbers whose sum is b.

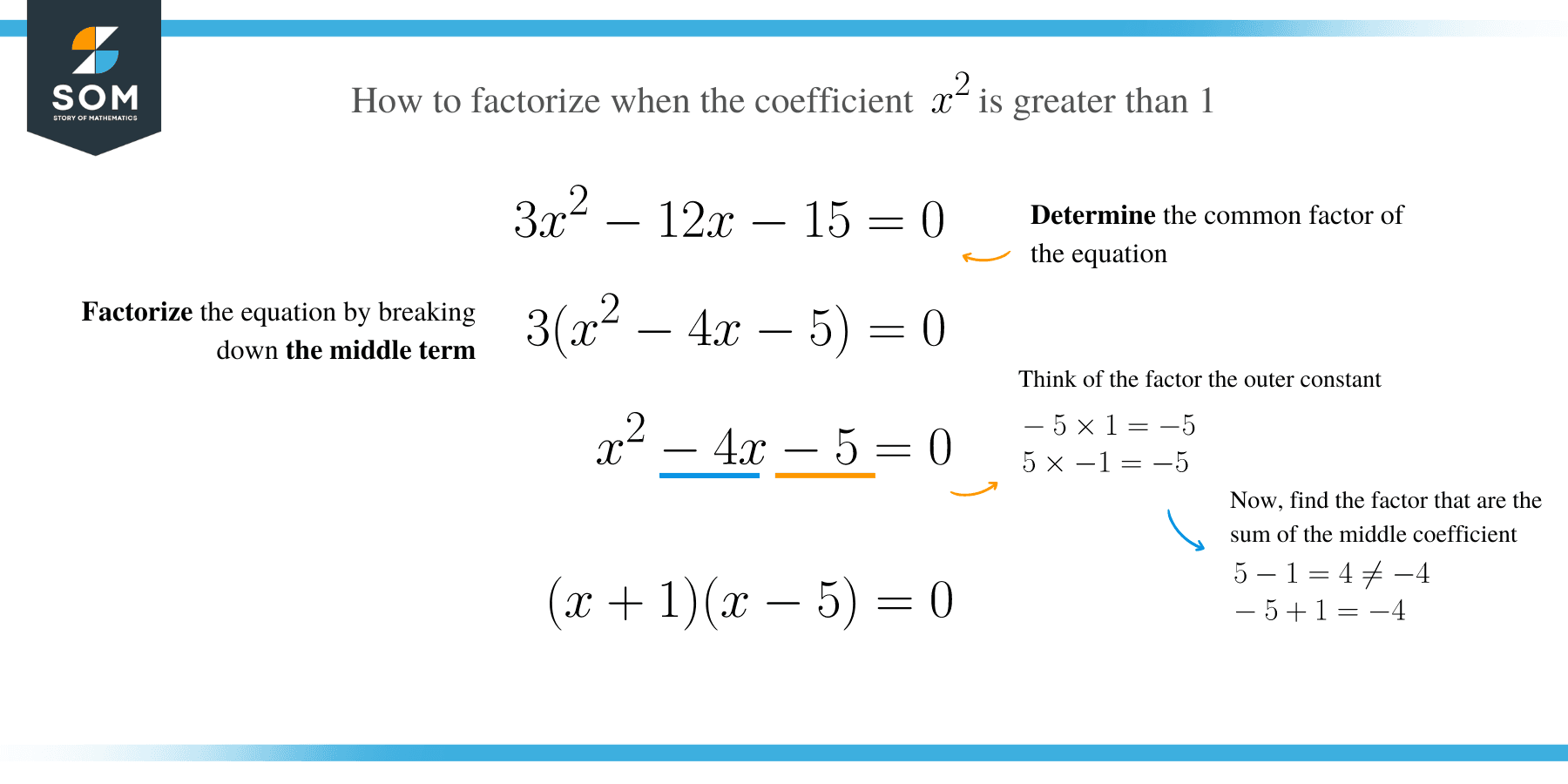
Example 10

Solve 2x² – 14x + 20 = 0

Solution

Determine the common factors of the equation.

2x² – 14x + 20 ⇒ 2(x² – 7x + 10)

Now we can find the factors of (x² – 7x + 10). Therefore, write down factors of 10:

–1 × –10, –2 × –5

Identify factors whose sum is – 7:

1 + (–10) ≠ –7
–2 + (–5) = –7

Check the factors by applying distributive property.

2(x – 2) (x – 5) = 2(x² – 5 x – 2x + 10)
= 2(x² – 7x + 10) = 2x² – 14x + 20

Equate each factor to zero and solve;
2(x – 2) (x – 5) = 0

x – 2 = 0 ⇒ x = 2, or
x – 5 = 0 ⇒ x = 5

Example 11

Solve 7x² + 18x + 11 = 0

Solution

Write down the factors of both 7 and 11.

7 = 1 × 7

11 = 1 × 11

Apply distributive property to check the factors as shown below:

(7x + 1) (x + 11) ≠ 7x² + 18x + 11

(7x + 11) (x + 1) = 7x² + 7x + 11x + 11 = 7x² + 18x + 11

Now equate each factor to zero and solve to get;

7x² + 18x + 11= 0
(7x + 11) (x + 1) = 0

x = -1, -11/7

Example 12

Solve 2x² − 7x + 6 = 3

Solution

2x² − 7x + 3 = 0

(2x − 1) (x − 3) = 0

x=1/2​ or x=3

Example 13

Solve 9x ² +6x+1=0

Solution

Factorize to give:

(3x + 1) (3x + 1) = 0

(3x + 1) = 0,

Therefore, x = −1​/3

Example 14

Factorize 6x²– 7x + 2 = 0

Solution

6x² – 4x – 3x + 2 = 0

Factorize the expression;

⟹ 2x (3x – 2) – 1(3x – 2) = 0

⟹ (3x – 2) (2x – 1) = 0

⟹ 3x – 2 = 0 or 2x – 1 = 0

⟹ 3x = 2 or 2x = 1

⟹ x = 2/3 or x = ½

Example 15

Factorize x² + (4 – 3y) x – 12y = 0

Solution

Expand the equation;

x² + 4x – 3xy – 12y = 0

Factorize;

⟹ x (x + 4) – 3y (x + 4) = 0

x + 4) (x – 3y) = 0

⟹ x + 4 = 0 or x – 3y = 0

⟹ x = -4 or x = 3y

Thus, x = -4 or x = 3y