Frequency Statistic – Explanation & Examples

Frequency, in general means the number of times a certain event has taken place. It can simply be defined as the count of certain event which has occurred.

For example, Let us consider a person Mr.Smith who eats 3 times a day then the frequency of Mr.Smith eating food daily is 3. In this case, we got the value of frequency just by looking at the given statement. But in statistics and real world scenarios, we will have to go through the data and count the number of times an event has occurred and record it in a frequency distribution table.

It might be intimidating for you if you are hearing the term frequency distribution for the first time. But be with me for a while and I will walk you through the entire process in a step by step manner and I can assure you that you not only can understand frequency better but you also can be able to explain it to your friends and family.

So let us get started!

First of all, to know frequency we need to have data. The data can be as simple as a number series.

 Look at the below number series. Let us calculate the frequency of each of these numbers.

1, 2, 3, 2, 4, 5, 6, 2, 2, 1

Here as you can see the number 2 has occurred 4 times in the series as shown below.

1, 2, 3, 2, 4, 5, 6, 2, 2, 1

Hence, frequency of the number 2 is 4.

Similarly, the number 1 has occurred 2 times, the numbers 3, 4, 5 and 6 all have just occurred 1 time as shown below.

1, 2, 3, 2, 4, 5, 6, 2, 2, 1

Frequency of the number 1 is 2.

1, 2, 3, 2, 4, 5, 6, 2, 2, 1

Frequency of the number 3 is 1.

1, 2, 3, 2, 4, 5, 6, 2, 2, 1

Frequency of the number 4 is 1.

1, 2, 3, 2, 4, 5, 6, 2, 2, 1

Frequency of the number 5 is 1.

1, 2, 3, 2, 4, 5, 6, 2, 2, 1

Frequency of the number 6 is 1.

So, as we have got the frequencies of each of the numbers in the given number series we can now construct the frequency distribution table which is as follows.

We have just taken each of unique number in the given number series in the left column and their respective frequencies in the right column. Hence, this table is called a Frequency distribution table. So, we just have learnt how to construct a frequency distribution table‼

This might have given you some basic level of understanding frequency. Let us now go and check out the mathematical definition for frequency.

What is frequency in statistics?

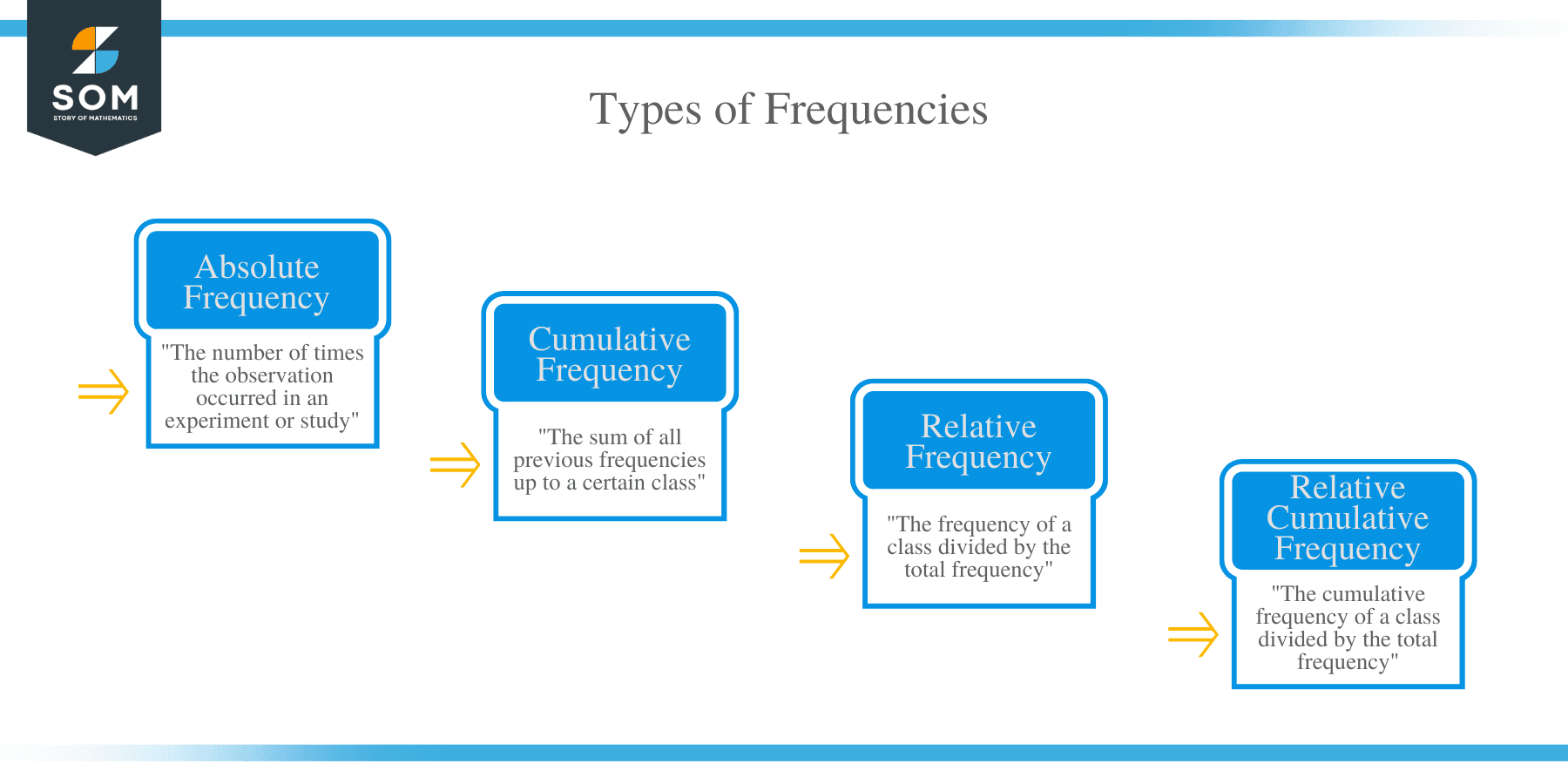
In statistics, frequency of an event is defined as the number of times the observation occurred in an experiment or study. Frequency can otherwise be called as Absolute frequency.

For example, an experiment can be to find out how often it rains on a particular day. Suppose it rains 5 times on this particular day then the frequency of rain on this particular day is 5. In this example, the frequency statistic is the frequency of rain on this particular day and the value of this frequency is 5.

How do you find the frequency in statistics?

Previously, we have found frequency of different numbers in a given number series previously. Suppose, we want to know how many times a student scored the highest in a class test conducted on 9 consecutive days and we have the names of the students who scored the highest on each particular day as follows.

Harris, Jarvis, Aldo, Boris, Aldo, Jarvis, Boris, Boris, Aldo.

We can do this by simply counting the number of times a student’s name has occurred in the above list. So, let us now find out the frequency of each of the given names as we did in the case of numbers.

• What is the frequency of the name Harris?

Harris, Jarvis, Aldo, Boris, Aldo, Jarvis, Boris, Boris, Aldo.

The answer is 1.

• What is the frequency of the name Jarvis?

Harris, Jarvis, Aldo, Boris, Aldo, Jarvis, Boris, Boris, Aldo.

The answer is 2.

• What is the frequency of the name Aldo?

Harris, Jarvis, Aldo, Boris, Aldo, Jarvis, Boris, Boris, Aldo.

The answer is 3.

• What is the frequency of the name Boris?

Harris, Jarvis, Aldo, Boris, Aldo, Jarvis, Boris, Boris, Aldo.

The answer is 3.

By calculating the frequency for each of the names we have indirectly contributed in constructing a frequency distribution table. But before showing you the frequency distribution table, let us briefly go through what is a frequency distribution table mathematically.

A table that displays the frequency of various outcomes in a sample is called a Frequency distribution table.

The Frequency distribution table for the problem we solved is as below.

Harris, Jarvis, Aldo, Boris, Aldo, Jarvis, Boris, Boris, Aldo.

Remember, the frequency that we calculated in the above 2 examples can be called as absolute frequency as well.

Let us now go through different types of frequencies.

Types of Frequencies

Now that you have got a good understanding of frequency, let us look into the different types of frequencies and add each of this frequency to our frequency distribution table.

The types of frequencies are broadly classified into

• Absolute Frequency (the frequency we discussed so far J)
• Cumulative Frequency
• Relative Frequency
• Relative cumulative frequency

Let us go through each of the types in detail.

Cumulative Frequency

Cumulative frequency is the sum of all previous frequencies up to a certain class. Let us now calculate cumulative frequency for our problem.

• The cumulative frequency for the name Harris is 1 i.e., the current frequency itself as there are no previous frequencies.
• The cumulative frequency for the name Jarvis is 3 (2 + 1) i.e., the sum of current frequency for the name Jarvis and the previous frequency for the name Harris.
• The cumulative frequency for the name Aldo is 6 (3 + 3) i.e., the sum of current frequency for the name Aldo and the previous cumulative frequency.
• The cumulative frequency for the name Boris is 6 (3 + 6) i.e., the sum of current frequency for the name Boris and the previous cumulative frequency.

Now the total frequency for this problem is 9. Remember this, as this will be used later. J

Just to give you a little understanding on what total frequency is, here is its brief definition. Total frequency is defined as the sum of all the frequencies in the frequency distribution table.

Relative Frequency

The frequency of a class divided by the total frequency is called the Relative frequency of a particular class. Let us now calculate relative frequency for our problem and don’t forget the total frequency value of 9 which we calculated earlier. 

 The relative frequency for the name Harris is the frequency of the name Harris divided by the total frequency i.e., 1/9.

• The relative frequency for the name Jarvis is the frequency of the name Jarvis divided by the total frequency i.e., 2/9.
• The relative frequency for the name Aldo is the frequency of the name Jarvis divided by the total frequency i.e., 3/9 which is equal to 1/3.
• The relative frequency for the name Boris is the frequency of the name Boris divided by the total frequency i.e., 3/9 which is equal to 1/3.

Relative Cumulative Frequency

The cumulative frequency of a class divided by the total frequency is called the Relative Cumulative frequency of a particular class.

• The relative cumulative frequency for the name Harris is the cumulative frequency of the name Harris divided by the total frequency i.e., 1/9.
• The relative cumulative frequency for the name Jarvis is the cumulative frequency of the name Jarvis divided by the total frequency i.e., 3/9 which is equal to 1/3.
• The relative cumulative frequency for the name Aldo is the cumulative frequency of the name Jarvis divided by the total frequency i.e., 6/9 which is equal to 2/3.
• The relative cumulative frequency for the name Boris is the cumulative frequency of the name Boris divided by the total frequency i.e., 9/9 which is equal to 1.

Another important information you need to know is that Relative Cumulative Frequency can be also referred to as Percentage Frequency but the only difference is the result is multiplied by a factor 100 to be represented in percentage and hence the name Percentage Frequency.

The percentage frequency for the names is calculated as follows.

• The percentage frequency for the name Harris is the relative cumulative frequency of the name Harris multiplied by 100 i.e., 1/9 × 100 which is equal to 11.11%.
• The percentage frequency for the name Jarvis is the cumulative frequency of the name Jarvis divided by the total frequency i.e., 3/9 × 100 which is equal to 33.33%.
• The percentage frequency for the name Aldo is the cumulative frequency of the name Jarvis divided by the total frequency i.e., 2/3 × 100 which is equal to 66.67%.
• The percentage frequency for the name Boris is the cumulative frequency of the name Boris divided by the total frequency i.e., 1 × 100 which is equal to 100%.

Conclusion

In this article we have discussed about the following.

1. Frequency is nothing but how often an event has occurred.
2. A Frequency Distribution Table is the table which displays the frequency of various outcomes for a given sample.
3. Frequency is also called as Absolute Frequency.
4. Cumulative Frequency is the value obtained by adding up all the previous frequencies up to a certain class.
5. Total Frequency is the value obtained by adding up all the frequencies in the frequency distribution table.
6. Relative Frequency is the value obtained by dividing the absolute frequency by the total frequency.
7. Relative Cumulative Frequency is the value obtained by the cumulative frequency by the total frequency.
8. Percentage Frequency is the value obtained by multiplying 100 to the relative cumulative frequency.

Previous Lesson | Main Page | Next Lesson