- Home
- >
- Fundamental Theorem of Calculus – Parts, Application, and Examples
JUMP TO TOPIC
Fundamental Theorem of Calculus – Parts, Application, and Examples
 From its name, the Fundamental Theorem of Calculus contains the most essential and most used rule in both differential and integral calculus. This theorem contains two parts – which we’ll cover extensively in this section.
From its name, the Fundamental Theorem of Calculus contains the most essential and most used rule in both differential and integral calculus. This theorem contains two parts – which we’ll cover extensively in this section.
The new techniques we’ll be learning depend on the idea that both differentiation and integration are related to each other. During the 1600s and 1700s, understanding this relationship has piqued the interest of many mathematicians including Sir Isaac Newton and Gottfried Leibniz. These two parts are now what we know as the Fundamental Theorem of Calculus.
The Fundamental Theorem of Calculus shows us how differentiation and differentiation are closely related to each other. In fact, these two are other’s inverses. This theorem also tells us how
In this article, we’ll explore the two major points covered by the Fundamental Theorem of Calculus (or FTC).
- The first part of the fundamental theorem shows us how the function’s derivative and integral are related to each other.
- The second part of the fundamental theorem shows us how to evaluate definite integrals using our knowledge of antiderivative
- We’ll also show you how the two parts of the fundamental theorem of calculus were derived.
Let’s begin by understanding the two main parts of the fundamental theorem of calculus. We’ll use these concepts to eventually solve different types of exercises and word problems. As we have mentioned, this is going to be a thorough discussion of the FTC, so make sure to take notes and keep your previous resources handy.
What is the fundamental theorem of calculus?
The fundamental theorem of calculus (we’ll reference it as FTC every now and then) shows us the formula that showcases the relationship between the derivative and integral of a given function.
The fundamental theorem of calculus contains two parts:
- The first part of the fundamental theorem of calculus tells us that when we have $F(x) =\int_{a}^{x} f(t)\phantom{x}dt$, $a\leq x\leq b$, $F(x)$ is the antiderivative of $f$. This extends to the fact that $\dfrac{d}{dx}\left(\int_{a}^{x} f(t)\phantom{x}dt\right) =F(x)$ or $F^{\prime}(x) = f(x)$
- The second fundamental theorem of calculus shows us if $F(x)$ is the antiderivative of $f(x)$ then we have $\int_{a}^{b} f(x)\phantom{x} dx = F(b) – F(a)$.
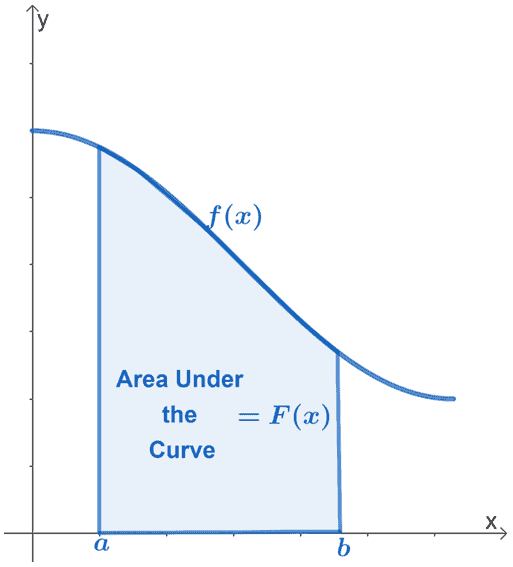
These two theorems help us address important problems in Calculus such as:
- Finding the area under the curve of a function – that includes areas under a parabola or a circle.
- Developing a strategy to find the instantaneous rate of change of a given function’s slope at any point.
By the end of this discussion, the graph shown above will make more sense. We will understand how we can use $f(x)$ to find the area under its curve from the interval, $a \leq x \leq b$. For now, let’s focus on understanding the significance of the two fundamental theorem of calculus. We’ll also learn how to apply them for different expressions and situations.
Understanding the first fundamental theorem of calculus
The first part of the fundamental theorem of calculus establishes the relationship between differentiation and integration. If $f(x)$ is continuous throughout the interval, $[a, b]$, we can define the function, $F(x)$ as:
\begin{aligned}F(x) &= \int_{x}^{a}f(t)\phantom{x}dt \end{aligned}
This confirms the fact that $F(x)$ is indeed $f(x)$’s antiderivative over the interval, $[a, b]$.
\begin{aligned}F^{\prime}(x) &= f(x) \end{aligned}
These two equations tell us that $F(x)$ is the definite integral of $f(x)$ throughout the interval, $[a, b]$. This also extends the fact that the definite integral returns a constant. We’ve also shown how we can relate the derivative and integral of a given function: integration is the opposite of differentiation.
\begin{aligned}\dfrac{d}{dx}\int_{a}^{x} f(t)\phantom{x}dt &= f(x) \end{aligned}
This is Leibniz notation of the first fundamental theorem. Now, how do we apply this theorem?
Let’s say we want to determine the derivative of $g(x) = \int_{3}^{x} (3^t + t)\phantom{x}dt$, we can find $g^{\prime}(x)$ using the first fundamental theorem of calculus.
Since the function, $3^t +t$, is continuous, through the first fundamental theorem, we can immediately conclude that $g^{\prime}(x) = 3^x + x$.
Here are some more examples that can help you understand the first fundamental theorem of calculus:
| Integration | Differentiation |
| \begin{aligned} j(t) = \int_{6}^{x} (4t + 1)\phantom{x}dt \end{aligned} | \begin{aligned} j^{\prime}(x) = 4x + 1\end{aligned} |
| \begin{aligned} k(r) = \int_{8}^{x} (\sqrt{r} – 1)\phantom{x}dr \end{aligned} | \begin{aligned} k^{\prime}(x) = \sqrt{x} -1\end{aligned} |
| \begin{aligned} l(t) = \int_{2}^{x} \dfrac{1}{t^2 – 2t + 1}\phantom{x}dt \end{aligned} | \begin{aligned} l^{\prime}(x) = \dfrac{1}{x^2 – 2x + 1}\end{aligned} |
We can extend this rule further by using the chain rule. This occurs when the upper limit is a function of $x$ too. If we have a differentiable function, $h(x)$, we have the definite integral shown below:
\begin{aligned}\dfrac{d}{dx}\int_{a}^{h(x)} f(t)\phantom{x}dt &=f[h(x)] \cdot \dfrac{d}{dx}h(x)\end{aligned}
This means that $f^{\prime}(x) = f[h(x)] \cdot h^{\prime}(x)$. Let’s say we want to find $F^{\prime}(x)$ given the definite integral, $F(x) = \int_{0}^{x^3} \cos t\phantom{x}dt$. Find $F^{\prime}(x)$’s expression using the first theorem and the chain rule.
\begin{aligned}F^{\prime}(x)&=\dfrac{d}{dx}\int_{0}^{x^3} \cos t\phantom{x}dt \\&= \cos(x^4)\cdot \dfrac{d}{dx}(x^3)\\&= \cos(x^3) \cdot {\color{Teal}(3x^2)},\phantom{x}{\color{Teal}\text{Power Rule}}\\&= 3x^2\cos(x^3)\end{aligned}
Hence, we have $F^{\prime}(x) = 3x^2\cos(x^3)$ and this confirms how it’s possible to use the antiderivative and chain rule to find $F^{\prime}(x)$.
The first fundamental theorem establishes the idea that integration is simply the opposite of differentiation: when we have $F(x) = \int_{a}^{b} f(x)\phantom{x} dx$, $F(x)$ is the antiderivative of $f(x)$.
Understanding the second fundamental theorem of calculus
The second part of the fundamental theorem of calculus shows us how antiderivatives and definite integrals are related to each other. Let’s say we have a function, $f(x)$, that is continuous throughout the interval, $[a, b]$, we have the following equation when $F(x)$ is the antiderivative of $f(x)$:
\begin{aligned}\int_{a}^{b}f(x)\phantom{x}dx &= F(b) – F(a)\\&= F(x)|_{a}^{b}\end{aligned}
This highlights the definition of definite integrals and the process of finding the value of $\int_{a}^{b}f(x)\phantom{x}dx$.
To find the definite integral of a function for the interval, $[a, b]$, we’ll have to:
- Find the expression for the indefinite integral of the function.
- Evaluate the indefinite integral at $x= a$ and $x= b$.
- Subtract $F(a)$ from $F(b)$. This is also what $ F(x)|_{a}^{b}$ represents.
The second part of the FTC can also be rewritten as shown below.
\begin{aligned}\int_{a}^{b} g^{\prime}(x)\phantom{x}dx &= g(b) – g(a)\end{aligned}
This form clearly highlights how a function’s derivative and antiderivative are related to each other.
This theorem helps us evaluate expressions such as $\int_{4}^{8} -2x^3\phantom{x}dx$. From the second part of $FTC$, we’ll have to find the expression for $\int -2x^3\phantom{x} dx$ first.
- Take the constant out, $\int -2x^3\phantom{x} dx= -2\left(\int x^3\phantom{x} dx\right)$.
- Use the power rule for integral calculus, $\int x^n\phantom{x}dx = \dfrac{x^{n +1}}{n +1} + C$.
\begin{aligned}\int -2x^3\phantom{x}dx &= {\color{Teal}-2}\int x^3\phantom{x}dx,\phantom{x}\color{Teal}\text{Constant Multiple Rule}\\&=-2\left({\color{Teal}\dfrac{x^{3 + 1}}{3 + 1} }\right )+ C\phantom{x}\color{Teal}\text{Power Rule}\\&= -2\cdot \dfrac{x^4}{4}+C\\&=-\dfrac{1}{2}x^4 +C \end{aligned}
Since we’re working with definite integrals, we don’t need to account for the constant,$\boldsymbol{C}$ and we’ll show you why. Through the second part of FTC, we’ll be able to find the exact value of $\int_{4}^{8}-2x^3\phantom{x}dx$.
\begin{aligned}\int_{4}^{8}-2x^3\phantom{x}dx &=-\dfrac{1}{2}x^4 +C|_{4}^{8}\\&=-\dfrac{1}{2}[(8)^4 + \cancel{C}- (4)^4 -\cancel{C}]\\&= -1920\end{aligned}
This confirms that definite integrals will return an exact value.
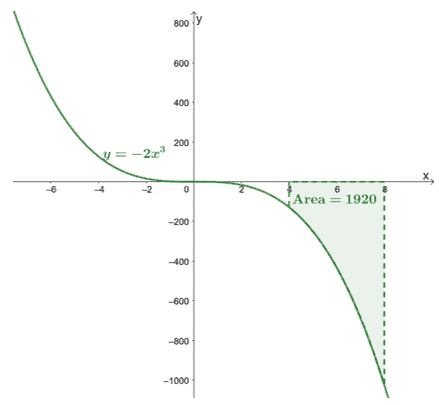
Here’s the graph of $y =- 2x^3$ and we’ve included the area of the curve bound by $[4, 8]$ and the $x$-axis. The area is simply the absolute value of $\int_{4}^{8}-2x^3\phantom{x}dx$.
This shows that we can find the area under the curve of $\boldsymbol{f(x)}$ within a given interval, $[a, b]$, by evaluating its definite integral,$\boldsymbol{\int_{a}^{b} f(x)\phantom{x}dx}$.
Here’s a list of important properties you’ll need when evaluating a function’s definite properties:
| Properties of Definite Integrals | |
| Sum or Difference | $\int_{a}^{b} [f(x) \pm g(x)]\phantom{x}dx = \int_{a}^{b} f(x) \phantom{x}dx \pm \int_{a}^{b} g(x) \phantom{x}dx $ |
| Constant Multiple | $\int_{a}^{b} [k\cdot f(x)]\phantom{x}dx = k\int_{a}^{b} f(x) \phantom{x}dx$ |
| Reverse Interval | $\int_{a}^{b} f(x)\phantom{x}dx = -\int_{b}^{a} f(x) \phantom{x}dx$ |
| Zero-length Interval | $\int_{a}^{a} f(x)\phantom{x}dx = 0$ |
| Combining Intervals | $\int_{a}^{b} f(x)\phantom{x}dx + \int_{b}^{c} f(x)\phantom{x}dx = \int_{a}^{c} f(x)\phantom{x}dx$ |
Apply these properties whenever needed to simplify and evaluate definite integrals.
How to prove the fundamental theorem of calculus?
Now that we have covered the two parts of the fundamental theorem of calculus, it’s time that we learn how these theorems were established.
- We’ll be using the formal definition of derivatives to rewrite the derivative of $F(x) =\int_{a}^{x} f(t) \phantom{x} dt$. With the help of the Mean Value Theorem, we’ll be able to show that $F^{\prime}(x) = f(x)$.
- After proving the first part of the fundamental theorem of calculus, use this to prove the second half of the FTC. We’ll then be able to prove that when $F(x)$ is the antiderivative of $f(x)$, we have the definite integral, $\int_{a}^{b}f(x)\phantom{x}dx = F(b) – F(a)$.
Since the Mean Value Theorem (MVT) is essential in proving both parts of the fundamental theorem of calculus, it’s best that we discuss this first before showing you the proofs of the two parts.
Mean Value Theorem for Derivatives
We’ve already covered the mean value theorem for differential calculus. According to the mean value theorem, if $f(x)$ is a continuous and differentiable function over the interval, $(a, b)$, a secant line passes through the point, $(c, f(c))$, where $c \in (a, b)$. This secant line will be parallel to two tangent lines passing through $f(x)$.
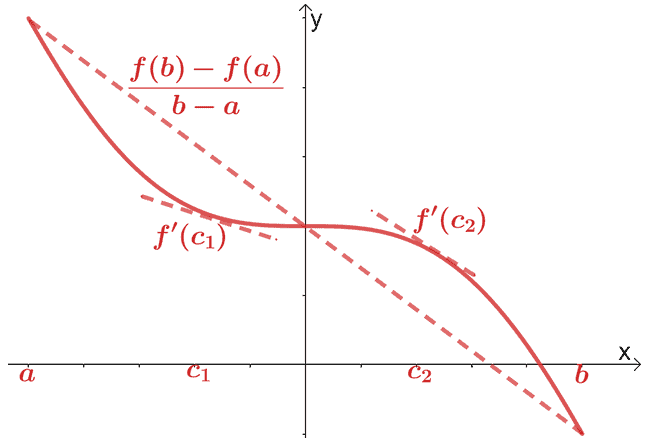
Mathematically, we have the relationship shown below:
\begin{aligned}f^{\prime}(c) &= \dfrac{f(b) – f(a)}{b – a}\end{aligned}
We can extend this theorem and have the following properties:
- Property 1: When $f^{\prime}(x) = 0$ for all $x$ in the interval, $(a, b)$, this means that $f(x)$ is constant throughout $(a, b)$.
- Property 2: When $f^{\prime}(x) = g^{\prime}(x)$ for all $x$ in the interval, $(a, b)$, we have $f(x) = g(x) + c$, where $c$ is a constant.
Mean Value Theorem for Integrals
The mean value theorem for integrals states that when $f(x)$ is continuous, there exists a point, $c$, between the interval, $[a, b]$, where $\boldsymbol{f(c)}$ is equal to $\boldsymbol{f(x)}$’s average value throughout the interval.
Mathematically, when we have a continuous function, $f(x)$, for the interval, $[a, b]$, there is a point, $c \in [a, b]$, where it satisfies the equation shown below:
\begin{aligned}f(c) &= \dfrac{1}{b -a} \int_{a}^{b} f(x)\phantom{x}dx\\\int_{a}^{b} f(x)\phantom{x}dx &= f(c)(b -a)\end{aligned}
Let’s say when we have $f(x) = 6 -3x$ over the interval, $[0, 2]$. We can find the average value of $f(x)$ over the interval, $[0,2]$.
\begin{aligned}\text{Average Value}&= \dfrac{1}{2 -0} \int_{0}^{2} (6 – 3x)\phantom{x}dx\\&=\dfrac{1}{2}\left[\left(\int_{0}^{2} 6\phantom{x}dx\right )- \left(\int_{0}^{2} 3x\phantom{x}dx\right ) \right ]\\&= \dfrac{1}{2}\left[\left( \dfrac{6x^{0 + 1}}{0 +1}\right )|_{0}^{2} -\left( \dfrac{3x^{1+ 1}}{1 +1}\right )|_{0}^{2}\right ]\\&= \dfrac{1}{2}\left[6(x|_{0}^{2} )- \dfrac{3}{2}(x^2|_{0}^{2})\right]\\&= \dfrac{1}{2}\left[6(2- 0) – \dfrac{3}{2}(2^2 – 0^2)\right]\\&= 3 \end{aligned}
We can also find the value of $x$ where $f(x) = 3$.
\begin{aligned} 6- 3x &= 3\\-3x &= -3\\x&= 1\end{aligned}
This means that the average value of $f(x)$ is $3$ and this occurs when $x = 1$.
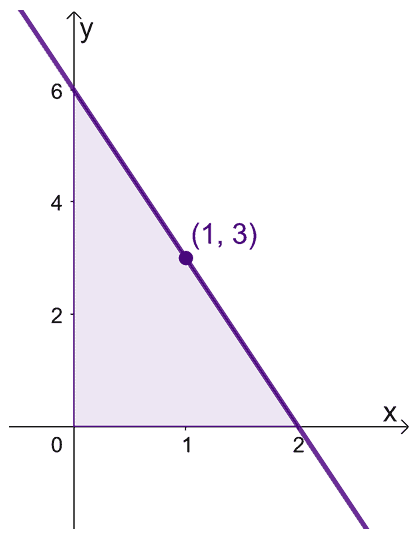
This shows that there is indeed a value within the interval, $[0, 2]$, where $f(x)$ reflects its average value. Keep this theorem in mind when we’re manipulating our expressions for the two proofs shown below.
Proof of the first fundamental theorem of calculus
Let’s begin by rewriting $F^{\prime}(x)$ in terms of limits as shown below.
\begin{aligned}F^{\prime}(x) &= \lim_{h \rightarrow 0} \dfrac{F(x + h) – F(x)}{h}\end{aligned}
Factor our $\dfrac{1}{h}$ and rewrite $F(x + h)$ and $F(x)$ as their integral expressions.
\begin{aligned}F^{\prime}(x) &= \lim_{h \rightarrow 0}\dfrac{1}{h} [F(x + h) – F(x)]\\&=\lim_{h \rightarrow 0}\dfrac{1}{h}\left[\int_{a}^{x + h} f(t) dt -\int_{x}^{a} f(t) dt\right ]\\&= \lim_{h \rightarrow 0}\dfrac{1}{h}\left[{\color{Teal}\int_{x}^{x + h} f(t) dt }\right ],\phantom{x}\color{Teal}\text{Combining Intervals} \end{aligned}
If you take a look at the last expression and using the mean value theorem for integrals, this is simply equivalent to the average value of $f(x)$ over the interval, $[x, x+ h]$.
\begin{aligned}\dfrac{1}{h}\lim_{h \rightarrow 0}\int_{x}^{x + h} f(t)&=\dfrac{1}{h}\lim_{h \rightarrow 0}\int_{x}^{x + h} f(x)\phantom{x}dx \\&= f(c)\end{aligned}
Keep in mind that $h \in [x, x+ h]$, so $c \rightarrow x$ when $h \rightarrow 0$.
\begin{aligned}\lim_{h \rightarrow 0}f(c) &= \lim_{c \rightarrow x} f(x)\\&= f(x)\end{aligned}
We can now go back to the last expression for $F^{\prime}(x)$ and use the two properties we’ve just established.
\begin{aligned}F^{\prime}(x)&= \lim_{h \rightarrow 0}\dfrac{1}{h}\int_{x}^{x + h} f(t) dt \\&= \lim_{h \rightarrow 0} f(c)\\&= f(x)\end{aligned}
Hence, we’ve proven the first fundamental theorem of calculus: that when we have $F(x) = \int_{a}^{x} f(t)\phantom{x}dt$, we have $F^{\prime}(x) = f(x)$.
Proof of the second fundamental theorem of calculus
Let’s say we have $g(x) = \int_{a}^{b}f(t)\phantom{x}dt$, so using the first part of the fundamental theorem of calculus, $g^{\prime}(x) = f(x)$. This also means that $g(x)$ is an antiderivative of $f(x)$ over the interval, $[a, b]$.
If we let $F(x)$ represent any antiderivative (this means only the constant, $C$ will vary) of $f(x)$ throughout $[a, b]$,we have the following:
\begin{aligned}g^{\prime}(x) &= F^{\prime}(x)\end{aligned}
Use the second property of the MVT, we have $F(x) = g(x) + c$. This means that for $a\leq x \leq b$ and $F(x) = g(x) + c$, we have the relationship shown below.
\begin{aligned}F(b) – F(a) &= [g(b) + c] – [g(a) +c]\\&=g(b) – g(a) \end{aligned}
Rewrite this expression using the initial definition we have for $g(x)$.
\begin{aligned}g(t) &= \int_{a}^{x} f(t)\phantom{x}dt\\\\g(b) – g(a)&= \int_{a}^{b}f(b)\phantom{x}dt – \int_{a}^{a}f(a)\phantom{x}dt\\&= \int_{a}^{b}f(b)\phantom{x}dt – {\color{Teal}0},\phantom{x}\color{Teal}\text{Zero-length Interval}\\&= \int_{a}^{b}f(t)\phantom{x}d\end{aligned}
We can swap the variable $t$ with $x$, hence we have the following:
\begin{aligned}F(b) – F(a) &= \int_{a}^{b}f(x)\phantom{x}dx\\ \int_{a}^{b}f(x)\phantom{x}dx &= F(b) – F(a)\end{aligned}
This shows that the second part of the fundamental theorem of calculus is true. Now that we know the theories and properties used to prove the two parts of the FTC, it’s time that we apply the actual theories. We’ve prepared an extensive range of problems for you to work on and make sure that you master the two essential concepts we’ve just discussed.
Example 1
Differentiate the following expressions.
a. $f(x)= \int_{3}^{x} e^{t^3}\phantom{x} dt$
b. $g(x)= \int_{-6}^{x} \sqrt[4]{4 – t^2}\phantom{x} dt$
c. $h(x)= \int_{1}^{x^2} \sin t\phantom{x} dt$
Solution
According to the first part of the fundamental theorem of calculus, we have $\dfrac{d}{dx}\int_{a}^{x} f(t)\phantom{x}dt = f(x)$. This means that the derivative of $ \int_{a}^{x} f(t)$ is simply equal to $f(t)$ evaluated at the upper limit.
For the first function, we have $f(x)= \int_{3}^{x} e^{t^3}\phantom{x} dt$, so we’ll use the first part of the FTC to evaluate $f^{\prime}(x)$.
\begin{aligned}f^{\prime}(x)&= \dfrac{d}{dx}\int_{3}^{x} e^{t^3}\phantom{x} dt\\&=e^{t^3},\phantom{x}\color{Teal}\text{where }t = x\\&= e^{x^3} \end{aligned}
We’ll apply a similar process to find the expression for $g^{\prime}(x)$.
\begin{aligned}g^{\prime}(x)&= \dfrac{d}{dx}\int_{-6}^{x} \sqrt[4]{4-t^2}\phantom{x} dt\\&=\sqrt[4]{4-t^2},\phantom{x}\color{Teal}\text{where }t = x\\&= \sqrt[4]{4-x^2} \end{aligned}
The third expression is a bit trickier since the upper limit of the integral expression is $x^2$. For this case, we’ll have to account for the chain rule, and use the property, $ \dfrac{d}{dx}\int_{a}^{h(x)} f(t)\phantom{x}dt =f[h(x)] \cdot \dfrac{d}{dx}h(x)$.
\begin{aligned}h^{\prime}(x)&=\dfrac{d}{dx}\int_{1}^{x^2} \sin t\phantom{x}dt \\&= \sin(x^2)\cdot \dfrac{d}{dx}(x^2)\\&= \sin(x^2) \cdot {\color{Teal}(2x^1)},\phantom{x}{\color{Teal}\text{Power Rule}}\\&= 2x\sin(x^2)\end{aligned}
Example 2
Differentiate the following expressions.
a. $f(x)= \int_{3}^{x^4} e^t\phantom{x} dt$
b. $g(x)= \int_{x^2}^{1} \dfrac{t^2 + 1}{t^4 + 4}\phantom{x} dt$
c. $h(x)= \int_{1}^{\sqrt{x} \tan x} 3\ln t\phantom{x} dt$
Solution
Since we have $x^4$ for the upper limit of $f(x)$’s integral part, we’ll also be accounting for the chain rule. Use the first fundamental theorem of calculus, $ \dfrac{d}{dx}\int_{a}^{h(x)} f(t)\phantom{x}dt =f[h(x)] \cdot \dfrac{d}{dx}h(x)$ to find $f^{\prime}(x)$.
\begin{aligned}f^{\prime}(x)&=\dfrac{d}{dx}\int_{3}^{x^4} e^t\phantom{x}dt \\&= e^{(x^4)}\cdot \dfrac{d}{dx}(x^4)\\&= e^{x^4} \cdot {\color{Teal}(4x^3)},\phantom{x}{\color{Teal}\text{Power Rule}}\\&= 4x^3e^{x^4}\end{aligned}
The lower limit has $x^2$ for $g(x)$’s integral part, so we’ll have to flip that upper and lower limits first. To do so, use the reverse integral property, $\int_{a}^{b} f(x)\phantom{x}dx = -\int_{b}^{a} f(x) \phantom{x}dx$.
\begin{aligned}g(x)&= \int_{x^2}^{1} \dfrac{t^2 + 1}{t^4 + 4}\phantom{x} dt\\&= -\int_{1}^{x^2} \dfrac{t^2 + 1}{t^4 + 4}\phantom{x} dt\end{aligned}
Now that we have $x^2$ as the upper limit, apply a similar process to evaluate $\dfrac{d}{dx}g(x)$ as we did for $f^{\prime}(x)$.
\begin{aligned}g^{\prime}(x)&=\dfrac{d}{dx}\left(-\int_{1}^{x^2} \dfrac{t^2 + 1}{t^4 + 4}\phantom{x} dt \right ) \\&=- \dfrac{d}{dx}\left(\int_{1}^{x^2} \dfrac{t^2 + 1}{t^4 + 4}\phantom{x} dt \right )\\&= -\left[\dfrac{(x^2)^2 + 1}{(x^2)^4 + 4} \cdot \dfrac{d}{dx} (x^2) \right ]\\&= -\left[\dfrac{x^4 + 1}{x^8 + 4} \cdot {\color{Teal}(2x^1)} \right ],\phantom{x}{\color{Teal}\text{Power Rule}}\\&= -\dfrac{2x(x^4 + 1)}{x^8 + 4}\end{aligned}
Let’s now work on the third item: $h(x)= \int_{1}^{\sqrt{x} \tan x} 3\ln t\phantom{x} dt$. To find $h^{\prime}(x)$, account for the derivative of $\sqrt{x} \tan x$ and apply the chain rule.
\begin{aligned}\dfrac{d}{dx}(\sqrt{x} \tan x) &= \sqrt{x}\dfrac{d}{dx}\tan x+ \tan x \dfrac{d}{dx}\sqrt{x},\phantom{x}\color{Teal}\text{Product Rule}\\&= \sqrt{x}({\color{Teal}\sec^2x}) + \tan x\left[{\color{Teal}\dfrac{1}{2}(x) ^{\frac{1}{2} -1}}\right ],\phantom{x}\color{Teal}\text{Derivative of tan & Power Rule}\\&= \sqrt{x}\sec^2 x+ \dfrac{\tan x}{2\sqrt{x}} \end{aligned}
Now, let’s go back to finding $h^{\prime}(x)$ and use this new expression for $h^{\prime}(x)$.
\begin{aligned}h^{\prime}(x)&=\dfrac{d}{dx}\int_{1}^{\sqrt{x} \tan x} 3\ln t\phantom{x} dt\\&= 3\ln(\sqrt{x}\tan x)\cdot \dfrac{d}{dx}(\sqrt{x}\tan x)\\&= 3\ln(\sqrt{x}\tan x)\cdot \left(\sqrt{x}\sec^2 x+ \dfrac{\tan x}{2\sqrt{x}} \right )\end{aligned}
Example 3
Evaluate the following definite integrals.
a. $ \int_{1}^{5} 4x^2\phantom{x}dx$
b. $\int_{0}^{6} (2x^2 – 5)\phantom{x}dx$
c. $\int_{a}^{b} x^2\phantom{x}dx$, where $a$ and $b$ are constants
Solution
Use the second part of the fundamental theorem of calculus to evaluate the three definite integrals. Recall that when $F(x)$ is the antiderivative of $f(x)$,we have the following:
\begin{aligned}\int_{a}^{b}f(x)\phantom{x}dx &= F(b) – F(a)\\&= F(x)|_{a}^{b}\end{aligned}
To evaluate the definite integral, $\int_{1}^{5} 4x^2\phantom{x}dx$, let’s first find the integral of $4x^2$.
\begin{aligned}\int 4x^2\phantom{x}dx&= 4\int x^2\phantom{x}dx,\phantom{x}\color{Teal}\text{Constant Multiple Rule} \\&= 4 \left({\color{Teal}\dfrac{x^{2 + 1}}{2 + 1}}\right) + C,\phantom{x}\color{Teal}\text{Power Rule} \\&= \dfrac{4}{3}x^3 + C\end{aligned}
Since $F(x) = \dfrac{4}{3}x^3$ when $f(x) = 4x^2$, we can evaluate the definite integral by finding the difference between $F(1)$ and $F(5)$.
\begin{aligned}\int_{1}^{5}4x^2\phantom{x}dx &=\dfrac{4}{3}x^3|_{1}^{5}\\&=\dfrac{4}{3}[(5)^3 – (1)^3]\\&= \dfrac{4}{3}(124)\\&= \dfrac{496}{3}\end{aligned}
This means that $\int_{1}^{5} 4x^2\phantom{x}dx = \dfrac{496}{3}$.
Apply a similar approach when evaluating the definite integral, $\int_{0}^{6} (2x^2 – 5)\phantom{x}dx$.
\begin{aligned}\int(2x^2 – 5)\phantom{x}dx&=\int2x^2 \phantom{x}dx-\int 5 \phantom{x}dx,\phantom{x}\color{Teal}\text{Sum Rule}\\&={\color{Teal}2\int x^2 \phantom{x}dx}-{\color{Orchid}(5x + C)},\phantom{x}{\color{Teal}\text{Constant Multiple Rule}}\text{ & }{\color{Orchid}\text{Constant Rule }}\\&= 2\left({\color{Teal}\dfrac{x^{2 +1}}{2 + 1}} \right ) – 5x + C,\phantom{x}{\color{Teal}\text{Power Rule}}\\&=\dfrac{2}{3}x^3 – 5x+C \end{aligned}
Let’s now evaluate the antiderivative at the upper and lower limits of the definite integral.
\begin{aligned}\int_{0}^{6}(2x^2 – 5)\phantom{x}dx&=\dfrac{2}{3}x^3 – 5x |_{0}^{6}\\&= \left[\left(\dfrac{2}{3}\cdot 6^3 – 5\cdot 6\right ) -\left(\dfrac{2}{3}\cdot 0^3 – 5\cdot 0\right )\right]\\&= 144 – 30\\&= 114 \end{aligned}
Hence, we have $\int_{0}^{6} (2x^2 – 5)\phantom{x}dx = 114$.
For the third integral, treat $\int_{a}^{b} x^2\phantom{x}dx$’s upper and lower limits as constants. Once we have the antiderivative of $\int x^2\phantom{x}dx$, evaluate this at $x=a$ and $x=b$.
\begin{aligned}\int x^2\phantom{x}dx&= {\color{Teal}\dfrac{x^{2 + 1}}{2 + 1}} + C,\phantom{x}\color{Teal}\text{Power Rule} \\&= \dfrac{1}{3}x^3 + C\\\\\int_{a}^{b} x^2\phantom{x}dx&= \dfrac{1}{3}x^3|_{a}^{b}\\&= \dfrac{1}{3}[(b)^3 – (a)^3]\\&=\dfrac{b^3}{3}- \dfrac{a^3}{3} \end{aligned}
This show that $\int_{a}^{b} x^2\phantom{x}dx =\dfrac{b^3}{3}- \dfrac{a^3}{3} $.
Example 4
Evaluate the following definite integrals.
a. $ \int_{0}^{\pi} 3\sin \theta – 4\cos \theta\phantom{x}d\theta$
b. $\int_{0}^{1} 3x + 6\sqrt[3]{x^5}\phantom{x}dx$
c. $\int_{0}^{4} |2x – 4|\phantom{x}dx$
Solution
Apply the second part of the fundamental theorem of calculus once more to evaluate the three definite integrals.
\begin{aligned}\int_{a}^{b}f(x)\phantom{x}dx &= F(b) – F(a)\\&= F(x)|_{a}^{b}\end{aligned}
Find the exact value of $ \int_{0}^{\pi} 3\sin \theta – 4\cos \theta\phantom{x}d\theta$ by finding the antiderivative of $\int 3\sin \theta – 4\cos \theta\phantom{x}d\theta$.
\begin{aligned}\int 3\sin \theta -4\cos \theta\phantom{x}d\theta &= 3\int\sin \theta\phantom{x}d\theta -4\int\cos \theta\phantom{x}d\theta,\phantom{x}\color{Teal}\text{Difference Rule}\\&= 3({\color{Teal}-\cos \theta +C}) – 4({\color{Orchid}\sin \theta +C}),\phantom{x}{\color{Teal}\text{Integral of sin}}\text{ & }{\color{Orchid}\text{Integral of cos}}\\&= -3\cos \theta – 4\sin \theta + C\end{aligned}
Now that we have $F(\theta) = -3\cos \theta – 4\sin \theta$ as the antiderivative of the expression, find the difference of $F(\pi)$ and $F(0)$.
\begin{aligned}\int_{0}^{\pi} 3\sin \theta -4\cos \theta\phantom{x}d\theta &= -3\cos \theta – 4\sin \theta |_{0}^{\pi}\\&= [(-3\cos\pi – 4\sin\pi) – (-3\cos0 – 4\sin0)]\\&= [-3(-1) – 4(0) + 3(1) + 4(0)]\\&= 6 \end{aligned}
Hence, we’ve shown you that $ \int_{0}^{\pi} 3\sin \theta – 4\cos \theta\phantom{x}d\theta = 6$.
For $\int_{0}^{1} 3x + 6\sqrt[3]{x^5}\phantom{x}dx$, rewrite the second term as a power of $x$ then work on finding its antiderivative.
\begin{aligned}\int 3x + 6\sqrt[3]{x^5}\phantom{x}dx&=\int 3x + 6x^{\frac{5}{3}}\phantom{x}dx\\ &= \int 3x\phantom{x}dx + \int 6x^{\frac{5}{3}}\phantom{x}dx,\phantom{x}\color{Teal}\text{Sum Rule}\\ &= 3\int x\phantom{x}dx + 6\int x^{\frac{5}{3}}\phantom{x}dx,\phantom{x}\color{Teal}\text{Constant Multiple Rule}\\&= 3\left({\color{Teal}\dfrac{x^{1 +1}}{1 + 1}} \right )+ 6\left({\color{Teal}\dfrac{x^{\frac{5}{3} +1}}{\frac{5}{3} + 1}} \right ) +C,\phantom{x}\color{Teal}\text{Power Rule}\\&= \dfrac{3}{2}x^2 + \dfrac{9}{4}x^{\frac{8}{3}} + C\end{aligned}
Evaluate the antiderivative at $x= 0$ and $x= 1$ then subtract the result to find the definite integral.
\begin{aligned}\int_{0}^{1} 3x + 6\sqrt[3]{x^5}\phantom{x}dx&= \dfrac{3}{2}x^2 + \dfrac{9}{4}x^{\frac{8}{3}}|_{0}^{1}\\&=\left[\left(\dfrac{3}{2}\cdot1^2 + \dfrac{9}{4}\cdot 1^{\frac{8}{3}}\right)-\left(3\cdot0^3 + \dfrac{9}{4}\cdot 0^{\frac{8}{3}}\right)\right]\\&=\dfrac{15}{4} \end{aligned}
This means that $\int_{0}^{1} 3x + 6\sqrt[3]{x^5}\phantom{x}dx = \dfrac{15}{4} $.
Before we evaluate the definite integral, $\int_{0}^{4} |2x – 4|\phantom{x}dx$, let’s first observe the behavior of $2x – 4$ at these two intervals: $x < 2$ and $x > 2$.
- When $x < 2$, $2x – 4$ is negative.
- When $x > 2$, $2x – 4$ is positive.
Since the signs change depending on $x$’s values, let’s divide the definite integral into two parts using the sum property of definite integrals:
\begin{aligned}\int_{0}^{4} |2x -4|\phantom{x}dx &= \int_{0}^{2} |2x – 4|\phantom{x}dx + \int_{2}^{4} |2x – 4|\phantom{x}dx \end{aligned}
Drop the absolute values to simplify these two expressions. Account for the negative sign for the first part.
\begin{aligned}\int_{0}^{2} |2x – 4|\phantom{x}dx + \int_{2}^{4} |2x – 4|\phantom{x}dx &=\int_{0}^{2} -(2x – 4)\phantom{x}dx + \int_{2}^{4} 2x – 4\phantom{x}dx \end{aligned}
Find the antiderivative for each group of expressions as shown below.
| \begin{aligned}\boldsymbol{\int-(2x – 4)\phantom{x}dx}\end{aligned} | \begin{aligned}\int -(2x – 4)\phantom{x}dx &= \int-2(x -2)\phantom{x}dx\\&=-2\int (x -2)\phantom{x}dx,\phantom{x}\color{Teal}\text{Constant Multiple Rule}\\&=-2\left({\color{Teal}\int x \phantom{x}dx-\int 2\phantom{x}dx }\right ),\phantom{x}\color{Teal}\text{Sum Rule}\\&=-2\left({{\color{Teal}\dfrac{x^{1+1}}{1 + 1}}- {\color{Orchid}2x} }\right )+C,\phantom{x}{\color{Teal}\text{Power Rule}}\text{ & }{\color{Orchid}\text{Constant Rule}}\\&=-x^2 +4x\end{aligned} |
| \begin{aligned}\boldsymbol{\int (2x -4)\phantom{x}dx}\end{aligned} | \begin{aligned}\int (2x – 4)\phantom{x}dx &= \int2(x -2)\phantom{x}dx\\&=2\int (x -2)\phantom{x}dx,\phantom{x}\color{Teal}\text{Constant Multiple Rule}\\&=2\left({\color{Teal}\int x \phantom{x}dx-\int 2\phantom{x}dx }\right ),\phantom{x}\color{Teal}\text{Sum Rule}\\&=2\left({{\color{Teal}\dfrac{x^{1+1}}{1 + 1}}- {\color{Orchid}2x} }\right )+C,\phantom{x}{\color{Teal}\text{Power Rule}}\text{ & }{\color{Orchid}\text{Constant Rule}}\\&=x^2 -4x\end{aligned} |
Use these antiderivatives then evaluate the expression at the given upper and lower limits.
\begin{aligned}\int_{0}^{2} -(2x- 4)\phantom{x}dx + \int_{2}^{4} 2x – 4\phantom{x}dx&= (-x^2 +4x)|_{0}^{2} + (x^2 -4x)|_{2}^{4} \\&= [(-2^2 + 4\cdot 2)-(-0^2 + 4\cdot 0)]\\&+ [(4^2 – 4\cdot 4)-(2^2 – 4\cdot 2)]\\&=4 + 4\\&= 8\end{aligned}
Hence, we have $\int_{0}^{4} |2x – 4|\phantom{x}dx = 8$. This problem shows us how it’s possible to evaluate the definite integrals of absolute value functions.
Example 5
Find the area of the region bounded by the graphs of the following:
- The curve of $y = \dfrac{1}{2}x^2 – 2x$.
- The $x$-axis.
- The vertical lines: $x = 5$ and $x 10$.
Solution
Graph these lines and observe the bounded region they form.
- Draw the parabola with a vertex of $(2, -2)$.
- Draw two dashed vertical lines representing $x =5$ and $x =10$.
- The region is bounded at the $x$-axis too, so account for that when shading the region.
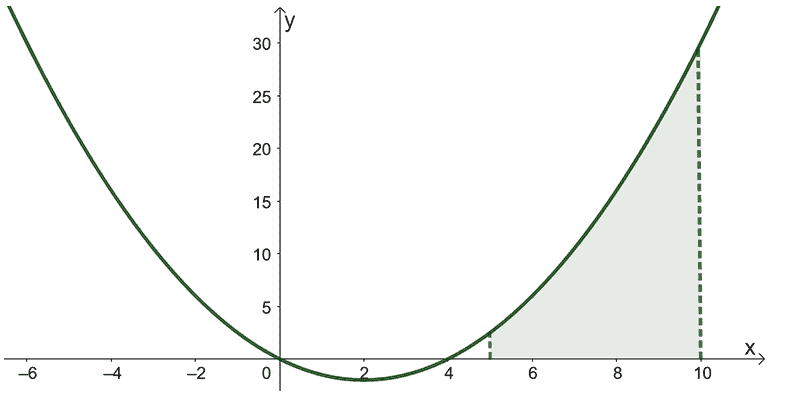
The area shown by the graph above can be represented by definite integral of the curve, $y = \dfrac{1}{2}x^2 – 2x$. Since the area is bounded from $x = 5$ and $x = 10$, we can use these as the definite integral’s lower and upper limits, respectively.
\begin{aligned}\text{Area} &= \int_{5}^{10} \left(\dfrac{1}{2}x^2-2x \right)\phantom{x}dx\end{aligned}
To find the area of the shaded region, we can evaluate the definite integral, $\int_{5}^{10} \left(\dfrac{1}{2}x^2-2x \right)\phantom{x}dx$ instead. Begin by finding the antiderivative’s expression.
\begin{aligned}\int\left(\dfrac{1}{2}x^2-2x \right)\phantom{x}dx &= \int\dfrac{1}{2}x^2 dx- \int 2x \phantom{x}dx,\phantom{x}\color{Teal}\text{Difference Rule}\\&= {\color{Teal}\dfrac{1}{2}\int x^2 dx}- {\color{Teal}2\int x \phantom{x}dx},\phantom{x}\color{Teal}\text{Constant Multiple Rule}\\&= \dfrac{1}{2}\left({\color{Teal}\dfrac{x^{2 + 1}}{2 + 1}} \right ) – 2\left({\color{Teal}\dfrac{x^{1 + 1}}{1 + 1}}\right) + C,\phantom{x}\color{Teal}\text{Power Rule}\\&= \dfrac{1}{6}x^3 – x^2 +C\end{aligned}
Find the definite integral by evaluating $\dfrac{1}{6}x^3 – x^2 |_{5}^{10}$.
\begin{aligned}\int_{5}^{10}\left(\dfrac{1}{2}x^2-2x \right)\phantom{x}dx &= \dfrac{1}{6}x^3 – x^2|_{5}^{10} \\&= \left[\left(\dfrac{1}{6}\cdot 10^3 – 10^2 \right )-\left(\dfrac{1}{6}\cdot 5^3 – 5^2 \right ) \right ]\\&= \dfrac{1000}{6} -100 – \dfrac{125}{6}+ 25\\&= \dfrac{425}{6}\\&\approx 70.83\end{aligned}
This means that the area of the region is equal to $\dfrac{425}{6}$ squared units or approximately $70.83$ squared units.
Example 6
Using the second part of the fundamental theorem of calculus, show that a circle with a radius of $2$ and centered at the origin has an area of $4\pi$ squared units.
Here’s a tip: $\int \sqrt{4-x^2}\phantom{x}dx =\frac{1}{2}\sqrt{4 – x^2} + 2\sin^{-1}\left(\dfrac{x}{2}\right) + C$
Solution
Graph the circle that’s being described – centered at the origin, $(0, 0)$, and has a radius of $2$ units. Here’s the graph of the circle we want to work with and we’ve highlighted a quarter of the circle.
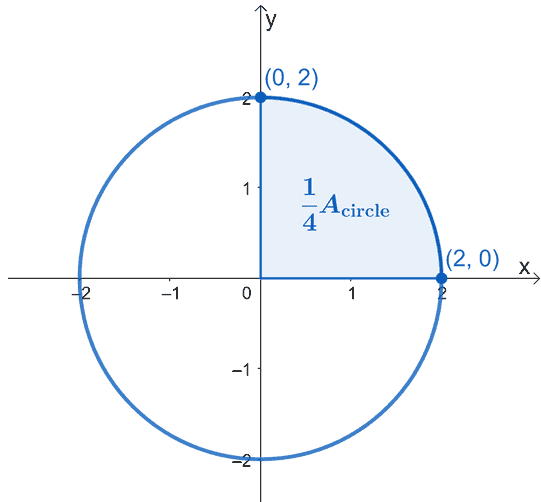
The area of the circle, $A_{\text{circle}}$ simply equal to four times the area of the shaded sector. This means that we can work on one quarter first then just multiply the resulting area by $4$.
Using the fundamental theorem of calculus, what we can do is evaluate the definite integral of the curve from $x =0$ to $x =2$. The equation of the circle we’re working with is $x^2 + y^2 = 4$, so isolate $y$ on the left-hand side first to rewrite the expression as a function of $x$.
\begin{aligned}x^2 + y^2 &= 4\\y^2 &= 4 – x^2 \\y&= \pm \sqrt{4 – x^2}\end{aligned}
Since we’re working with the upper sector, we’ll disregard the negative root. Hence, we have the definite integral, $\int_{0}^{2} \sqrt{4 – x^2}\phantom{x}dx$. This represents one-fourth of the circle, so we’ll have to multiply the resulting by $4$ to find the circle’s area.
\begin{aligned}A_{\text{circle}} &= 4\int_{0}^{2} \sqrt{4 – x^2}\phantom{x}dx \end{aligned}
Let’s use the hint: $\int \sqrt{4-x^2}\phantom{x}dx =\frac{1}{2}x\sqrt{4 – x^2} + 2\sin^{-1}\left(\dfrac{x}{2}\right) + C$ to evaluate the definite integral. Don’t worry; you’ll eventually learn how to integrate expressions like this through trigonometric substitution.
\begin{aligned}A_{\text{circle}} &= 4\left[\dfrac{1}{2}x\sqrt{4 -x^2} + 2\sin^{-1}\left(\dfrac{x}{2}\right) \right]_{0}^{2}\\&= 4\left[\dfrac{1}{2}(2)\sqrt{4 – 2^2} + 2\sin^{-1}\left(\dfrac{2}{2} \right )-\dfrac{1}{2}(0)\sqrt{4 – 0^2} – 2\sin^{-1}\left(\dfrac{0}{2} \right ) \right ]\\&= 4(0 +\pi – 0 -0)\\&= 4\pi \end{aligned}
This means that the area of four quadrants or the complete circle is $4\pi$ squared units. Hence, through the second part of the fundamental theorem of calculus, we were able to show that the area of a circle with a radius of $2$ units is $4\pi$ squared units.
Example 7
In Physics, the displacement of an object represents the object’s position from the time, $t = a$ and $t = b$. Let’s say the object’s position is $f(t)$ and velocity is $v(t)$, we have the following equations for its displacement:
\begin{aligned}\text{displacement} &= f(b) – f(a)\\&= \int_{a}^{b} v(t)\phantom{x}dt\end{aligned}
Jaimie’s car is traveling in a straight line with velocity at time $t$ seconds
given by $v(t) = \dfrac{8 – t}{2} \text{ m/s}$. What is the car’s displacement from time $t = 0$ to $t = 12$?
Solution
Since the function for velocity is given, use it to find the car’s displacement from $t =0$ to $t =12$. Use our definition for definite integral to evaluate $\int_{0}^{12} \dfrac{8 – t}{2}\phantom{x}dt$.
\begin{aligned}\text{displacement}&= \int_{0}^{12} \dfrac{8 – t}{2}\phantom{x}dt\\&=\dfrac{1}{2}\int_{0}^{12}
(8 -t)\phantom{x}dt,\phantom{x}\color{Teal}\text{Constant Multiple Rule}\\&= \dfrac{1}{2}\left[ \int_{0}^{12}
8\phantom{x}dt – \int_{0}^{12} t\phantom{x}dt\right ],\phantom{x}\color{Teal}\text{Difference Rule}\\&= \dfrac{1}{2}\left[\left({\color{Teal}8t} \right )|_{0}^{12} -{\color{Orchid} \dfrac{1}{2}t^2}|_{0}^{12} \right ],\phantom{x}{\color{Teal}\text{Constant Rule}}\text{ & }{\color{Orchid}\text{Power Rule}}\\&= \dfrac{1}{2}\left[(8 \cdot 12) – (8 \cdot 0) – \dfrac{1}{2}(12^2 -0^2)\right]\\&= 12\end{aligned}
This means that the car’s displacement is $12$ meters.
Use the relationship of displacement and velocity shown to answer the problem below.
Example 8
Alvin and Kevin are racing on their bicycles. They race along a long, straight track, and they agreed that whoever has gone the farthest after $8$ seconds gets a prize. These are the information we know about their cycling speeds:
- Alvin can cycle at a velocity of $v_1(t)=6 + 1.5t$ ft/sec.
- Kevin can cycle at a velocity of $v_2(t)=12+ \cos(\pi/2 t)$ ft/sec.
Using these two functions, who is going to win the race?
Solution
Recall that the displacement can be determined by evaluating the definite integral, $\int_{a}^{b} v(t)\phantom{x}dt$, where $v(t)$ represents the velocity.
Let’s find the displacements reached by Alvin and Keven from $t= 0$ and $t = 8$ seconds.
| Alvin’s Displacement | \begin{aligned}\text{displacement}&= \int_{0}^{8} v_1(t)\phantom{x}dt\\&= \int_{0}^{8} (6 + 1.5t)\phantom{x}dt\\&=\left(\int_{0}^{8} 6\phantom{x}dt \right ) + \left(\int_{0}^{8} 1.5\phantom{x}dt \right ),\phantom{x}{\color{Teal}\text{Sum Rule}}\\&= \left[{\color{Teal}6t} \right ]_{0}^{8} + \left[{\color{Orchid}\dfrac{1.5}{2}t^2} \right ]_{0}^{8},\phantom{x}{\color{Teal}\text{Constant Rule}}\text{ & }{\color{Orchid}\text{Power Rule}}\\&= [6(8) – 6(0)] + \left[\dfrac{3}{4}(8)^2 -\dfrac{3}{4}(0)^2 \right ]\\&= 48 +48\\&= 96\end{aligned} |
| Kevin’s Displacement | \begin{aligned}\text{displacement}&= \int_{0}^{8} v_2(t)\phantom{x}dt\\&= \int_{0}^{8} [12+ \cos\left(\dfrac{\pi}{2} t\right)]\phantom{x}dt\\&=\left(\int_{0}^{8} 12\phantom{x}dt \right ) + \left[\int_{0}^{8} \cos\left(\dfrac{\pi}{2} t\right)\phantom{x}dt \right ],\phantom{x}{\color{Teal}\text{Sum Rule}}\\&= \left[{\color{Teal}12t} \right ]_{0}^{8} + \left[{\color{Orchid}\dfrac{2}{\pi}\sin\left(\dfrac{\pi}{2} t\right)} \right ]_{0}^{8},\phantom{x}{\color{Teal}\text{Constant Rule}}\text{ & }{\color{Orchid}\text{Integral of cos}}\\&= [12(8) – 12(0)] + \left[\dfrac{2}{\pi}\sin\dfrac{\pi}{4} -\dfrac{2}{\pi}\sin0 \right ]\\&= 96 +\dfrac{\sqrt{2}}{\pi}\\&= 96.45\end{aligned} |
We’d like to highlight this part in evaluating Kevin’s displacement: $\int \cos\left(\dfrac{\pi}{2}t\right)\phantom{x} dt$. We know that the antiderivative of $\cos x$ is $\sin x$ but we’ll have to account for the chain rule and hence, the constant $\dfrac{2}{\pi}$ before the antiderivative.
From the two displacements, we can see that Kevin reached further than Alvin by $\dfrac{\sqrt{2}}{\pi}$ or approximately $0.45$ units. This means that Kevin wins the race if we base it from $t= 0$ and $t = 8$ seconds.
Practice Questions
1. Differentiate the following expressions.
a. $f(x)= \int_{4}^{x} e^{t^2}\phantom{x} dt$
b. $g(x)= \int_{-8}^{x} \sqrt[3]{6 – 5t^2}\phantom{x} dt$
c. $h(x)= \int_{1}^{x^5} \sin t dt$
2. Differentiate the following expressions.
a. $f(x)= \int_{3}^{x^5} e^{2t}\phantom{x} dt$
b. $g(x)= \int_{x^2}^{1} \dfrac{t^4 + 1}{t^2 + 2}\phantom{x} dt$
c. $h(x)= \int_{1}^{\sqrt{x} \tan x} t^2\phantom{x} dt$
3. Evaluate the following definite integrals.
a. $ \int_{-10}^{10} 2x^4\phantom{x}dx$
b. $\int_{0}^{4} (-3x^2 + 4)\phantom{x}dx$
c. $\int_{a}^{b} x^3\phantom{x}dx$, where $a$ and $b$ are constants
4. Evaluate the following definite integrals.
a. $ \int_{0}^{3\pi} 2\cos \theta – \sin \theta\phantom{x}d\theta$
b. $\int_{0}^{1} 2x – 8\sqrt[4]{x^3}\phantom{x}dx$
c. $\int_{0}^{2} |2x – 5|\phantom{x}dx$
5. Find the area of the region bounded by the graphs of the following:
• The curve of $y = \dfrac{1}{3}x^3 – 3x$.
• The $x$-axis.
• The vertical lines: $x = 2$ and $x = 6$.
6. Find the area of the region bounded by the graphs of the following:
• The curve of $y = 4\cos x$.
• The $x$-axis.
• The vertical lines: $x = 0$ and $x = \dfrac{\pi}{2}$.
7. Using the second part of the fundamental theorem of calculus, show that a circle with a radius of $3$ and centered at the origin has an area of $9\pi$ squared units.
Here’s a tip: $\int \sqrt{9-x^2}\phantom{x}dx =\frac{1}{2}x\sqrt{9 – x^2} + 9\sin^{-1}\left(\dfrac{x}{3}\right) + C$
8. Let’s say that $f(12) = 6$ and $f(x)$ is continuous. What is the value of $f(3)$ if $\int_{3}^{12}f^{\prime}(x)\phantom{x}dx =18$?
9. Jaimie’s car is traveling in a straight line with velocity at time $t$ seconds
given by $v(t) = \dfrac{12 – t}{2} \text{ m/s}$. What is the car’s displacement from time $t = 0$ to $t = 16$?
10. Sarah and Marie are racing on their bicycles. They race along a long, straight track, and they agreed that whoever has gone the farthest after $12$ seconds gets a prize. These are the information we know about their cycling speeds:
• Sarah can cycle at a velocity of $v_1(t)=8 + 2t$ ft/sec.
• Marie can cycle at a velocity of $v_2(t)=16 + \sin(\pi/2 t)$ ft/sec.
Using these two functions, who is going to win the race and by how many feet?
Answer Key
1.
a. $f^{\prime}(x) = e^{x^2}$
b. $g^{\prime}(x) = \sqrt[3]{6 – 5x^2}$
c. $h^{\prime}(x) = -5x^6 \sin(x^5)$
2.
a. $f^{\prime}(x) = 5e^{2x^5}x^4$
b. $g^{\prime}(x) = -\dfrac{2x\left(x^8+1\right)}{x^4+2} $
c. $h^{\prime}(x) = \dfrac{\sqrt{x}\tan ^2\left(x\right)\left(2x\sec ^2\left(x\right)+\tan \left(x\right)\right)}{2} $
3.
a. $\int_{-10}^{10} 2x^4\phantom{x}dx =80000$
b. $\int_{-10}^{10} 2x^4\phantom{x}dx =-48$
c.$ \int_{a}^{b} x^3\phantom{x}dx = \dfrac{b^4}{4} – \dfrac{a^4}{4}$
4.
a. $\int_{0}^{3\pi} 2\cos \theta – \sin \theta\phantom{x}d\theta =-2$
b. $\int_{0}^{1} 2x – 8\sqrt[4]{x^3}\phantom{x}dx = -\dfrac{25}{7}$
c. $\int_{0}^{2} |2x – 5|\phantom{x}dx =6$
5. Area is equal to $\dfrac{176}{3}$ squared units or approximately $58.67$ squared units.
6. Area is equal to $4$ squared units.
7.
Equation of circle centered at the origin and has a radius of $3$ units:
$\begin{aligned}x^2 + y^2 &= 9\\y^2 &= 9 – x^2 \\y&= \sqrt{9 – x^2}\end{aligned}$
Evaluate the definite integral shown below to find the circle’s area:
$\begin{aligned}A_{\text{circle}} &=4\int_{0}^{3} \sqrt{9 – x^2}\phantom{x}dx\\ &=4\left[\dfrac{1}{2}x\sqrt{9 -x^2} + \dfrac{9}{2}\sin^{-1}\left(\dfrac{x}{3}\right) \right]_{0}^{3}\\&= 4\left[\dfrac{1}{2}(3)\sqrt{9 – 3^2} + \dfrac{9}{2}\sin^{-1}\left(\dfrac{3}{3} \right )-\dfrac{1}{2}(0)\sqrt{9 – 0^2} – \dfrac{9}{2}\sin^{-1}\left(\dfrac{0}{3} \right ) \right ]\\&= 4\left(0 +\dfrac{9}{2}\cdot\dfrac{\pi}{2} – 0 -0\right)\\&= 9\pi \end{aligned}$
8.
$\begin{aligned}\int_{3}^{12}f^{\prime}(x)\phantom{x}dx &= f(12) – f(3)\\\\18 &= 6 – f(3)\\f(3) &= -12\end{aligned}$
9. $32$ meters
10. Marie won the race by $48$ feet.
Images/mathematical drawings are created with GeoGebra.
