Golden Ratio – Explanation and Examples

The golden ratio is an intriguing mathematical relation between two quantities. Moreover, it is an interesting concept mathematically and from an aesthetic and sometimes metaphysical point of view.

Two quantities $a$ and $b$ with $a > b$ are said to be in golden ratio if $\dfrac{ a + b}{a} = \dfrac{a}{b}$

The ratio $\frac{a}{b}$ is also denoted by the Greek letter $\Phi$ and we can show that it is equal to $\frac{1 + \sqrt{5}}{2} \approx 1.618$. Note that the golden ratio is an irrational number, i.e., the numbers of the decimal point continue forever without any repeating pattern, and we use $1.618$ as an approximation only. Some other names for the golden ratio are golden mean, golden section, and divine proportion.

What is the golden ratio:

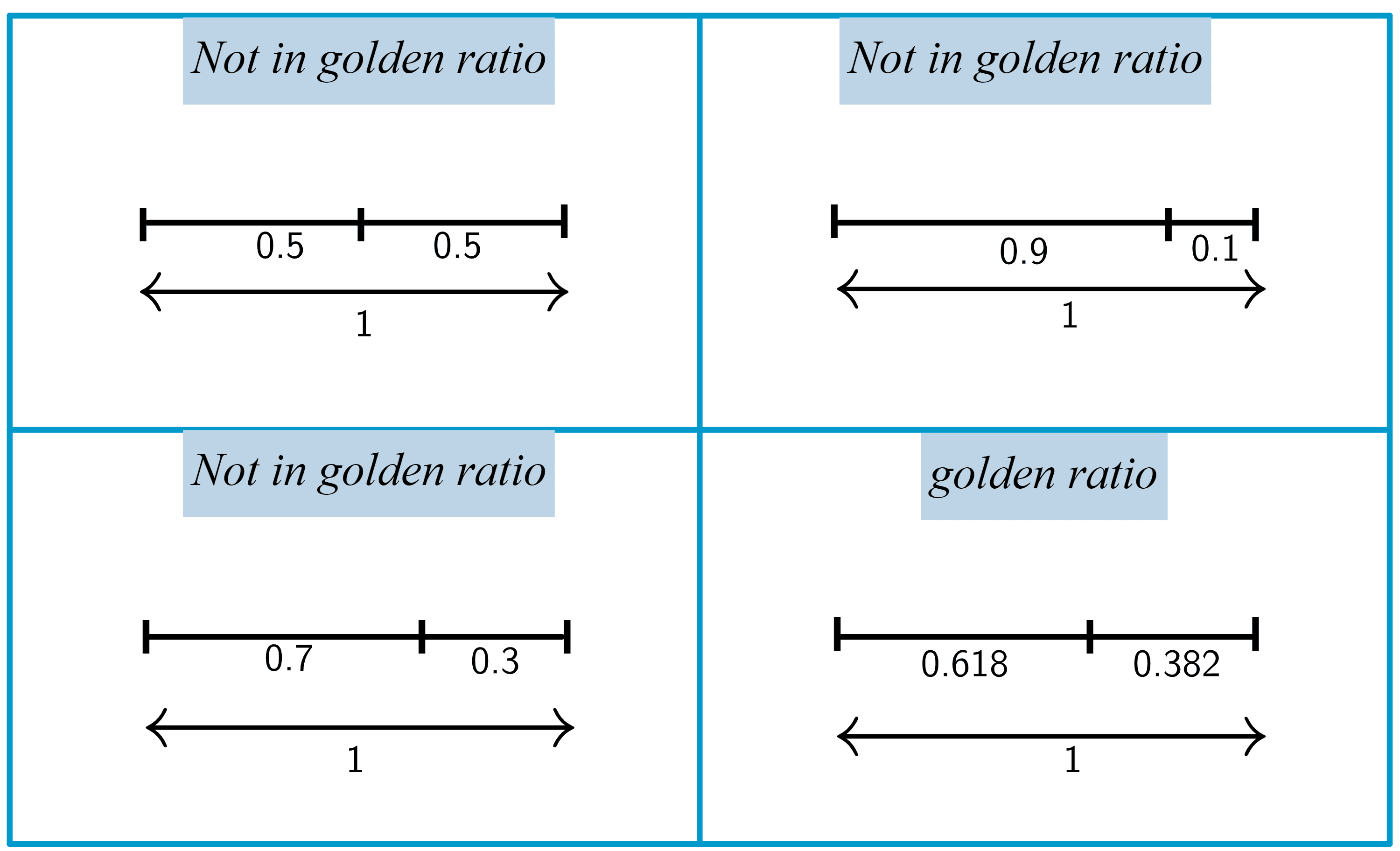
Golden ration can easily be understood using the example of a stick that we break into two unequal parts $a$ and $b$, where $a>b$, as shown in the figure below

Now there are many ways in which we can break the stick into two parts; however, if we break it in a particular manner, i.e., the ratio of the long part ($a$) and the short part ($b$) is also equal to the ratio of the total length ($a + b$) and the long part ($a$), then $a$ and $b$ are said to be in the golden ratio. The figure below shows an example of when the two parts of a stick are in the golden ratio and when they are not.

Calculating the golden ratio:

We stated above that the golden ratio is exactly equal to $\frac{1 + \sqrt{5}}{2}$. Where does this number come from? We will describe two methods to find the value $\Phi$. First, we start with the definition that $a$ and $b$ are in golden ratio if

$\frac{a}{b} = \frac{a + b}{a} = 1 + \frac{b}{a}$

Let $\Phi = \frac{a}{b}$ then $\frac{b}{a} = \frac{1}{\Phi}$, so the above equation becomes

$\Phi = 1 + \frac{1}{\Phi}$.

Method-1: The recursive method

We assume any value for the $\Phi$, lets say we assume $\Phi=1.2$. Now, we put this value in the above formula, i.e., $\Phi = 1 + \frac{1}{\Phi}$ and get a new value of $\Phi$ as follows:

$\Phi = 1 + \frac{1}{1.2} = 1.8333$.

Now, we put this new value again in the formula for the golden ratio to get another value, i.e.,

$\Phi = 1 + \frac{1}{1.8.3333} = 1.54545$.

If we keep on repeating this process, we get closer and closer to the actual value of $\Phi$. As we show in the table below

Method-2: The quadratic formula

Using the fact that $\Phi = 1 + \frac{1}{\Phi}$ and multiplying by $\Phi$ on both sides, we get a quadratic equation.

$\Phi^2 = \Phi + 1$.

This can also be rearranged as

$\Phi^2 – \Phi – 1 = 0$.

By using the quadratic formula for the equation $\alpha x^2 + \beta x + c = 0$, and noting that $x=\Phi$, $\alpha=1$, $\beta=-1$ and $c=-1$, we get

$\Phi = \frac{1 \pm \sqrt{1- 4 \times 1 \times -1}}{2} = \frac{1  \pm \sqrt{5}}{2}$.

The quadratic equation always has two solutions, in this case, one solution, i.e., $\frac{1  + \sqrt{5}}{2}$ is positive and the second solution, i.e., $\frac{1  – \sqrt{5}}{2}$ is negative. Since we assume $\Phi$ to be a ratio of two positive quantities, so the value of $\Phi$ is equal to $\frac{1  + \sqrt{5}}{2}$, which is approximately equal to 1.618.

Golden ratio definition:

Using the above discussion, we can define the golden ratio simply as:

The golden ratio $\Phi$ is the solution to the equation $\Phi^2 = 1  + \Phi$.

Golden ratio examples:

There are many interesting mathematical and natural phenomenon where we can observe the golden ratio. We describe some of these below

The golden ratio and the Fibonacci numbers

The Fibonacci numbers are a famous concept in number theory. The first Fibonacci number is 0, and the second is 1. After that, each new Fibonacci number is created by adding the previous two numbers. For example, we can write the third Fibonacci number by adding the first and the second Fibonacci number, i.e., 0 + 1 = 1. Likewise, we can write the fourth Fibonacci number by adding the second and third Fibonacci numbers, i.e., 1+1 = 2, etc. The sequence of Fibonacci numbers is called a Fibonacci sequence and is shown below:

$0, \,\, 1, \,\, 1, \,\, 2,\,\, 3,\,\, 5,\,\, 8,\,\, 13,\,\, 21,\,\, 34, \cdots$

If we start dividing subsequent Fibonacci numbers, the results approach closer and closer to the golden ratio as shown in the table below:

Golden ratio in Geometry

Pentagon and pentagram

The golden ratio makes numerous appearances in a regular pentagon and its associated pentagram. We draw a regular pentagon in the figure below.

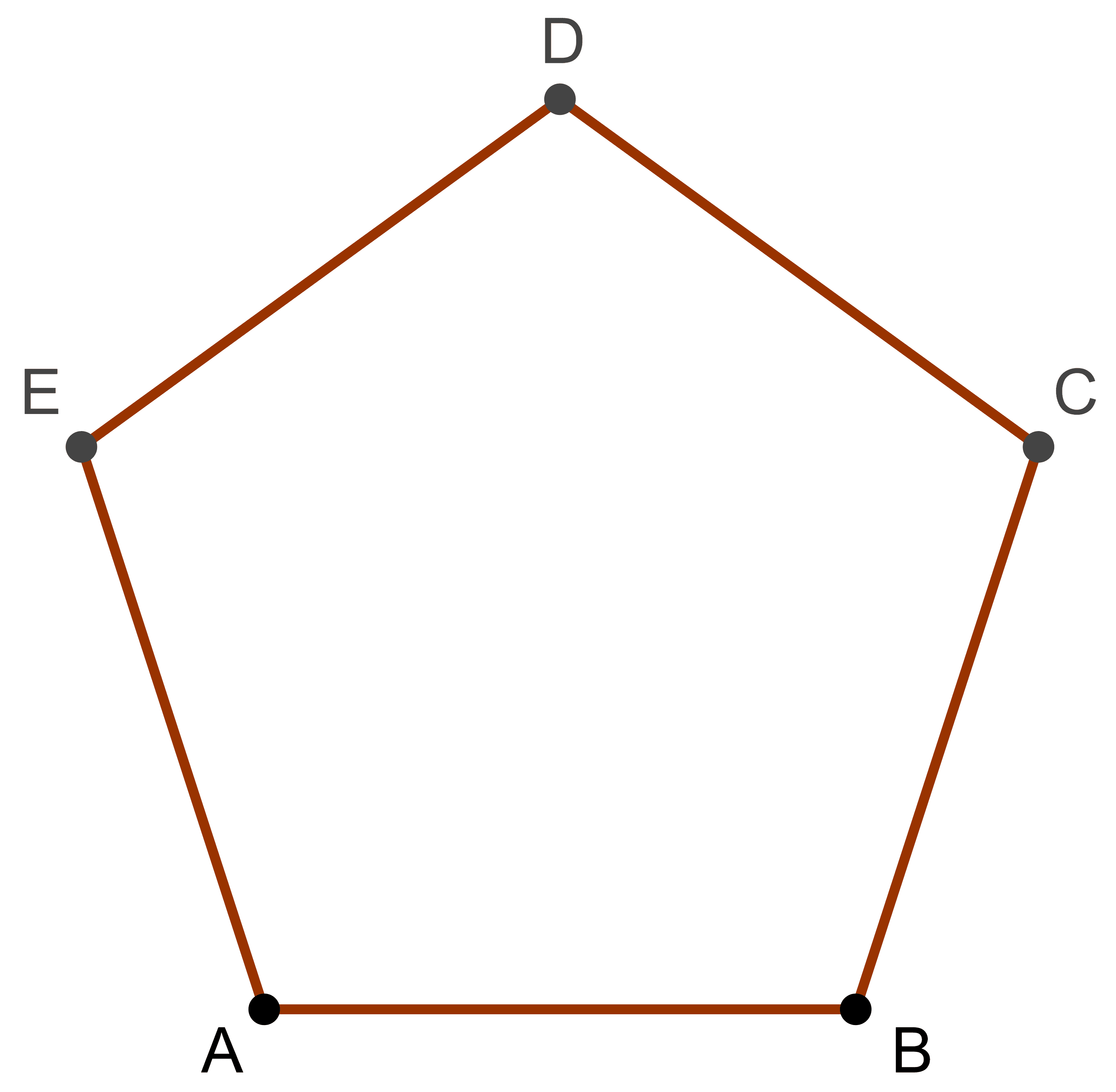
If we connect the vertices of the pentagon, we get a star-shaped geometrical figure inside, which is called a pentagram, shown below

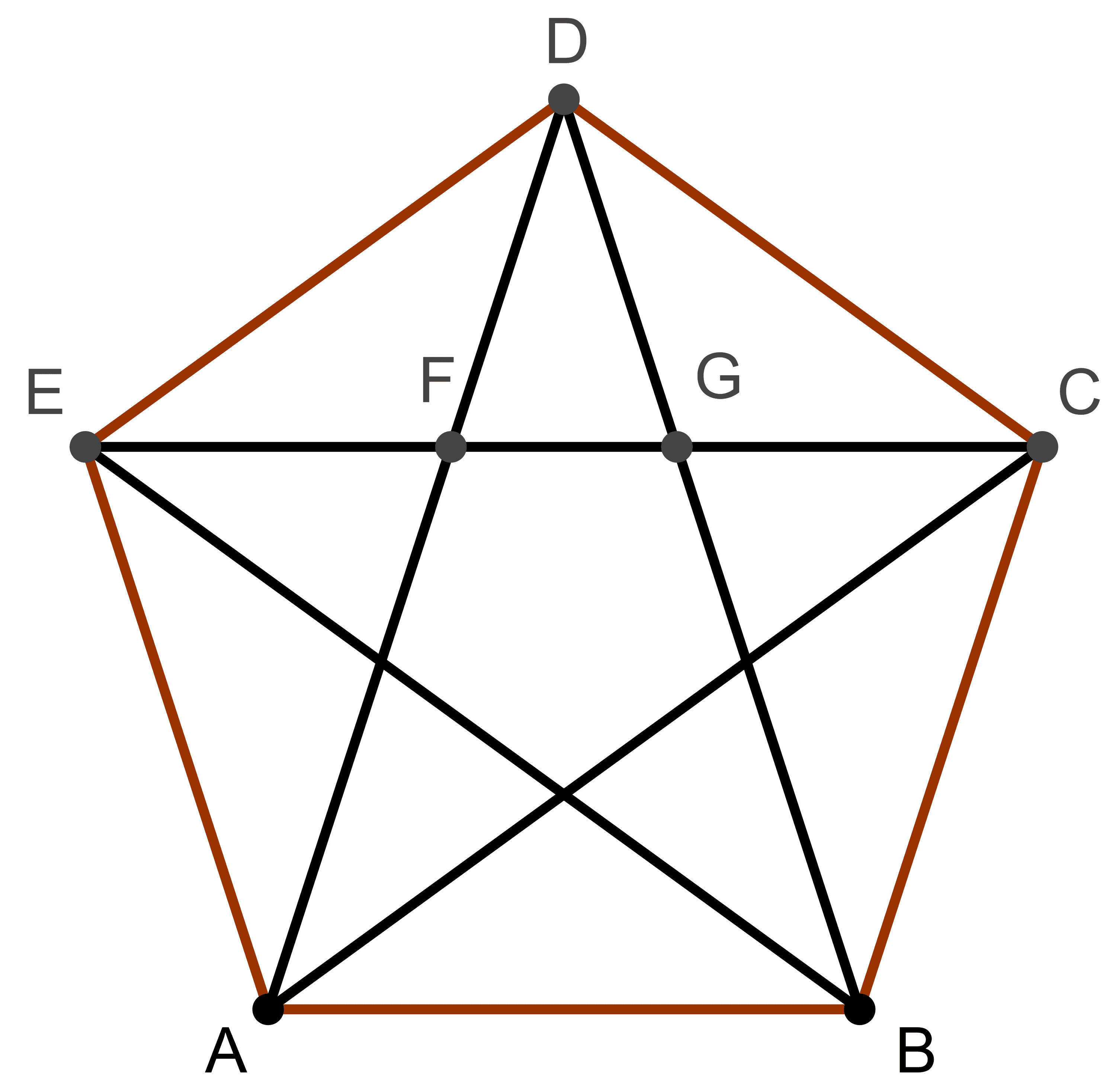
Many lines obey the golden ratio in the above figure. For example,

$\frac{DE}{EF}$ is in golden ratio

$\frac{EF}{FG}$ is in golden ratio

$\frac{EG}{EF}$ is in golden ratio

$\frac{BE}{AE}$ is in golden ratio,

$\frac{CF}{GF}$ is in golden ratio,

to name a few.

The golden spiral

Let us take a rectangle with one side equal to 1 and the other side equal to $\Phi$. The ratio of the large side to the small side is equal to $\frac{\Phi}{1}$. We show the rectangle in the figure below.

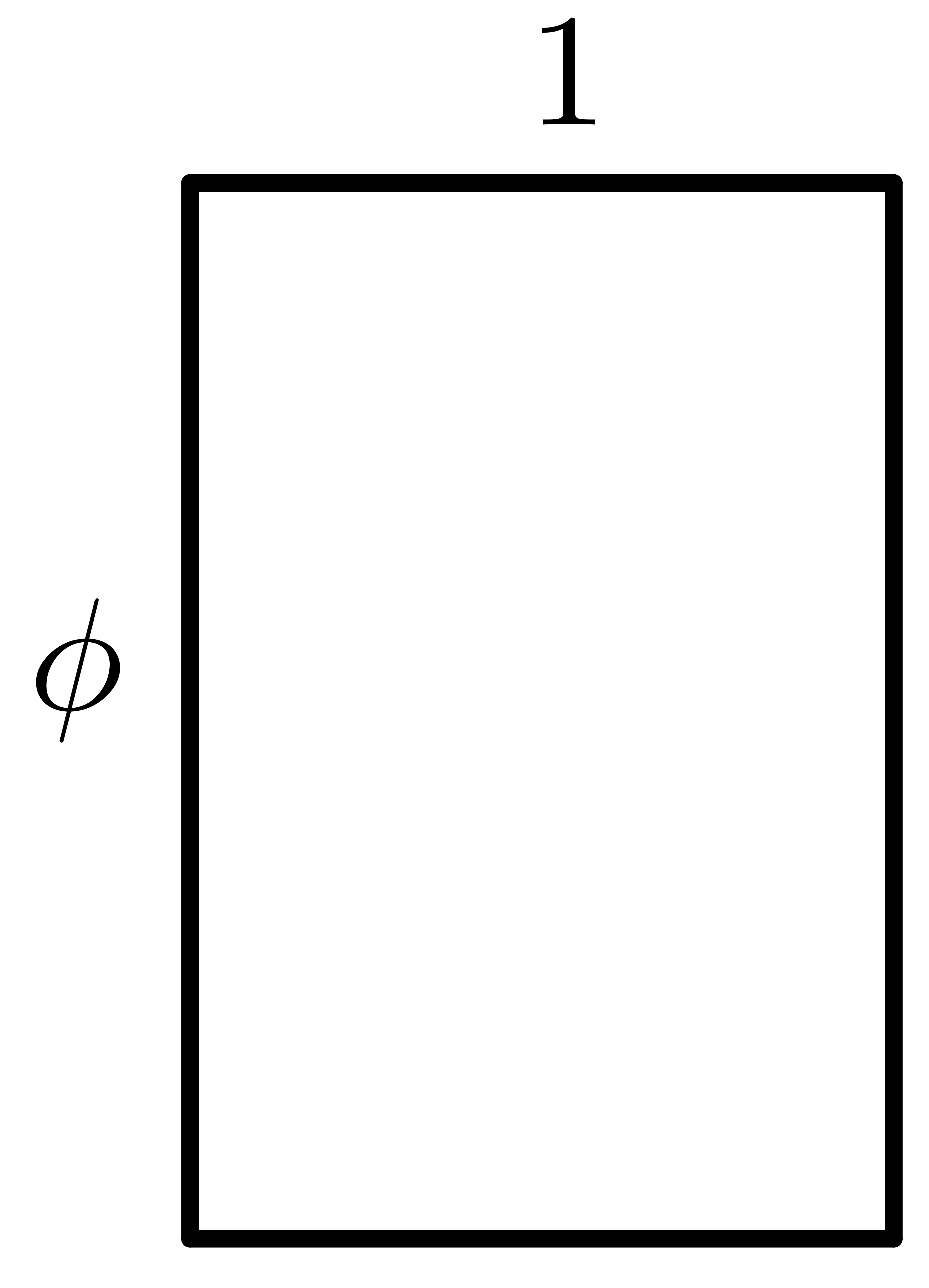
Now let’s say we divide the rectangle into a square of all sides equal to 1 and a smaller rectangle with one side equal to 1 and the other equal to $\Phi-1$. Now the ratio of the large side to the smaller one is $\frac{1}{\Phi-1}$. The new rectangle is drawn in blue in the figure below

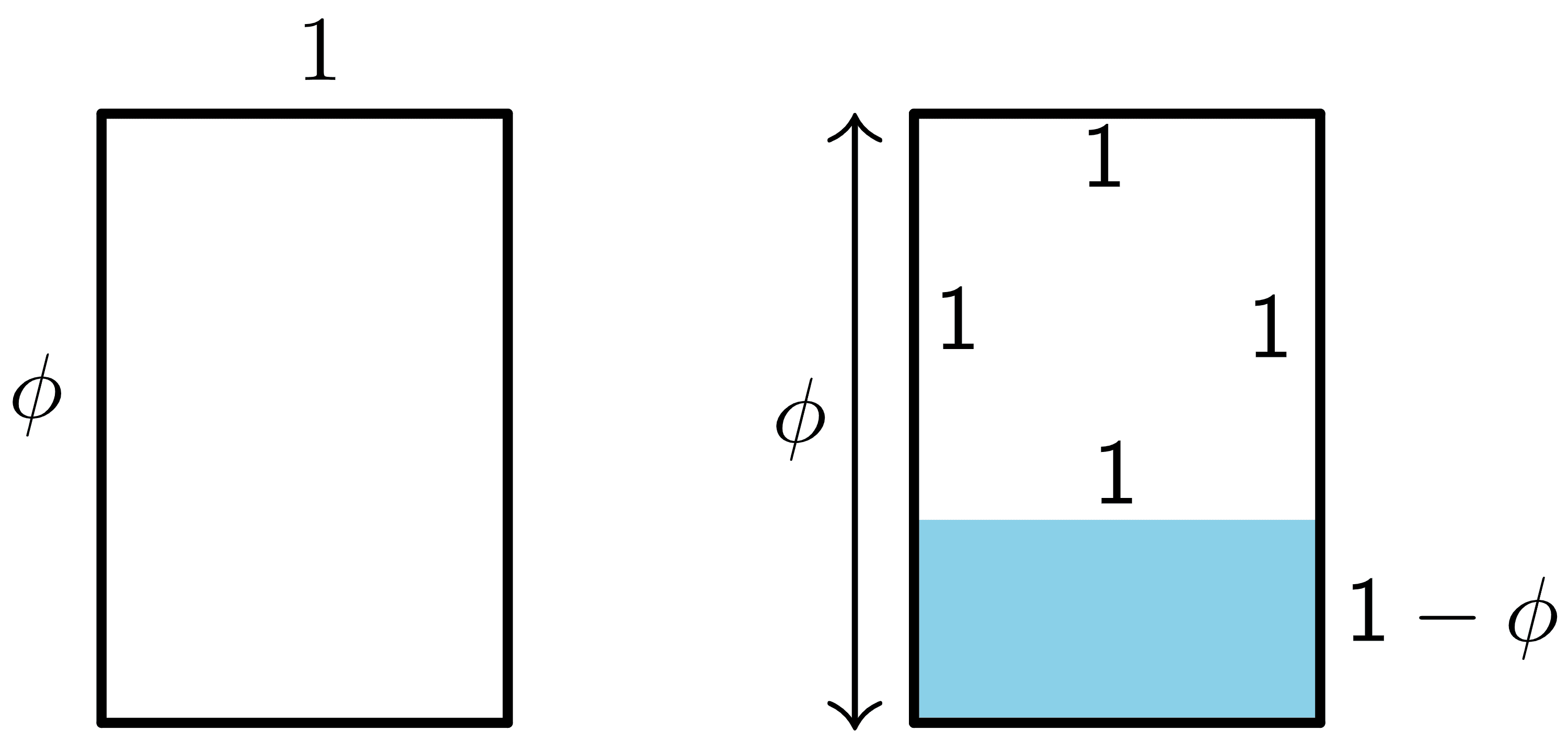
From the definition of the golden ratio, we note that

$\Phi^2 -\Phi -1 = 0$, we can rewrite it as

$\Phi(\Phi -1) = 1$, or

$\frac{\Phi}{1} = \frac{1}{\Phi -1}$

Hence, the new rectangle in blue has the same ratio of the large side to the small side as the original one. These rectangles are called golden rectangles. If we keep on repeating this process, we get smaller and smaller golden rectangles, as shown below.

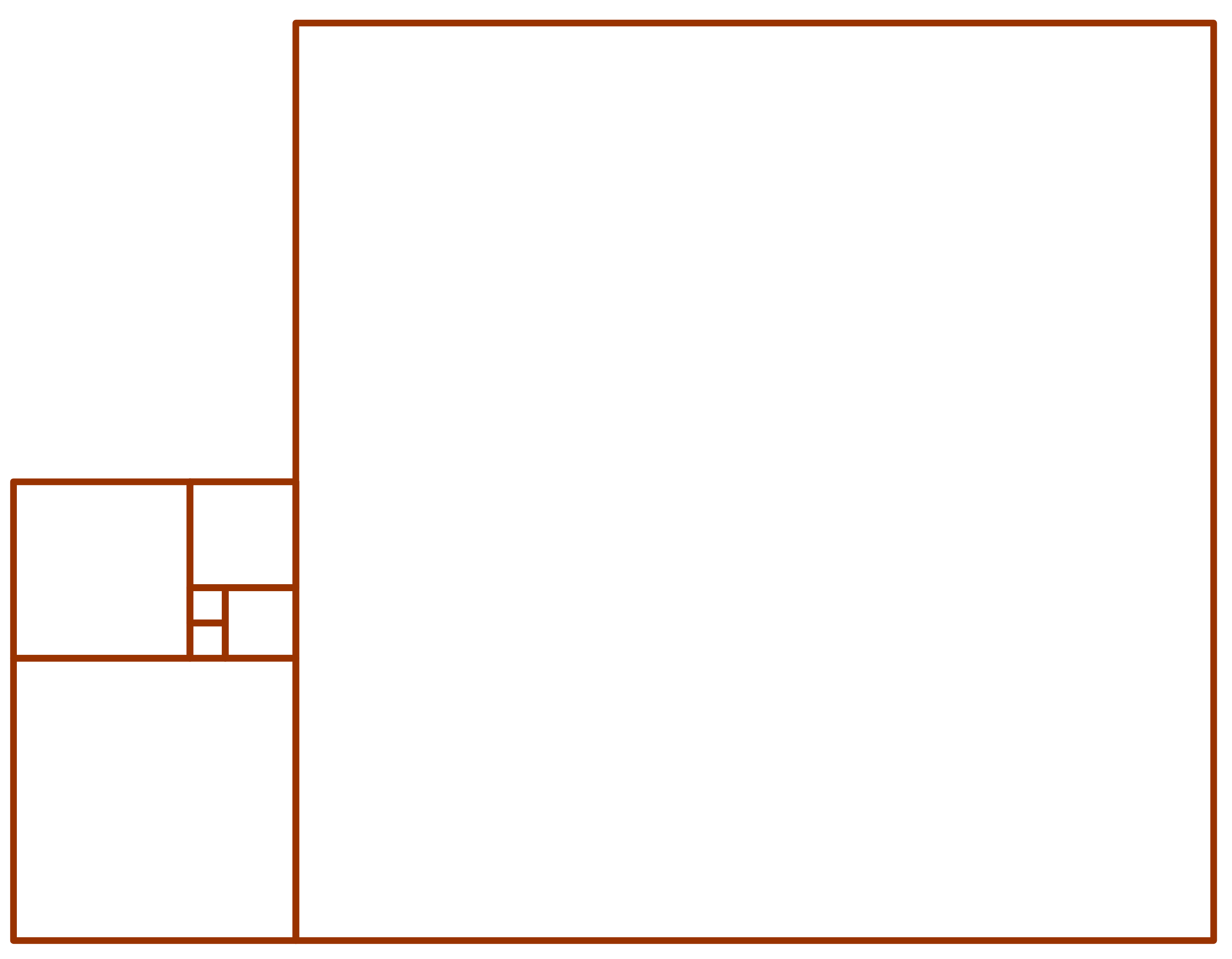
If we connect the points that divide the rectangles into squares, we get a spiral called the golden spiral, as shown below.

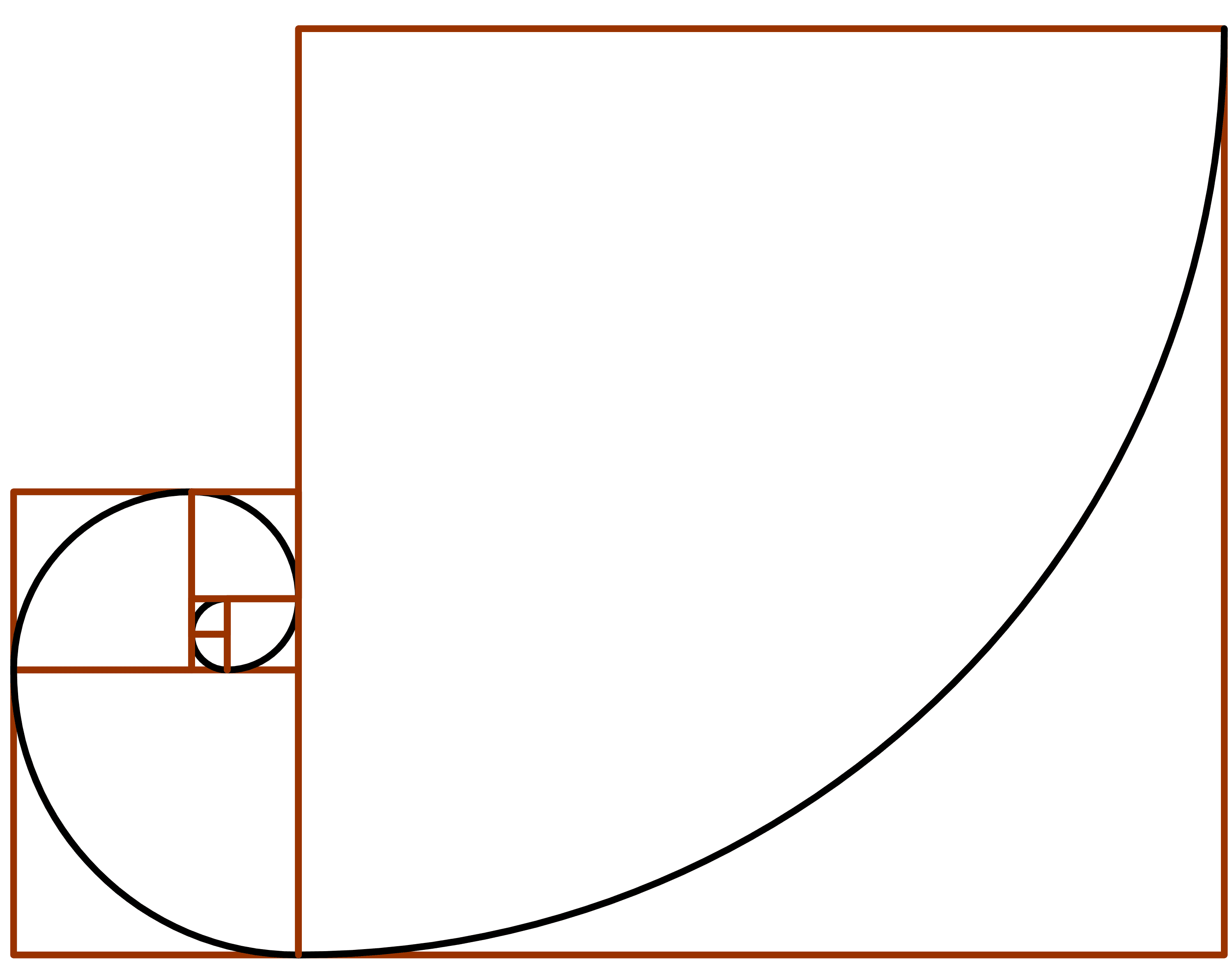
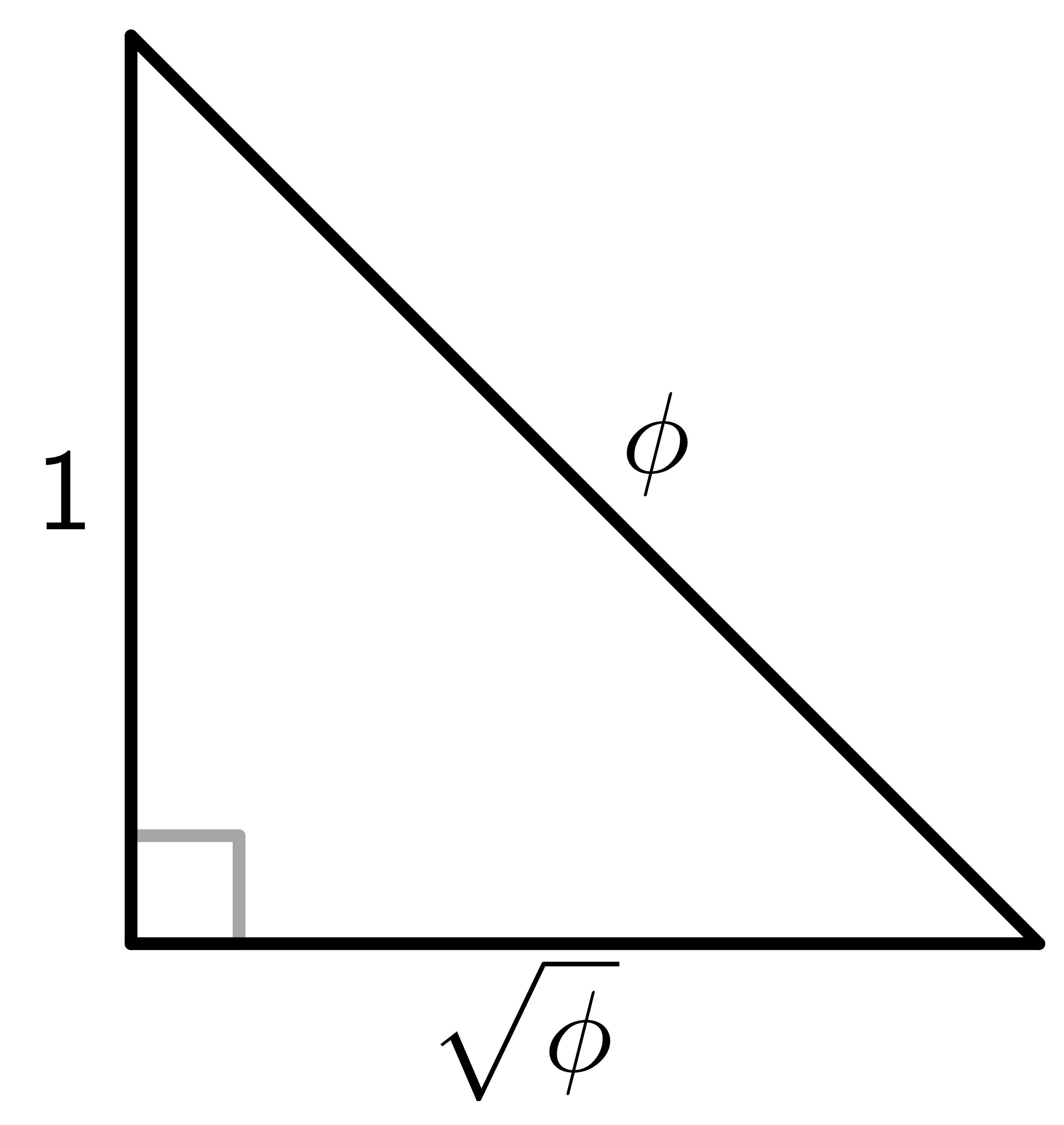
The Kepler triangle

The famous astronomer Johannes Kepler was fascinated by both the Pythagoras theorem and the golden ratio, so he decided to combine both in the form of Kepler’s triangle. Note that the equation for the golden ratio is

$\Phi^2 = \Phi + 1$.

It is similar in format to the Pythagoras formula for the right-angled triangle, i.e.,

$\textrm{Hypotenuse}^2 = \textrm{Base}^2 + \textrm{Perpendicular}^2$,

If we draw a right-angled triangle with hypotenuse equal to $\Phi$, base equal to $\sqrt{\Phi}$ and perpendicular equal to 1, it will be a right-angled triangle. Such a triangle is called the Kelper triangle, and we show it below:

Golden ratio in Nature

There are many natural phenomena where the golden ratio appears rather unexpectedly. Most readily observable is the spiraling structure and Fibonacci sequence found in various trees and flowers. For instance, in many cases, the leaves on the stem of a plant grow in a spiraling, helical pattern, and if we count the number of turns and number of leaves, we usually get a Fibonacci number. We can see this pattern in Elm, Cherry almond, etc. However, we must remember that many plants and flowers do not follow this pattern. Hence, any claim that the golden ratio is some fundamental building block of nature is not exactly valid.

It is also claimed that the ideal or perfect human face follows the golden ratio. But, again, this is highly subjective, and there is no uniform consensus on what constitutes an ideal human face. Also, all types of ratios can be found in any given human face.

In the human body, the ratio of the height of the naval to the total height is also close to the golden ratio. However, again we must remember that many ratios between 1 and 2 can be found in the human body, and if we enumerate them all, some are bound to be close to the golden ratio while others would be quite off.

Finally, the spiraling structure of the arms of the galaxy and the nautilus shell is also quoted as examples of the golden ratio in nature. These structures are indeed similar to the golden spiral mentioned above; however, they do not strictly follow the mathematics of the golden spiral.

How much of the golden ratio is actually present in nature and how much we force in on nature is subjective and controversial. We leave this matter to the personal preference of the reader.

Golden ration in architecture and design

Many people believe that the golden ratio is aesthetically pleasing, and artistic designs should follow the golden ratio. It is also argued that the golden ratio has appeared many times over the centuries in the design of famous buildings and art masterpieces.

For example, We can find the golden ratio many times in the famous Parthenon columns. Similarly, it is argued that the pyramids of Giza also contain the golden ratio as the basis of their design.

Some other examples are the Taj Mahal and Notre Damn etc. However, it should be remembered that We cannot achieve the perfect golden ratio as it is an irrational number. Since we are good at finding patterns, it may be the case that we are forcing the golden ratio on these architectures, and the original designers did not intend it.

However, some modern architectures, such as the United Nations secretariat buildings, have actually been designed using a system based on golden ratios.

Similarly, it is thought that Leonardo Di Vinci relied heavily on the use of the golden ratio in his works such as Mona Lisa and the Vitruvian Man. Whether the golden ratio is indeed aesthetic and it should be included in the design of architecture and art is a subjective matter and we leave this matter to the artistic sense of the reader.

If you are indeed interested in using the golden ratio in your works, some simple tips would be to use fonts, such as the heading font and the body text, such that they follow a golden ratio. Or divide your canvas or screen for any painting/pictures/documents so that the golden ratio is maintained.

Once you have used the golden ratio in your work, you will be in a better position to decide the aesthetic value of the golden ratio.

Golden ratio in History:

We have discussed the relation of the Fibonacci sequence and the golden ratio earlier. We can find the Fibonacci sequence in the works of Indian mathematicians as old as the second or third century BC. It was later taken up by Arab mathematicians such as Abu Kamil. From the Arabs, it was transmitted to Leonardo Fibonacci, whose famous book Liber abaci introduced it to the western world.

We have already mentioned some ancient structures such as the pyramids of Giza and the Parthenon that are believed to have applied the golden ratio in their designs. We also find mentions of the golden ratio in the works of Plato. Elements is an ancient and famous book on geometry by the Greek mathematician Euclid. We find some of the first mentions of the golden ratio as “extreme and mean ratio” in Elements.

The golden ratio gained more popularity during the Renaissance. Luca Pacioli, in the year 1509, published a book on the golden ratio called divine proportion. Leonardo Da Vinci did the illustrations of this book. Renaissance artists used the concept of the golden ratio in their works owing to its aesthetic appeal.

The famous astronomer Johannes Kepler also discusses the golden ratio in his writings, and we have also described the Kepler triangle above.

The term “Golden ratio” is believed to be coined by Martin Ohm in 1815 in his book “The Pure Elementary Mathematics.”

The Greek letter Phi (i.e., $\Phi$), which we have also used in this article to denote the golden ratio, was first used in 1914 by the American Mathematician Mark Barr. Note that Greek $\Phi$ is equivalent to the alphabet “F,” the first letter of Fibonacci.

More recently, Le Corbusier, the lead architect of the UN secretariat, created a design system based on the golden ratio of the UN secretariat building. In his bestseller book ” The Da Vinci Code, “the fiction writer Dan Brown popularized the myths and legends around the golden ratio in his bestseller book “The Da Vinci Code.”