Graphing Linear Inequalities – Explanation & Examples

Linear inequalities are numerical or algebraic expressions in which two values are compared by the use of inequality symbols such, < (less than), > (greater than), ≤ (less than or equal to), ≥ (greater than or equal to), and  ≠ (not equal to)

For example, 10 < 11, 20 > 17 are examples of numerical inequalities whereas, x > y, y < 19 – x, x ≥  z > 11 etc. are all the examples of algebraic inequalities. Algebraic inequalities are sometimes referred to as literal inequalities.

The inequality symbols ‘< ‘and ‘>’ are used to express the strict inequalities, whereas the symbols ‘≤’ and ‘≥’ represent slack inequalities.

How to Graph Linear Inequalities?

A linear inequality is the same as a linear equation, only that the inequality sign substitutes the equals sign. The same steps and concepts used to graph linear equations are also applied to graph linear inequalities.

The only difference between the two equations is that a linear equation gives a line graph. In contrast, a linear inequality shows the area of the coordinate plane that satisfies the inequality.

A linear inequality graph usually uses a borderline to divide the coordinate plane into two regions. One part of the region consists of all solutions to inequality. The borderline is drawn with a dashed line representing ‘>’ and ‘<‘ and a solid line representing ‘≥’ and ‘≤’.

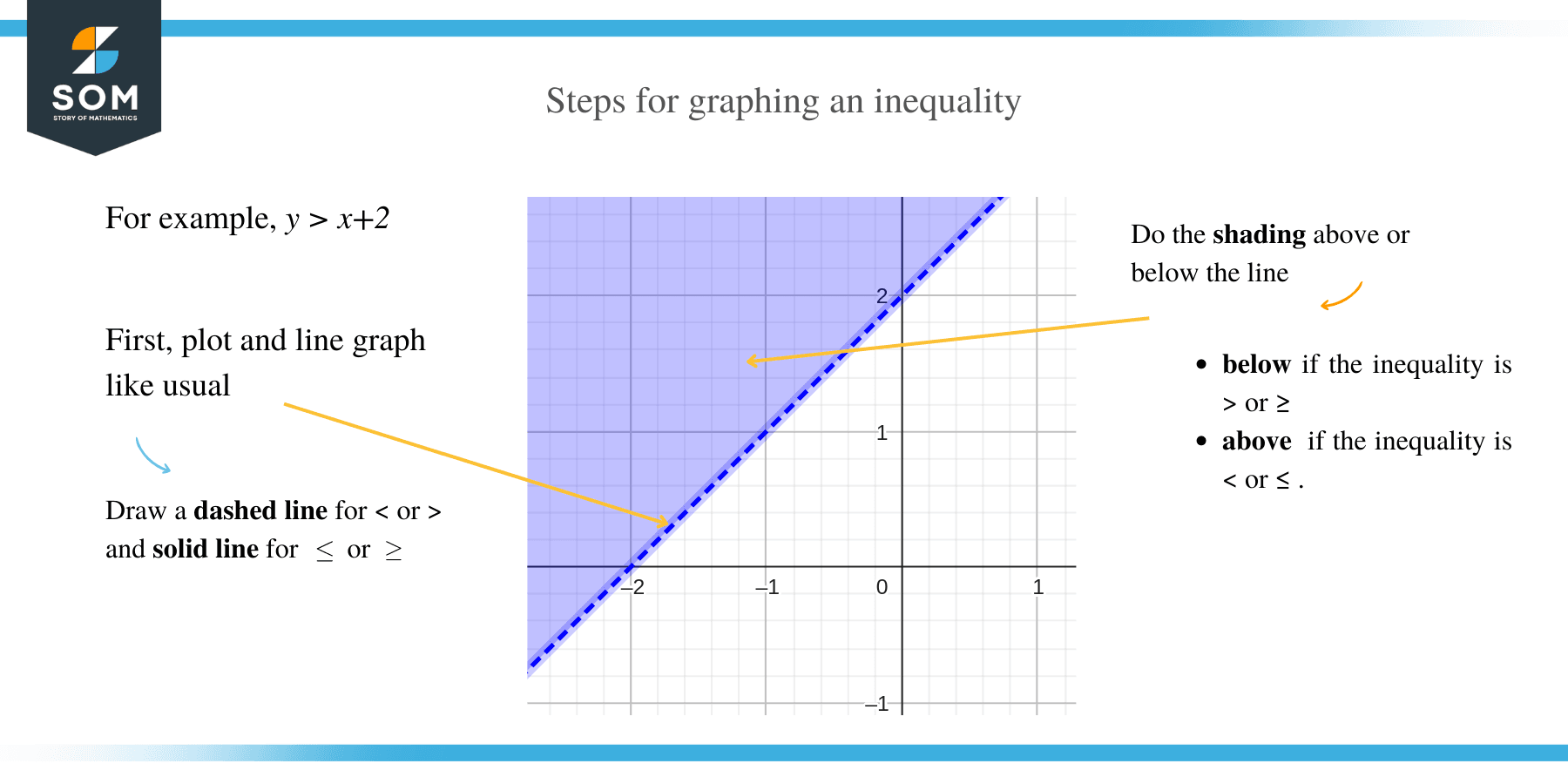
The following are the steps for graphing an inequality:

• Given an inequality equation, make y the subject of the formula. For example, y > x + 2
• Substitute the inequality sign with an equal sign and choose arbitrary values for either y or x.
• Plot and a line graph for these arbitrary values of x and y.
• Remember to draw a solid line if the inequality symbol is either ≤ or ≥ and a dashed line for < or >.
• Do the shading above and below the line if the inequality is > or ≥ and < or ≤ respectively.

How to Solve Linear Inequalities by Graphing?

Solving linear inequalities by graphing is really simple. Follow the above steps to draw the inequalities. Once drawn, the shaded area is a solution to that inequality. If there is more than one inequality, then the common shaded area is a solution to inequalities.

Let’s understand this concept with the help of the examples below.

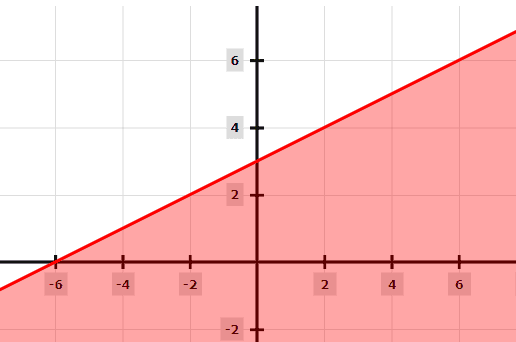
Example 1

2y − x ≤ 6

Solution

To graph, this inequality, start by making y the subject of the formula.

Adding x to both sides gives;

2y ≤ x + 6

Divide both sides by 2;

y ≤ x/2 + 3

Now plot the equation of y = x/2 + 3 as a solid line because of the ≤ sign. The shade below the line because of the ≤ sign.

Example 2

y/2 + 2 > x

Solution

Make y the subject of the formula.

Subtract both sides by 2;

y/2 > x − 2

Multiply both sides by 2 to eliminate the fraction:

y > 2x − 4

Now, because of the > sign, plot a dashed line of y = 2x − 4.

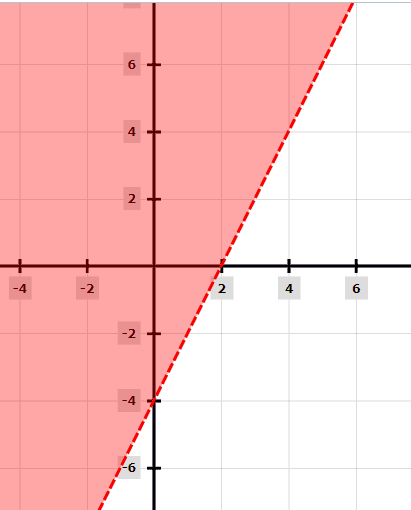
Example 3

Solve the following inequality by graphing: 2x – 3y ≥ 6

Solution

The first is to make y the subject of the line 2x – 3y ≥ 6.

Subtract 2x from both sides of the equation.

2x – 2x – 3y ≥ 6 – 2x

-3y ≥ 6 – 2x

Divide both sides by -3 and reverse the sign.

y ≤ 2x/3 -2

Now draw a graph of y = 2x/3 – 2 and shade below the line.

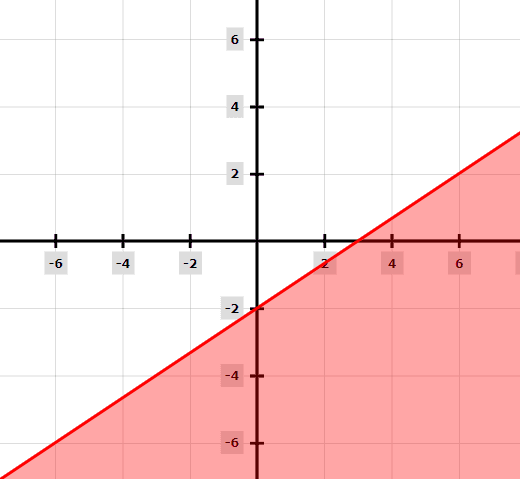
Example 4

x + y < 1

Solution

Rewrite the equation x + y = 1 to make y the subject of the formula. Because the inequality sign is <, we will draw our graph with a dotted line.

After drawing the dotted line, we shade above the line because of the < sign.

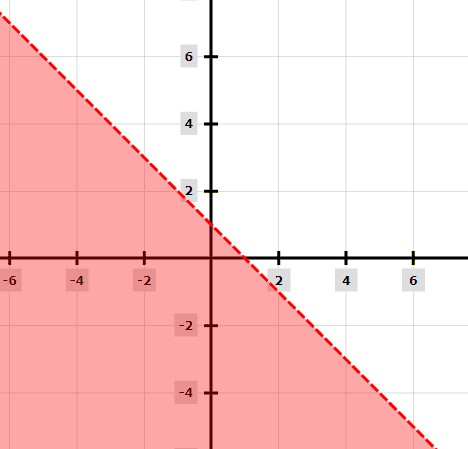
Example 5

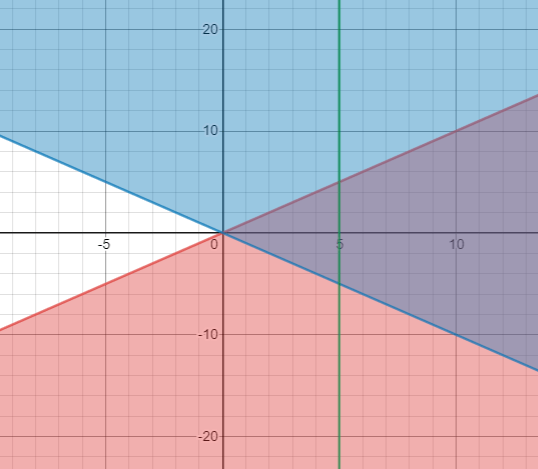
Find the graphical solution of the following inequalities:

y ≤ x

y ≥ -x

x = 5

Solution

Draw all the inequalities.

Red represents y ≤ x

Blue represents y ≥ -x

Green represents line x = 5

The common shaded area (can be seen clearly) is the graphical solution to these inequalities.