Harmonic series – Properties, Formula, and Divergence

Harmonic series is one of the first three series you’ll be introduced to in your Algebra class. This particular series is significant in music theory, and in the next section, you’ll understand why. For now, here’s a quick recap on what makes the harmonic series unique.

A harmonic series is a series that contains the sum of terms that are the reciprocals of an arithmetic series’ terms.

This article will explore this unique series and understand how they behave as an infinite series. We’ll also understand whether the series diverges or converges using the different tests we’ve learned in the past.

• Understand how arithmetic sequence (and series) can be used to define harmonic series.
• Make sure you know the difference between convergent and divergent.
• Review the different tests we can apply to confirm convergence and divergence.

Have we piqued your curiosity about the harmonic series yet? Why don’t we begin by refreshing what makes up a harmonic series?

What is a harmonic series?                

Before we dive right into the definition of a harmonic series, check out this quick visualization on how a harmonic series’ terms progress.

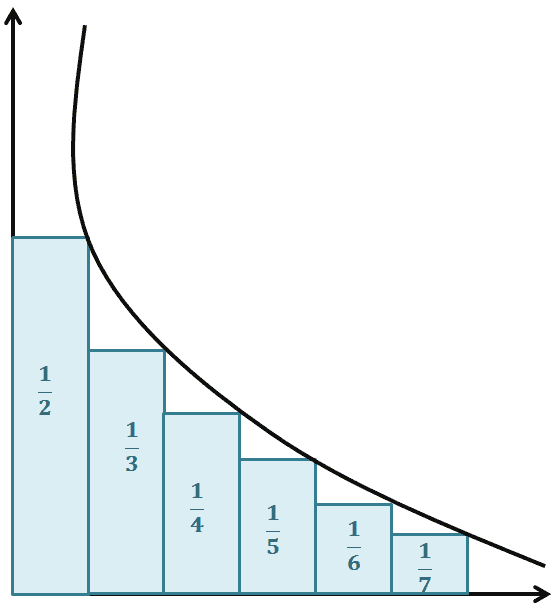
Harmonic sequence and series come hand in hand. In fact, the harmonic series is the total sum of an infinite harmonic sequence, so if we want to learn about harmonic series, we should review what we know about harmonic sequences.

To better understand this, here are two important concepts to take away from the graph shown above.

• The terms, $\left\{\dfrac{1}{2}, \dfrac{1}{3}, \dfrac{1}{4}, \dfrac{1}{5}, \dfrac{1}{6}, \dfrac{1}{7}, …\right\}$, are part of a harmonic sequence.
• The sum of terms,$ \dfrac{1}{2} +\dfrac{1}{3}+ \dfrac{1}{4}+ \dfrac{1}{5}+ \dfrac{1}{6}, \dfrac{1}{7}+ …$, is an example of harmonic series.

Let’s go ahead and formally define harmonic sequence and series.

Harmonic series definition

Harmonic sequences are sequences that contain terms that are the reciprocals of an arithmetic sequence’s terms.

Let’s say we have an arithmetic sequence with an initial term of $a$ and a common difference of $d$; we have the following terms that form the arithmetic series as shown below.

\begin{aligned}\{a , (a + d) , (a + 2d) , … , [a + (n – 1)d]\}\end{aligned}

This means that the terms of the harmonic sequence will be as shown below.

 \begin{aligned}\left\{\dfrac{1}{a} , \dfrac{1}{(a + d)} , \dfrac{1}{(a + 2d)}, … , \dfrac{1}{[a + (n – 1)d]}\right\}\end{aligned}

This shows that the denominator of a harmonic sequence’s terms will share a common difference between two consecutive terms.

Now, when we talk about harmonic series, we refer to the sum of the terms of a harmonic sequence.

Let’s use this definition, and the expressions have shown above to find the algebraic expressions and formula for a harmonic series.

Harmonic series formula

Since the sum for the arithmetic can be expressed as $S_n = a  +  (a + d) +(a + 2d) + … + [a + (n – 1)d]$. This means that the sum of the harmonic series is as shown below.

\begin{aligned}S_n &= \dfrac{1}{a} + \dfrac{1}{(a + d)} + \dfrac{1}{(a + 2d)}+ …+ \dfrac{1}{[a + (n – 1)d]}\end{aligned}

This means that the nth term of a harmonic series is equal to $\dfrac{1}{a + (n – 1)d}$.

It can be shown that the sum of the harmonic series can be approximated in terms of $a$, $d$, and $n$, as shown below.

\begin{aligned}S_n &\approx \dfrac{1}{d} \ln \left(\dfrac{2a + (2n – 1)d}{2a – d}\right)\end{aligned}

Note that this is only possible when $2a \neq d$ and $d \neq 0$.

Does harmonic series convergence exist?          

One of the first tests that we learned is the nth term test. Recall that when we have $ \sum\limits_{n=1}^{\infty} a_n$, if $\lim_{n \rightarrow \infty} a_n \neq 0$, the series is divergent.

Let’s see what happens when we have $\sum\limits_{n=1}^{\infty}\dfrac{1}{n}$, we can check the series by finding the limit of $\dfrac{1}{n}$ as $n$ approaches infinity.

\begin{aligned}\lim_{n \rightarrow \infty} \dfrac{1}{n} &= \lim_{n \rightarrow \infty}\dfrac{1}{\infty} \\&= 0\end{aligned}

Does this mean that the harmonic series is convergent? Remember that in the nth term test, a result of $0$ does not guarantee convergence.

We can also further establish that this is series is not absolutely convergent by utilizing the comparison test as discussed in the next section.

How to prove harmonic series divergence?                

What if we have an infinite harmonic series? How does the sum behave as we add more terms to the series?

Let’s say we have $ \sum\limits_{n=1}^{\infty}\dfrac{1}{n}$, we can try writing down the first terms and see how their sums progress.

From these tables of values, we can see that the partial sums increase as more terms are added. Intuition tells us that the harmonic series might be divergent instead. We use different tests to prove this, but why don’t we apply the comparison test for this section?

Recall that when we have $0 \leq a_n \leq b_n$ and if $\sum_{n=1}^{\infty}a_n$ is divergent, the series, $\sum_{n=1}^{\infty}b_n$, is also divergent.

Let’s say we have $a_n = \dfrac{1}{n}$ and $b_n = n$, it’s clear that $a_n$ will always be less than or equal to $n$ when $n$ is positive.

Since $\sum_{n=1}^{\infty}b_n$ is divergent (and definitely not convergent), we can say that the harmonic series, $\sum_{n=1}^{\infty}a_n$, is also divergent.

Why don’t we apply everything that we learned so far – from finding the terms of a harmonic series, finding the sum of the series, and prove the divergence of a harmonic series?

Example 1

The first and the seventh terms of a harmonic sequence are $\dfrac{1}{6}$ and $\dfrac{1}{12}$. Find the five terms in between these two terms.

Solution

We can go back to the definition of harmonic sequence- it contains the resulting terms when we take the reciprocal of an arithmetic sequence’s terms.

This means that the arithmetic sequence we’re basing these on will have the first term of $6$ and the seventh term of $12$.

The common difference of this sequence will be equal to $\dfrac{12 – 6}{6} = 1$, so the next five terms can be determined by adding $1$ to the previous term.

\begin{aligned}a_1 &= 6\\a_2&= 7\\ a_3 &= 8\\a_4 &= 9\\a_5 &= 10\\a_6 &= 11\\a_7 &= 12\end{aligned}

Now that we have all the terms of the arithmetic sequence, we take the terms’ reciprocals to find the missing five terms of our harmonic sequence.

Hence, we have five terms of harmonic series: $\left\{\dfrac{1}{7}, \dfrac{1}{8}, \dfrac{1}{9}, \dfrac{1}{8},\dfrac{1}{9},\dfrac{1}{10},\dfrac{1}{11} \right\}$.

Example 2

Fill in the blanks to make the following statements true.

   a. The harmonic series is a _____________ series.
   b. The limit of the nth term of a harmonic series as it approaches infinity is equal to ___________.

   c. The partial sum of the terms of a harmonic series gets ___________as the series include more terms.

Solution

As we have proven using the comparison test, the harmonic series such as $\sum_{n=1}^{\infty}\dfrac{1}{n}$ is divergent. We can use any divergent series and with an nth term larger than $\dfrac{1}{n}$ to prove the divergence of this series.

The nth term of the harmonic series in general is equivalent to $\dfrac{1}{a + (n – 1)d}$, where $a$ and $d$ are constants. We can evaluate $\lim_{n\rightarrow\infty} a_n$ as shown below.

\begin{aligned}\lim_{n\rightarrow \infty}\dfrac{1}{a + (n – 1)d} &= \lim_{n \rightarrow \infty} \dfrac{1}{\infty}\\&= 0\end{aligned}

This shows that the limit of the nth terms is equal to zero as we approach infinity.

From the table of values that we have in the earlier section, we can see that its partial sum increases as we add more terms to the series.

This also makes sense since the more terms we add, the closer the series is to approaching infinity.

Example 3

Given that $\left\{\dfrac{1}{8}, \dfrac{1}{10}, \dfrac{1}{12}, ….\right\}$ is a harmonic series, answer the following questions:

   a. What are the next three terms in the series?
   b. Find the sum of the first six terms of this harmonic series.
   c. What is the expression for the nth term of the series?
   d. Is this series divergent or convergent? Justify your answer.

Solution

Observing the denominators, $8 \rightarrow 10 \rightarrow 12$, we can see that the common difference, $d$, is equal to $2$. This means that we can find the next two terms by simply adding the denominators by $2$ each time.

\begin{aligned}a_4 &= \dfrac{1}{14}\\a_5 &= \dfrac{1}{16}\\a_6 &= \dfrac{1}{18} \end{aligned}

a. Hence, the next three terms of the series are $\dfrac{1}{14}$, $\dfrac{1}{16}$, and $\dfrac{1}{18}$.

Adding all six terms, we have:

 \begin{aligned}S_6 &= \dfrac{1}{8} + \dfrac{1}{10} + \dfrac{1}{12}+ \dfrac{1}{14} + \dfrac{1}{16} + \dfrac{1}{18}\\&= \dfrac{2509}{5040}\\&\approx 0.50\end{aligned}

b. The sum of the six terms are approximately equal to $0.50$.

Since we have $a = 8$ and $d = 2$, we can express the nth term of this series using the formula, $a_n = \dfrac{1}{a + (n – 1)d}$.

\begin{aligned}a_n &= \dfrac{1}{8 + (n – 1)2}\\&= \dfrac{1}{8 + 2n – 2}\\&= \dfrac{1}{2n + 6} \end{aligned}

c. The nth term of the harmonic series can be expressed as $\dfrac{1}{2n + 6}$.

Let’s use the comparison test to check whether the series is either divergent or convergent.

Observe that when $n$ is positive, $2n$ will always be smaller than $2n + 6$. Also, $n$ will always be smaller than $2n$.

When we take their reciprocals, the inequality will reverse since the smaller the denominator, the bigger the fraction.

\begin{aligned}n < 2n < 2n + 6\\ \dfrac{1}{n} > \dfrac{1}{2n} > \dfrac{1}{2n + 6}\end{aligned}

Why is this important? Because we can use $\sum_{n=1}^{\infty}\dfrac{1}{n}$ to show that $\sum_{n=1}^{\infty}\dfrac{1}{2n + 6}$ is divergent. Recall that when we have $0 \leq a_n \leq b_n$ and if $\sum_{n=1}^{\infty}a_n$ is divergent, the series, $\sum_{n=1}^{\infty}b_n$, is also divergent.

• We’ve shown in the past that the harmonic series, $\sum_{n=1}^{\infty} \dfrac{1}{n}$, is a divergent series.
• Since $\dfrac{1}{n} > \dfrac{1}{2n + 6}$, we can say that the series $\sum_{n=1}^{\infty} \dfrac{1}{2n + 6}$, is also divergent.

d. This justifies our answer – that the given series is divergent.