- Home
- >
- Horizontal asymptote – Properties, Graphs, and Examples
JUMP TO TOPIC
Horizontal Asymptote – Properties, Graphs, and Examples
 When given a rational function’s graph, you might notice those horizontal lines (normally dashed lines). These are the horizontal asymptotes of the function – knowing these values can help us understand the function’s restricted values.
When given a rational function’s graph, you might notice those horizontal lines (normally dashed lines). These are the horizontal asymptotes of the function – knowing these values can help us understand the function’s restricted values.
Horizontal asymptotes of a function help us understand the behaviors of the function when the input value is significantly large and small.
Many functions may contain horizontal asymptotes, but this article will use rational functions when discussing horizontal asymptotes.
It’s best to make sure you have your notes on rational functions, or you can also check out this article we wrote about rational functions.
Understanding horizontal asymptotes can help us understand the behavior of the function’s graph as they extend on both the negative and positive sides. We can begin by understanding what horizontal asymptotes signify.
What is a horizontal asymptote?
A function’s horizontal asymptotes represent the values of $f(x)$ when $x$ is significantly small or significantly large. They also represent the value of the function as $x \rightarrow \infty$ and $x \rightarrow -\infty$.
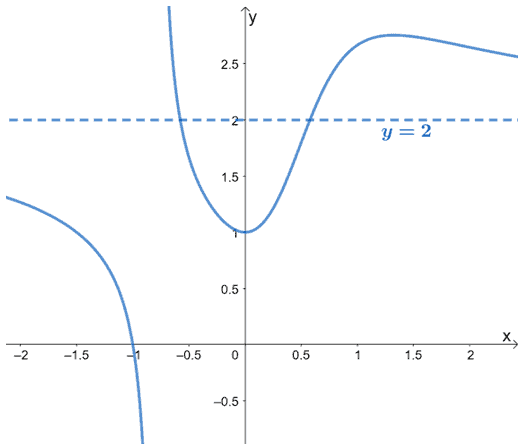
The graph above shows a rational function that has a horizontal asymptote at $y = 2$.
In general, the equation of horizontal asymptotes are represented by $y = a$, where $a$ is the value of $y$ when $x \rightarrow \pm \infty$. These values also represent the value that the function may never reach.
In the graph, these are represented by horizontal lines – most of the time, horizontal asymptotes are represented by dashed lines. Notice how the graph from our examples passes through its horizontal asymptote?
That’s the difference between vertical and horizontal asymptotes: a function’s curve can never pass through its vertical asymptote, but it is possible for it to pass through its horizontal asymptote at some points.
How to find the horizontal asymptote?
In general, we can find the horizontal asymptote of a function by determining the function’s restricted output values. If you’ve already learned about the limits of rational functions and limits of other functions, the horizontal asymptote is simply the value returned by evaluating $\lim_{x \rightarrow \infty} f(x)$.
Rational functions may have three possible results when we try to find their horizontal asymptotes. As with their limits, the horizontal asymptotes of functions will depend on the numerator and the denominator’s degree.
Horizontal asymptote rules in rational functions
As mentioned, we have three rules to remember when finding the horizontal asymptotes of rational functions. Let’s say we have the rational function in standard form, $f(x) = f(x)=\dfrac{a_nx^n + a_{n-1}x^{n-1}+ … + a_o}{b_mx^m + b_{m-1}x^{m-1}+ … + b_o}$, where $a_nx^n$ and $ b_mx^m$ are the leading coefficients of the numerator and denominator, respectively.
Rule 1: When the degree of the numerator is less than the degree of the denominator, the $\boldsymbol{x}$-axis is the horizontal asymptote.
Let’s observe this with $f(x) = \dfrac{x}{x^2 – 1}$ and check the values when $x \rightarrow -\infty$ and $x \rightarrow \infty$.
$\boldsymbol{x}$ | $\boldsymbol{f(x)}$ |
$-10000$ | $-0.0001$ |
$-1000$ | $-0.001$ |
$-100$ | $0.01$ |
$100$ | $0.01$ |
$1000$ | $0.001$ |
$10000$ | $0.0001$ |
We can see that as $x$ becomes significantly larger and smaller, $f(x)$ approaches zero. This means that its asymptote is the $y = 0$ or the $x$-axis.
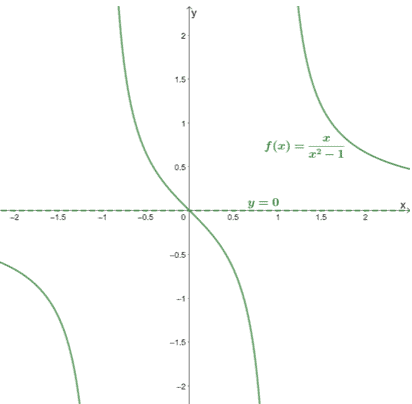
Seeing the graph of $f(x)$, we can confirm that its horizontal asymptote lies along the $x$-axis. In general, as long as $n < m$, the horizontal of the function is the $x$-axis.
Rule 2: When the degree of the numerator is equal to the degree of the denominator, find the function’s horizontal asymptote by dividing the numerator’s leading coefficient by the denominator’s.
A good example of a function having the same degree on both its numerator and denominator is $f(x) = \dfrac{6x^2 – 1}{3x^2 + 1}$. We can also observe the values of $f(x)$ at values of $x$ that are significantly large or small.
$\boldsymbol{x}$ | $\boldsymbol{f(x)}$ |
$-10000$ | $2$ |
$-1000$ | $2$ |
$-100$ | $1.9999$ |
$100$ | $1.9999$ |
$1000$ | $2$ |
$10000$ | $2$ |
We can see that as $x$ becomes significantly larger and smaller, $f(x)$ approaches $2$. This means that its asymptote is the $y =2$. We can confirm this by dividing the leading coefficients of $y =\dfrac{6}{3}= 2$.
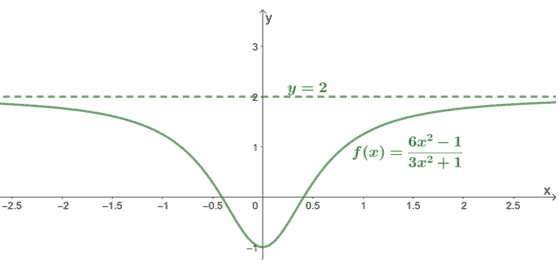
The graph of $f(x)$, as shown above, confirms this since both sides of the function approaches $2$. The general rule is that when $n = m$, the horizontal asymptote of the function is $y = \dfrac{a_n}{b_m}$.
Rule 3: When the degree of the numerator is greater than the degree of the denominator, the function has no horizontal asymptote.
Let’s observe this with $f(x) = \dfrac{x^3}{x^2+ 1}$ and check the values when $x \rightarrow -\infty$ and $x \rightarrow \infty$.
$\boldsymbol{x}$ | $\boldsymbol{f(x)}$ |
$-10000$ | $-9999.9999$ |
$-1000$ | $-999.999$ |
$-100$ | $-99.99$ |
$100$ | $99.99$ |
$1000$ | $999.999$ |
$10000$ | $9999.9999$ |
From this, we can see that the values do not approach a common value, further confirming what we know: $f(x)$ has no horizontal asymptotes. In fact, it will have an oblique asymptote instead.
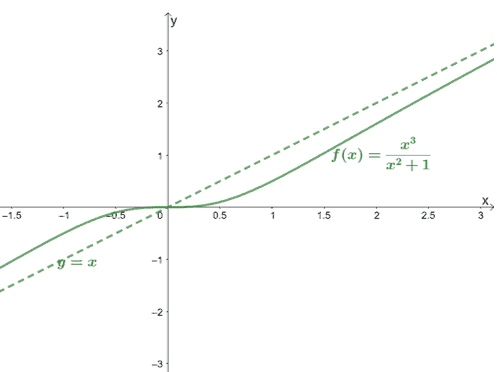
The rule applies for all functions that have $n > m$. The graph of $f(x)$ also shows that when $n>m$, we actually have a slanted or oblique asymptote instead.
How to graph horizontal asymptote?
Now that we know how to find the horizontal asymptotes of a function, it’s time that we learn how to graph and integrate them on a function’s graph.
- Since the general form of horizontal asymptotes is $y = a$, the horizontal asymptote will be a horizontal line (hence, its name).
- Graph a horizontal line that passes through $(0, a)$ and extends on both sides.
- When given the rational function’s graph, keep in mind that it’s okay for the graph to pass through the horizontal asymptote.
Let’s try to graph the horizontal asymptote of $f(x) = \dfrac{2x- 1}{3x + 2}$. Since the degrees of both the numerator and denominator are equal, its horizontal asymptote is equal to $y = \dfrac{2}{3}$.
We construct a dashed horizontal line that passes through the point, $\left(0, \dfrac{2}{3}\right)$. You can always construct the graph right away. The point is just a guide and helps you know the position of the horizontal line.
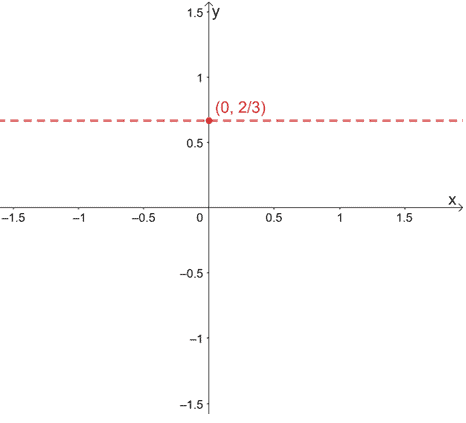
Why don’t we include the graph of $f(x)$ to show how the graph would look with the asymptote?
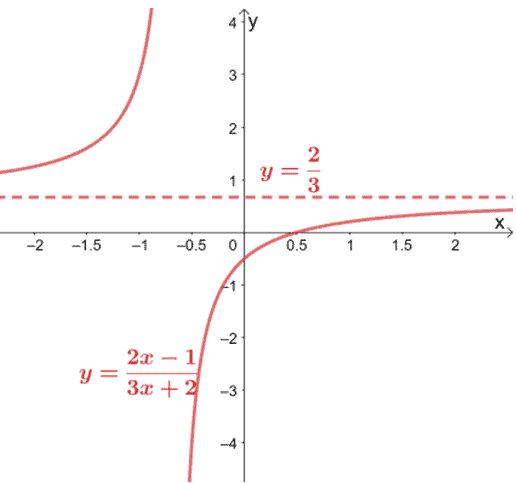
Need refresher on graphing rational functions? Don’t forget to review our tips from our previous article on rational functions. From the graph, we can also see that as $x \rightarrow \pm \infty$, $f(x) \rightarrow \dfrac{2}{3}$.
Summary of horizontal asymptote definition and properties
We’ve now extensively discussed horizontal asymptotes, so before we try out more problems involving horizontal asymptotes, why don’t we summarize what we have learned so far?
- Horizontal asymptotes represent the value of $f(x)$ when $x$ approaches positive or negative infinity.
- Its general form is $y = a$, where $a =\lim_{x \rightarrow \infty} f(x)$.
- A dashed horizontal line represents its graph.
- If $f(x)$ is a rational function, the value of $a$ or the asymptote will depend on its degree.
Degree Condition | Horizontal Asymptote |
$m < n$ | $y = 0$ or the $x$-axis |
$m = n$ | $y=\dfrac{a_n}{b_m}$ or the leading coefficients’ ratio |
$m > n$ | No horizontal asymptote |
Now, it’s time for us to use what we’ve just learned and tried out the sample problems below!
Example 1
Fill in the blanks to make the following statements true.
a. If $\lim_{x \rightarrow \infty} f(x) = -4$, this means that the horizontal asymptote of $f(x)$ is ______________.
b. If the horizontal asymptote of $g(x)$ is equal to $-5$ is, the degree of the $g(x)$’s denominator is __________ its numerator.
c. The graph of the horizontal asymptote of $h(x)$ lies along the $x$-axis. If the numerator of $h(x)$ is $-5x^3 + 4x$, its denominator’s degree must be __________.
Solution
Recall that we can also find the horizontal asymptote by finding the limit of the function as the input value approaches infinity.
a. This means that if $\lim_{x \rightarrow \infty} f(x) = -4$, so the equation for the horizontal asymptote is $\boldsymbol{y = -4}$.
b. Since $g(x)$ has a constant for its horizontal asymptote, this means that $m < n$ or the denominator must be equal to its numerator.
When the horizontal asymptote lies along the $x$-axis, the degree of the numerator must be less than its denominator’s degree.
c. Since the degree of the numerator is 3, the denominator’s degree must be less than 3.
Example 2
We’ve thoroughly discussed horizontal asymptotes from rational functions. Write down a function that contains a horizontal asymptote.
Solution
As we have mentioned in the previous sections, there a lot of functions that contain horizontal asymptotes. One example of such functions is the exponential function.
One example of a power function is the function $\boldsymbol{y = 2^{x} – 1}$. Since square roots will restrict the output values, we are expecting horizontal asymptotes as well.
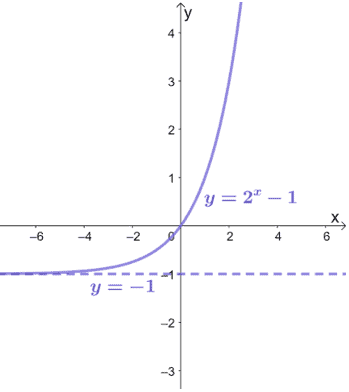
Since $2^x$ can never be zero, the value $y$ must never be $-1$. The graph above also confirms that $y = 2^{x} – 1$ has a horizontal asymptote at $y = 1$.
Example 3
Find the horizontal asymptotes of the following functions:
a. $f(x) = \dfrac{x^5 – x^4 + 1}{x^3 – 1}$
b. $g(x) = \dfrac{3x(x – 1)(x + 2)}{9x^3 + 1}$
c. $h(x) = \dfrac{(x – 1)(x^2 +1)}{5x^4 + 3x^2 – 2x + 1}$
Solution
Let’s refer to the rules of horizontal asymptotes for each of the given function.
Starting with $f(x) = \dfrac{x^5 – x^4 + 1}{x^3 – 1}$, we can see that the degree in the numerator is larger than that of the denominator.
$\begin{aligned}f(x)&=\dfrac{x^{\boldsymbol{5}} – x^4 + 1}{x^{\boldsymbol{3}} – 1}\\\boldsymbol{5} &>\boldsymbol{3}\end{aligned}$
a. This means that $\boldsymbol{f(x)}$ has no horizontal asymptote.
Since the numerator of $g(x)$ is in factored form, let’s multiply the leading terms to find its leading coefficient’s degree: $3x \cdot x \cdot x= 3x^3$. The denominator has $3$ as its degree, so their horizontal asymptote can be determined by dividing $3x^3$ by $9x^3$.
$\begin{aligned}y&=\dfrac{3}{9}\\&=\dfrac{1}{3}\end{aligned}$
b. Hence, $g(x)$ has a horizontal asymptote at $\boldsymbol{y = \dfrac{1}{3}}$.
Similar with $g(x)$, let’s find the leading coefficient of $h(x)$’s numerator first: $x \cdot x^2 = x^3$.
Since the numerator’s degree is less than its denominator, its horizontal asymptote will be the $\boldsymbol{x}$-axis.
c. This means that the horizontal asymptote of $\boldsymbol{h(x)}$ is $\boldsymbol{y=0}$.
Example 4
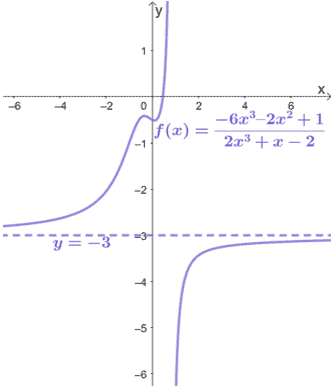
Given that $f(x) = \dfrac{-6x^3 – 2x^2 + 1}{2x^3 + x – 2}$, describe its horizontal asymptote and graph the horizontal asymptote on the given graph of $f(x)$.
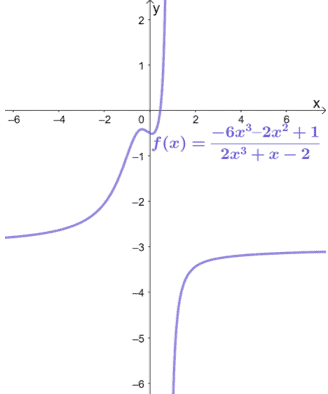
Solution
Let’s first observe the degrees of the leading terms found in $f(x)$.
$\begin{aligned}f(x)&= \dfrac{-6x^\boldsymbol{3} – 2x^2 + 1}{2x^\boldsymbol{3} + x – 2}\\ 3&=3\end{aligned}$
Since the degrees are equal, we can divide the leading coefficients $\dfrac{-6}{2}$. Hence, we have $\boldsymbol{y = -3}$.
Graph the horizontal asymptote by graphing a dashed horizontal line that passes through the point $(0, -3)$.
Example 5
Jennifer is running a small shop, and she is currently offering a great deal on her handcrafted soaps. If you buy one bar of soap for $\$2.50$, then additional bars will only cost $\$1.50$ each. As a customer purchases more and more bars, what is the average cost per bar of soap?
Solution
Horizontal asymptotes can also help us find an approximate of the output value as the input becomes significantly higher or smaller.
Let $s$ represent the number of soaps a customer orders from Jennifer’s shop.
The first bar will cost $\$2.50$, and the rest of the $(s – 1)$ bars will cost $\$1.50$ each. This means that the total cost of purchasing $s$ bars will be $2.50 + 1.50(s – 1)$ dollars.
If we let $A(s)$ represent the average cost of purchasing $s$ bars, we can find its expression by dividing the cost by $s$.
$\begin{aligned} A(s) &= \dfrac{2.50 + 1.50(s-1)}{s}\\&=\dfrac{2.50 + 1.50s – 1.50}{s}\\&=\dfrac{1 + 1.50s}{s}\end{aligned}$
Now, to find the value when $s \rightarrow \infty$, we find the horizontal asymptote of $A(s)$. Since the numerator and denominator of $A(s)$ share the same degree, the horizontal asymptote of $A(s)$ is equal to $\dfrac{1.50}{1} = 1.50$.
This means that as the customer orders more bars of soap, the average cost of each bar approaches $\boldsymbol{\$ 1.50}$.
Practice Questions
![]()
Open Problems
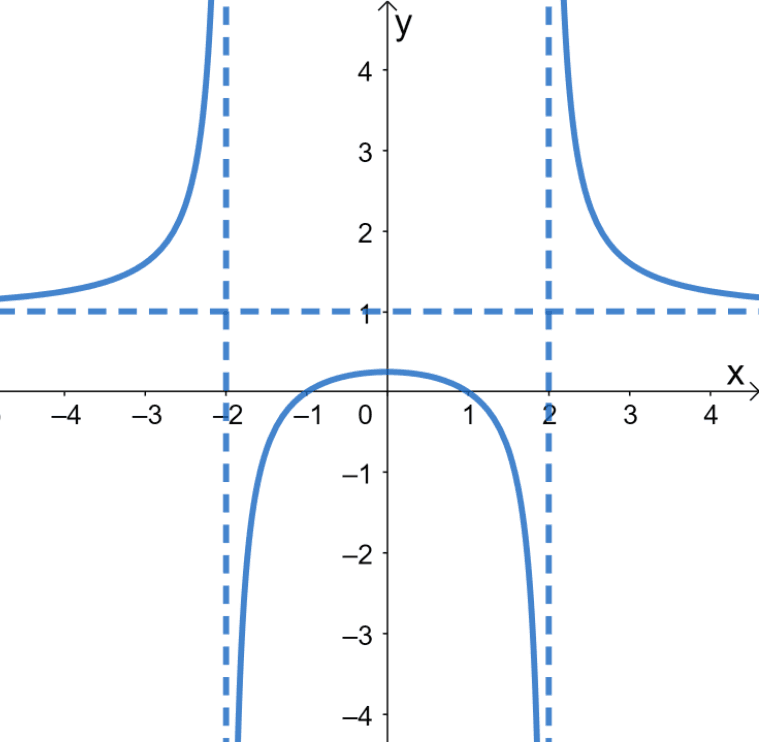
Complete the table shown below by finding the values of $f(x) = \dfrac{(x-1)(x+1)}{x^2 – 4}$ at the different values of $x$.
$\boldsymbol{x}$ | $\boldsymbol{f(x)}$ |
$-10000$ | |
$-1000$ | |
$-100$ | |
$100$ | |
$1000$ | |
$10000$ |
a. Based from the table of values, what is the value of $\lim_{x \rightarrow \infty} f(x)$?
b. Using your answer from the previous question, what is the horizontal asymptote of $f(x)$?
c. Graph the function and its horizontal asymptote.
Open Problem Solutions
$\boldsymbol{x}$ | $\boldsymbol{f(x)}$ |
$-10000$ | $\dfrac{33333333}{33333332}$ |
$-1000$ | $\dfrac{333333}{333332}$ |
$-100$ | $\dfrac{3333}{3332}$ |
$100$ | $\dfrac{3333}{3332}$ |
$1000$ | $\dfrac{333333}{333332}$ |
$10000$ | $\dfrac{33333333}{33333332}$ |
a. $\lim_{x \rightarrow \infty} f(x) = 1$
b. $y = 1$
c.
Images/mathematical drawings are created with GeoGebra.
