- Home
- >
- Horizontal Stretch – Properties, Graph, & Examples
JUMP TO TOPIC
Horizontal Stretch -Properties, Graph, & Examples
 You may already have encountered graphs that look alike but share different widths. These functions may have been horizontally stretched using a base function. Horizontal stretches are among the most applied transformation techniques when graphing functions, so it’s best to understand its definition.
You may already have encountered graphs that look alike but share different widths. These functions may have been horizontally stretched using a base function. Horizontal stretches are among the most applied transformation techniques when graphing functions, so it’s best to understand its definition.
Horizontal stretches happen when a base graph is widened along the x-axis and away from the y-axis.
Learning how we can stretch graphs horizontally can help us understand the family of functions’ graphs. We can also learn how to speed up graphing new functions based on the scale factors applied.
Make sure to review your knowledge of parent functions, translations, and vertical stretches before moving to the next section.
- Understanding the common parent functions we might encounter.
- Refresh your knowledge of vertical and horizontal transformations.
- Review how we apply vertical stretches.
These linked articles may help you refresh your knowledge, and when you’re ready, let’s go ahead and learn more about horizontal stretching.
What is a horizontal stretch?
We can apply horizontal stretch to a function by multiplying its input values by a scale factor, a, where 0 < 1/a < 1. What does this mean for functions such as f(x)? When 1/a is multiplied to x, f(x)’s graph stretches horizontally by a scale factor of a.
Let’s go ahead and look at how f(x) = x2 will be affected by a scale factor of 1/2 and 1/3.
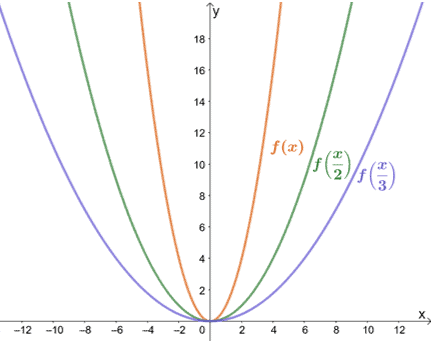
As we have expected, the graph stretches by a factor of 2 and 3. Notice how the y-values remain the same? This is true for all horizontal stretches. The graph only stretches away from the y-axis when we horizontally stretch a graph.
Horizontal stretch on other functions will exhibit similar properties. Let’s say we have f(x) = |x|, if this function’s graph is to be stretched horizontally to attain g(x), the new function’s expression can be expressed as |1/3 ∙ x| = |x/3|.
Why don’t we compare some values from both functions?
| x | -2 | -1 | 0 | 1 | 2 |
| f(x) = |x| | 2 | 1 | 0 | 1 | 2 |
We also expect all its x-coordinates to increase by 3. When we do this, the output values will remain the same.
| x | -6 | -3 | 0 | 3 | 6 |
| g(x) = |x/3| | 2 | 1 | 0 | 1 | 2 |
What does this mean for the coordinates of the new function’s graph? If the function f(x) passes through (m, n) and is stretched horizontally by a factor of 1/a, the new function will pass through (am, n).
How to horizontally stretch a function?
Now that we’ve learned about horizontal stretches and how they affect a base function, it’s time that we apply these on functions’ graphs. Before we start stretching functions horizontally by a certain factor, remember these pointers to stretch graphs faster horizontally:
- Only stretch the base of the graph horizontally so that the y-coordinates would remain in the same position.
- Since the y-coordinates will remain the same, the y-intercept stays the same as well.
- Make sure to double-check critical points on the graph, such as its intercepts, maximum points, and more.
- See if the coordinate points are scaled correctly as well.
Let’s use the table of values shown in the previous section to graph both y = |x| and y = |x/3| to visualize the effects of a horizontal stretch on a graph.
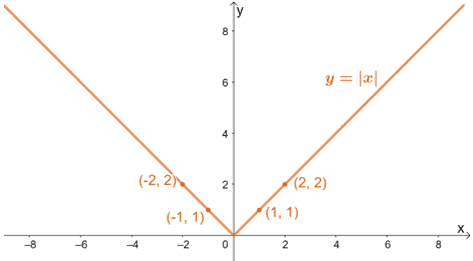
As we have discussed, we’re expecting the graphs to stretch along the base with the values for y remaining constant.
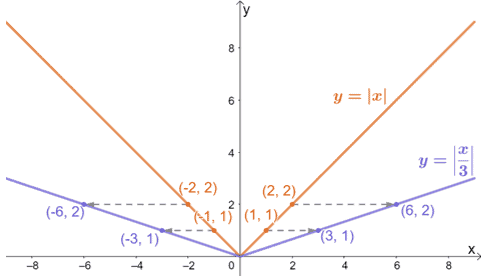
To attain y = |x/3|, we stretch the parent function y = |x| by a factor of 3. The graph shown above confirms this, and we can apply the same process when horizontally stretching the graphs of other functions.
Ready to graph more functions and apply horizontal stretches? Let’s summarize what we have learned so far first before we try out more questions.
Summary of horizontal stretch definition and properties
Here are some important pointers to remember when answering problems and graphing functions that involve horizontal stretches:
- We can only horizontally stretch a graph by a factor of 1/a when the input value is also increased by a.
- When f(x) is stretched horizontally to f(ax), multiply the x-coordinates by a.
- Retain the y-intercepts’ position.
- The resulting function will have the same range but may have a different domain.
- Given a point (m, n), it becomes (am, n) when stretched horizontally.
Let’s always go back to these five-pointers when in doubt. Being able to master the technique of horizontally stretching graphs can help us graph functions faster and understand their behavior.
Are you ready to test your knowledge? Let’s go ahead and try out some of these problems!
Example 1
The function, g(x), is obtained by horizontally stretching f(x) = 8x by a scale factor of 1/4. Which of the following is the correct expression for g(x)?
a. g(x) = 32x
b. g(x) =16x
c. g(x) = 2x
d. g(x) =1/2 x
Solution
Remember that when we horizontally stretch a function by 1/a, we divide the input value by a. Why don’t we apply this to the problem? We replace x with x/4 to find the expression for g(x).
g(x) = 8(x/4)
Simplifying the expression will lead to g(x) = 2x.
Example 2
Write the expressions for g(x) and h(x) in terms of f(x) given the following conditions:
a. The function g(x) is the result of f(x) being stretched horizontally by a factor of 1/5.
b. When we horizontally stretch g(x) by a scale factor of 1/2, we obtain h(x).
Solution
Let’s start with g(x). We can horizontally stretch f(x) to obtain g(x), so we divide the input value of f(x) by 5 to obtain g(x)’s expression: f(x/5).
Now that we have g(x), we can find the expression for h(x). We divide g(x)’s input value by 2. Hence, we have:
h(x) = g(x/2)
= f(x/5 ·1/2 )
= f(x/10)
This means that in terms of f(x), g(x) = f(x/5) and h(x)= f(x/10).
Example 3
The function, f(x), passes through the point (6, 4). If f(x) is horizontally stretched by a scale factor of 1/2, what would be the new x-coordinate of the point?
Solution
When we stretch a graph horizontally, we multiply the base function’s x-coordinate by the given scale factor’s denominator to find the new point lying along the same y-coordinate.
Hence, we have (6, 4) → (2 ∙ 6, 4). The new x-coordinate of the point will be (12, 4).
Example 4
The table of values for f(x) is shown below. If h(x) is the result of f(x) being horizontally stretched by a scale factor of 1/4, construct its table of values and retain the current output values.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | -6 | -4 | -2 | 0 | 2 | 4 | 6 |
Solution
When the function is stretched horizontally, we multiply the input values (for this case, it’s the values of x) by the given scale factor’s denominator.
This means that (-2, -4) will be transformed to (4∙ -2, -4) = (-8, -4). We apply the same process for the rest of the values and have h(x)’s table of values as shown below.
| x | -12 | -8 | -4 | 0 | 4 | 8 | 12 |
| h(x) | -6 | -4 | -2 | 0 | 2 | 4 | 6 |
Example 5
Observe the functions shown below. What is the relationship between f(x) and g(x)?
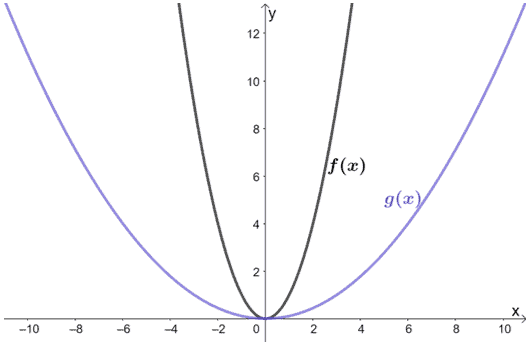
Solution
Just by looking at the graph, we can see that g(x) results from f(x) being stretched horizontally. Why don’t we inspect some points from both graphs?
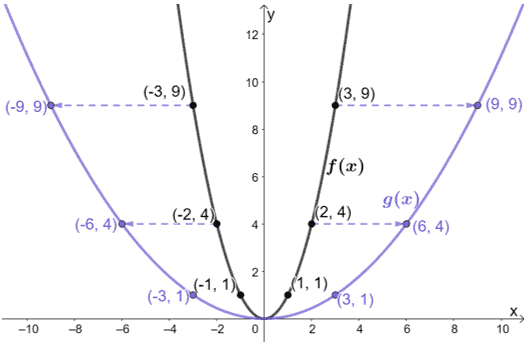
This is what happens to the points:
- (-3, 9) → (-9, 9)
- (-2, 4) → (-6, 4)
- (-1, 1) → (-3, 1)
- (0, 0) → (0, 0)
- (1, 1) → (3, 1)
- (2, 4) → (6, 4)
- (3, 9) → (9, 9)
Notice how for each case: the x-coordinates of g(x) are all three times larger than f(x). This means that the scale factor used to stretch f(x) is 1/3.
The function g(x) is the result of f(x) being horizontally stretched by a scale factor of 1/3.
Example 6
The image below shows the graph of f(x). Graph g(x) using the fact that it is the result of f(x) being stretched horizontally by a factor of 1/2. Make sure to include the new critical points for g(x).
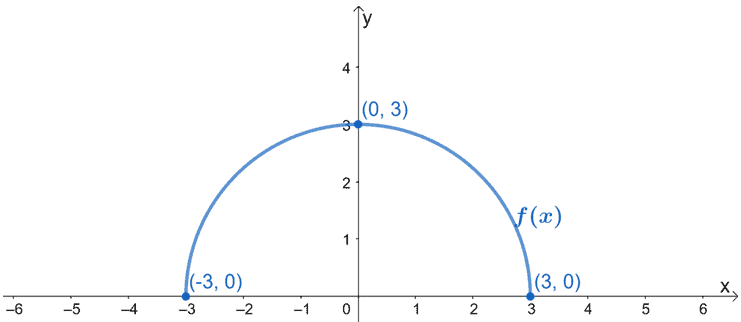
Solution
Let’s go ahead and find the new critical points of g(x) first. Since f(x) will be stretched horizontally, we’ll multiply the x-coordinates by 2. Hence, we have the following critical points:
- (-3, 0) → (-6, 0)
- (0, 3) → (0, 3)
- (3, 0) → (6, 0)
Plot these points and stretch the graph of f(x) by 3. Make sure that the y-coordinates and y-intercept remain the same.
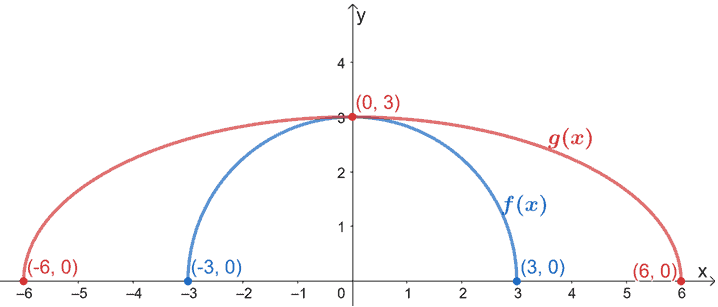
This is how the resulting graph should look like. Since g(x) is the result of f(x) being stretched horizontally, we stretch the graph of f(x) by a scale of 3.
Example 7
Describe the transformations done on the following functions shown below.
a.f(x) = x2 → g(x) = x2/9
b. m(x) = √x → n(x) = 3√(x/4)
c. p(x) = 3x – 1→ q(x) = 3x/4 – 2
Solution
If you might have noticed that some may not only exhibit horizontal stretches, you are right!
Keep in mind that we sometimes have to apply different transformation techniques for us to obtain a particular function’s expression.
First, let’s start with f(x) and g(x):
To check the scale factor applied in the input value of f(x) to attain g(x), let’s express g(x) as a perfect square: g(x) = (x/3)2 = (1/3 · x)2.
Expressing g(x) in terms of f(x), we have g(x) = f(x/3). Hence, g(x) is the result of f(x) being horizontally stretched by a scale factor of 1/3.
Moving on to m(x) and n(x):
We can see two scale factors applied to n(x): 3 on the output value and 1/4 for the input value. Applying what we know on vertical and horizontal stretches, we have n(x) = 3·m(1/4 · x). Meaning, n(x) is the result of m(x) being vertically stretched by a scale factor of 3 and horizontally stretched by a scale factor of 1/4.
Lastly, let’s observe the translations done on p(x).
q(x) = 3/4 x – 1 – 1
= 3(x/4) – 1 – 1
= p(x/4) – 1
From this, we can see that q(x) results from p(x) being stretched horizontally by a scale factor of 1/4 and translated one unit downward.
Example 8
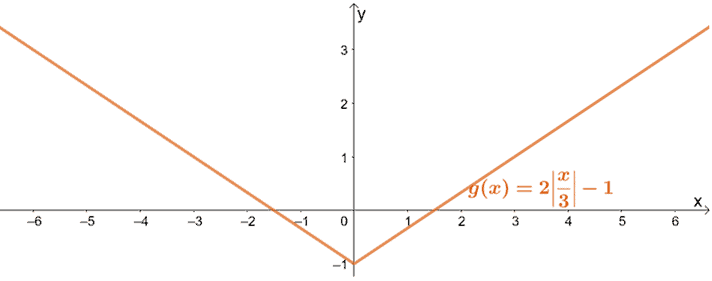
What are the transformations done on f(x) so that it results to g(x) = 2|x/3| – 1? Use the graph of f(x) shown below to guide you. Apply the transformations to graph g(x).
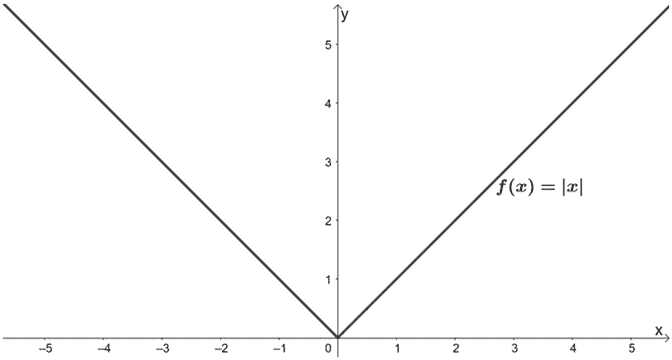
Solution
Let’s go ahead and express g(x) in terms of f(x).
g(x) = 2 · |1/3 · x| – 1
= 2· f(x/3) – 1
This means that the translations on f(x) to obtain g(x) are:
- Horizontally stretched by a scale factor of 1/3.
- Vertically stretched by a scale factor of 2.
- Translated downwards by 1 unit.
Let’s slowly apply these transformations on f(x), starting with horizontally stretching f(x).
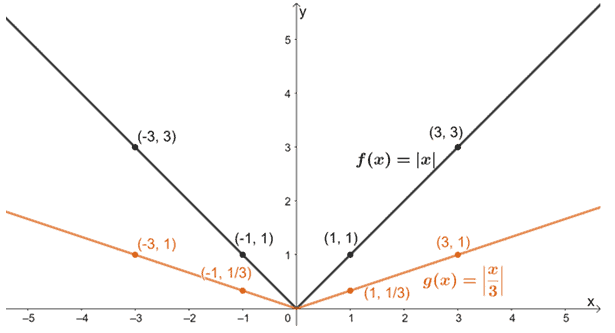
Let’s now stretch the resulting graph vertically by a scale factor of 2.
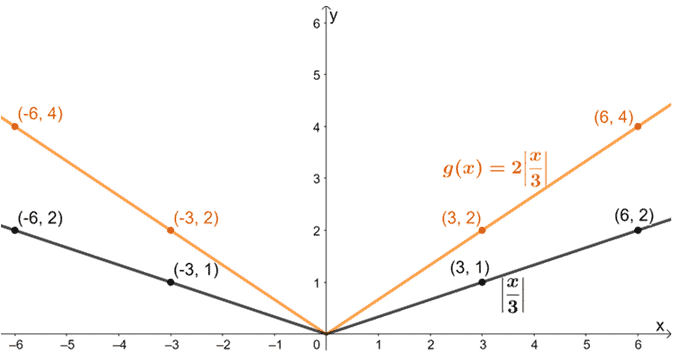
Lastly, let’s translate the graph one unit downward.
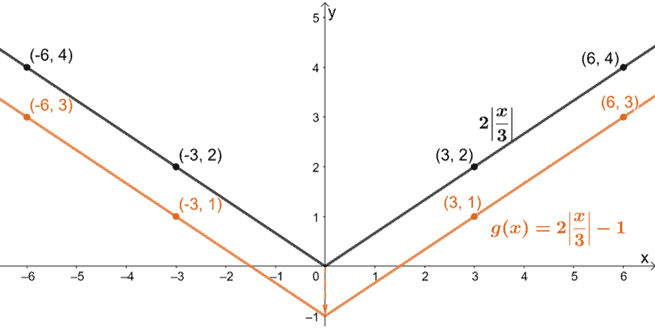
Hence, we’ve just shown how g(x) can be graphed using the parent function of absolute value functions, f(x) = |x|.
Practice Questions
![]()
Open Problems
1. The table of values for $f(x)$ is shown below. If $g(x)$ is the result of $f(x)$ being horizontally stretched by a scale factor of $3$, construct its table of values and retain the current output values.
| x | -9 | -6 | -3 | 0 | 3 | 6 | 9 |
| f(x) | -17 | -11 | -5 | 1 | 7 | 13 | 19 |
2.
The image below shows the graph of $f(x)$. Graph $h(x)$ using the fact that it is the result of $f(x)$ being stretched horizontally by a factor of $\dfrac{1}{3}$. Make sure to include the new critical points for $g(x)$.
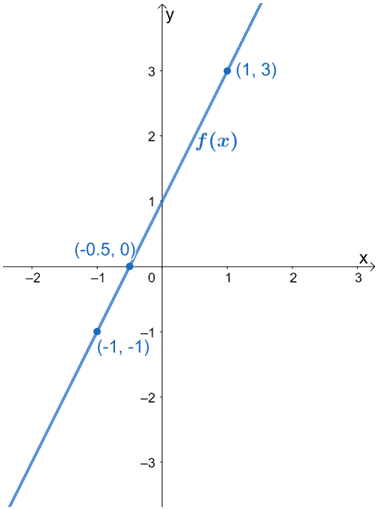
Open Problem Solutions
1.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | -17 | -11 | -5 | 1 | 7 | 13 | 19 |
2.
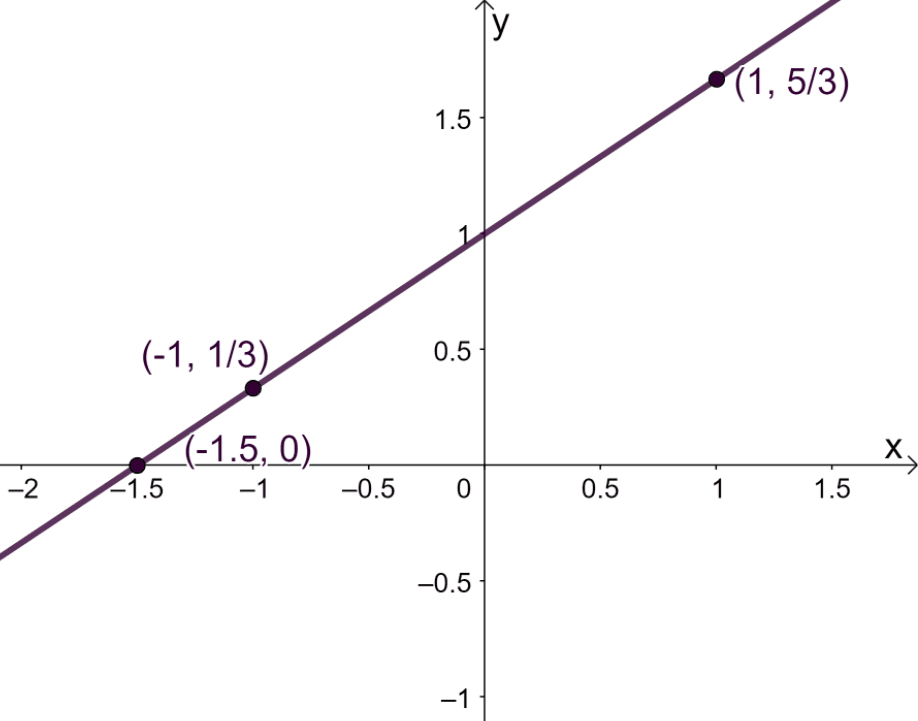
Images/mathematical drawings are created with GeoGebra.
