Integral Test – Definition, Conditions, and Examples

The integral test is an important tool kit to learn when studying series and their convergence. As we know, series and sequences are the foundations of advanced numerical analysis. This means that convergence tests such as the integral test are essential when we’re studying different types of series.

The integral test is an essential tool kit in determining whether a given series is convergent or not. This test uses a closely related improper integral to determine a series’ convergence.

Our discussion will thoroughly explore the concepts behind the integral test. We’ll cover its definition, conditions, and process and also learn when it’s best to use this convergence test. We’ll be dealing with improper integrals in this article, so keep your notes handy or head over to this link for a quick refresher.

By the end of our discussion, we’ll make sure that you can work independently and master this technique. This will be a thorough discussion, so take notes when you can.

For now, let’s go ahead and understand what makes this convergence test unique and understand how we have established the rules for the integral test.

What is the integral test?

The integral test determines whether a given series is convergent or not by comparing the series to a closely related improper integral. When $f(x)$ is continuous, positive and decreasing, within the interval $[1, \infty)$ and we define $a_n$ as $f(n)$, according to the integral test:

We’ll show you how we can establish this technique and understand the key conditions when implementing the integral test. For now, let’s observe how we can establish the integral test’ method by estimating the sum of $\sum_{n = 1}^{\infty} \dfrac{1}{n^2}$.

Finding the exact value of a series, $S_n$, is often challenging unless we’re working with a series that has been studied thoroughly in the past. This is when convergence tests such as the integral test enter.

Let’s begin by observing the series containing terms with the reciprocals of the squares of the positive integrals, $\{1,2, 3, 4, …\}$.

\begin{aligned}\sum_{n = 1}^{\infty} \dfrac{1}{n^2} &= \dfrac{1}{1^2} + \dfrac{1}{2^2} + \dfrac{1}{3^2} + \dfrac{1}{4^2}+ …\end{aligned}

We haven’t learned of a straightforward approach in the past that allows us to approximate the sum of this series’ first $n$ terms. Let us show you the table of values that the series approaches as $n$ increases (we used a computer to calculate these):

From the table of values, we can see that as $n \rightarrow$, the sum of the series, $S_n$, converges to a given value. In fact, we can confirm this geometrically by graphing the curve of $y= \dfrac{1}{x^2}$ and the rectangles representing each term’s value. This will be similar to how we construct the rectangle for the Riemann sum.

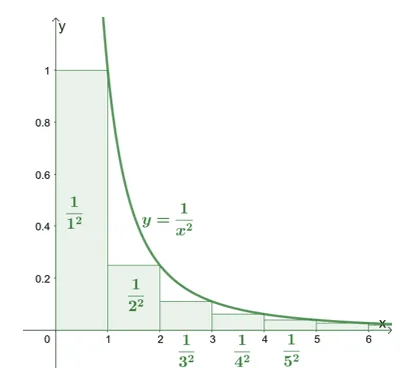
From the graph, we can see that the function converges and in addition, the sum of the rectangles’ areas will be equivalent to our original series:

\begin{aligned}\sum_{n = 1}^{\infty} \dfrac{1}{n^2} &= \dfrac{1}{1^2} + \dfrac{1}{2^2} + \dfrac{1}{3^2} + \dfrac{1}{4^2}+ …\end{aligned}

If we take out the first rectangle with an area of $\dfrac{1}{1!} = 1$ square unit, the sum of the area of the remaining rectangles will be less than the area of the curve, $y = \dfrac{1}{x^2}$, for the interval, $[1, \infty)$. Using the fundamental theorem of calculus, we can express the area of $y$ as $\int_{1}^{\infty} \dfrac{1}{x^2} \phantom{x}dx$.

\begin{aligned}\sum_{n = 1}^{\infty} \dfrac{1}{n^2} &= \dfrac{1}{1^2} + \dfrac{1}{2^2} + \dfrac{1}{3^2} + \dfrac{1}{4^2}+…+\dfrac{1}{n^2} + …< 1 + \int_{1}^{\infty} \dfrac{1}{x^2} \phantom{x}dx \end{aligned}

We’ve learned how to evaluate improper integrals in the past and we can show that $ \int_{1}^{\infty} \dfrac{1}{x^2} \phantom{x}dx = 1$. Need a refresher? Check out the calculations below.

This means that we can simplify our inequality  as shown below.

\begin{aligned}\sum_{n = 1}^{\infty} \dfrac{1}{n^2} &= \dfrac{1}{1^2} + \dfrac{1}{2^2} + \dfrac{1}{3^2} + \dfrac{1}{4^2}+…+\dfrac{1}{n^2} + …< 2 \end{aligned}

Since the series as well as its partial sums is less than $2$ and we know that $S_n$ is increasing by  $\dfrac{1}{n^2}$, the series converges.

\begin{aligned}S_{n} &= S_{n – 1} + \dfrac{1}{n^2}\\ &\Rightarrow \text{Series converges}\end{aligned}

 Through the Monotone Convergence Theorem, we can conclude that the series $\sum_{n = 1}^{\infty} \dfrac{1}{n^2}$ converges. We’ll follow the same process when confirming the convergence of series using the integral test. For now, let’s generalize the process and understand when it’s best to utilize this technique.

Integral test conditions

If the series, $\sum_{n = 1} a_n$, contains positive terms $a_n$ so that there exists a continuous, positive, and decreasing function, $f(n) = a_n$, the partial sum of the series, $S_n$, can be expressed as shown below.

\begin{aligned}S_n = a_1 + a_2 + a_3 +…+a_n  &< a_1 + \int_{1}^{n} f(x) \phantom{x}dx\\&< 1 + \int_{1}^{\infty} f(x) \phantom{x}dx\end{aligned}

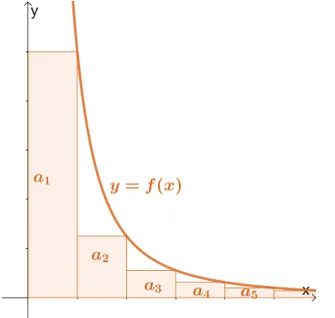
This means that the series’s convergence or divergence will depend on $\int_{1}^{\infty} f(x) \phantom{x}dx$. When $S_n$ is an increasing series, like our earlier example, the series will converge too. Hence, when $\boldsymbol{\int_{1}^{\infty} f(x) \phantom{x}dx}$ converges, the series, $\boldsymbol{\sum_{n = 1}^{\infty} a_n}$ converges too.

Now, what happens when the series satisfies the equation below?

\begin{aligned}S_n = a_1 + a_2 + a_3 +…+a_n  &< a_1 + \int_{1}^{n} f(x) \phantom{x}dx\\&< 1 + \int_{1}^{\infty} f(x) \phantom{x}dx\end{aligned}

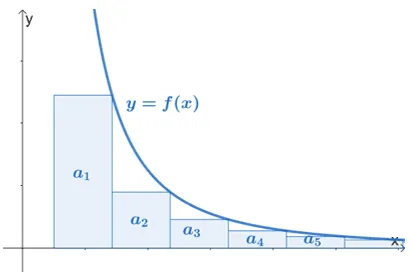
The graph above illustrates the situation and when we evaluate from $1$ to $n +1$ and as $n$ approaches infinity.  When this happens, the series will be unbounded and will cause $S_n$ to be divergent.  This means that when $\boldsymbol{\int_{1}^{\infty} f(x) \phantom{x}dx}$ diverges, the series, $\boldsymbol{\sum_{n =1}^{\infty} a_n}$, diverges as well. Let’s summarize these conditions to highlight what we need when implementing the improper integral.

When the function satisfies all three conditions, we can use the following rules to determine whether the series is convergent or divergent:

\begin{aligned} \boldsymbol{\int_{k}^{\infty} f(x) \phantom{x}dx }\textbf{ is convergent} &\Leftrightarrow  \boldsymbol{\sum_{n = k}^{\infty} a_n} \textbf{ is convergent}\end{aligned}

\begin{aligned}\boldsymbol{\int_{k}^{\infty} f(x) \phantom{x}dx }\textbf{ is divergent} &\Leftrightarrow \boldsymbol{\sum_{n = k}^{\infty} a_n} \textbf{ is divergent}\end{aligned}

Keep in mind though that $k$ is often equal to $1$ there are instances when $k \neq 1$. We’ll use these conditions to test if a given series is convergent or not. In the next section, we’ll understand how to implement the integral test on different types of series.

How to use the integral test?             

Here are some pointers that’ll help you in using the integral test to check a series’ convergence or divergence. Keep this guideline in mind when working on the sample problems we’ve prepared:

• Express $a_n$ as a function of $f(x)$.
• Check if the function satisfies the three conditions: it is continuous, decreasing, and equivalent to $f(n) = a_n$ throughout the appropriate interval.
• Set up the improper integral, $\int_{n = k}^{\infty} f(x) \phantom{x}dx$, where $k$ represents the initial index of the series.
• Evaluate the improper integral and see if it converges or diverges.
• Use the result from the previous step to determine whether the series is convergent or divergent.

Why don’t we confirm the convergence of $\sum_{n =1}^{\infty} \left(\dfrac{1}{e}\right)^n$ using the integral test?

\begin{aligned}\sum_{n =1}^{\infty} \left(\dfrac{1}{e}\right)^n &=\dfrac{1}{e} + \left(\dfrac{1}{e}\right)^2 +\left(\dfrac{1}{e}\right)^3 + \left(\dfrac{1}{e}\right)^4+ …  \end{aligned}

We let $f(x) = \left(\dfrac{1}{e}\right)^x$. The larger the exponent or the value of $x$, the smaller the value of $\left(\dfrac{1}{e}\right)^x$, so the function is continuous and decreasing. Since the series starts when $n =1$, we set up the improper integral with $k =1$. Hence, we have the following:

\begin{aligned}\int_{1}^{\infty} f(x) \phantom{x} dx &= \int_{1}^{\infty} \left(\dfrac{1}{e}\right)^x \phantom{x} dx \\&= \lim_{a \rightarrow \infty} \int_{1}^{a} \left(\dfrac{1}{e}\right)^x \phantom{x} dx\end{aligned}

Apply appropriate integral techniques to evaluate the resulting expression.

\begin{aligned}\lim_{a \rightarrow \infty} \int_{1}^{a} \left(\dfrac{1}{e}\right)^x \phantom{x} dx &= \lim_{a \rightarrow \infty} \int_{1}^{a} e^{-x} \phantom{x} dx \\&= \lim_{a \rightarrow \infty} [-e^{-x}]_1^a\\&= \lim_{a \rightarrow \infty} [(-e^{-a}) – (-e^{-1})]\\&= \lim_{a \rightarrow \infty} \left[ \dfrac{1}{e} – \dfrac{1}{e^a}\right ]\\&= \dfrac{1}{e} – 0\\&= \dfrac{1}{e}\\&\Rightarrow \textbf{converges} \end{aligned}

From this, we can see that the improper integral, $\boldsymbol{\int_{1}^{\infty} \left(\dfrac{1}{e}\right)^x \phantom{x}dx}$ converges, through the integral test, we can conclude that $\boldsymbol{\sum_{n =1}^{\infty} \left(\dfrac{1}{e}\right)^n}$ is also convergent.

Ready to work on more problems involving the integral test? Don’t worry, we’ve prepared a whole lot for you. Before diving right in, review your notes and keep your integral formulas ready as well!

Example 1

Using the integral test, confirm whether the series, $\sum_{n = 1}^{\infty} \dfrac{1}{\sqrt{n}}$, is convergent or divergent.

Solution

We’re now working with the series, $\sum_{n = 1}^{\infty} \dfrac{1}{\sqrt{n}}$.

\begin{aligned} \sum_{n = 1}^{\infty} \dfrac{1}{\sqrt{n}} = \dfrac{1}{\sqrt{1}} + \dfrac{1}{\sqrt{2}} + \dfrac{1}{\sqrt{3}} + \dfrac{1}{\sqrt{4}} + …\end{aligned}

Let’s check first if we can apply the integral test by checking the three conditions required:

• Within the interval of $[1, \infty)$, we all terms, $a_n$ can be expressed as $f(n)$, where $f(x) = \dfrac{1}{\sqrt{x}}$.
• The function, $f(x) = \dfrac{1}{\sqrt{x}}$, is continuous throughout the interval.
• The larger the value of $n$, the smaller the value of $f(x)$. For example, $\dfrac{1}{\sqrt{16}} < \dfrac{1}{\sqrt{9}}$.

We can also show mathematically that $f(x)$ is decreasing by taking its derivative.  Find the critical points of $f(x)$ then assign test values to see if $f^{\prime}(x)$ is negative or positive. When $f^{\prime}(x) < 0$, the function is decreasing.

\begin{aligned}f^{\prime}(x) &= \dfrac{d}{dx} \dfrac{1}{\sqrt{x}}\\&= -\dfrac{1}{2} x^{-\frac{1}{2} – 1}\\&= -\dfrac{1}{2}x^{-\frac{3}{2}}\\&= -\dfrac{1}{2x^{\frac{3}{2}}}\\&< 0 ,\phantom{x}x \in [1, \infty)\\& \Rightarrow \boldsymbol{f^{\prime}(x)}\textbf{ is decreasing}\end{aligned}

Since $f(x)$ satisfies all three conditions, we can now set up the improper integral, $\int_{1}^{\infty} f(x) \phantom{x}dx$ and evaluate that instead to determine whether our series is convergent or divergent.
\begin{aligned}\int_{1}^{\infty} \dfrac{1}{\sqrt{x}} \phantom{x} dx &= \lim_{a \rightarrow \infty} \int_{1}^{a} \dfrac{1}{\sqrt{x}} \phantom{x} dx \\&= \lim_{a \rightarrow \infty} \int_{1}^{a} (x)^{-\frac{1}{2}}\phantom{x} dx\\&= \lim_{a \rightarrow \infty} \int_{1}^{a} \left[\dfrac{x^{-\frac{1}{2}+1}}{-1/2 + 1} \right ]_1^a \\&= \lim_{a \rightarrow \infty} [2\sqrt{x}]_1^a \\&= \lim_{a \rightarrow \infty} (2\sqrt{a} – 2)\\&= \infty\\&\Rightarrow \textbf{diverges} \end{aligned}

Since $\int_{1}^{\infty} \dfrac{1}{\sqrt{x}} \phantom{x} dx$ is divergent, through the integral test, we can also conclude that the series, $\sum_{n = 1}^{\infty} \dfrac{1}{\sqrt{n}}$ is divergent as well.

Example 2

Using the integral test, confirm whether the series, $\sum_{n = 1}^{\infty} \dfrac{1}{n^4 }$, is convergent or divergent.

Solution

Let’s see if we can use the integral test to check if our given series is convergent or not.

\begin{aligned} \sum_{n = 1}^{\infty} \dfrac{1}{n^4 } = \dfrac{1}{1^4} + \dfrac{1}{2^4} +\dfrac{1}{3^4} +\dfrac{1}{4^4} + … \end{aligned}

Breaking down our assessment of the three conditions, we have the following:

• From $n =1$ to $n = \infty$, we can express each $n$th term by evaluating $f(n)$. This means that we can assign $f(x) = \dfrac{1}{x^4}$.
• The only time that $f(x) = \dfrac{1}{x^4}$ is not continuous occurs when $x = 0$, so we can confirm that the function is continuous within the interval, $[1, \infty)$.
• For positive integers, as $x$ increases the value of $\dfrac{1}{x^4}$ decreases. This means that $f(x)$ is indeed decreasing.

\begin{aligned}f^{\prime}(x) &= \dfrac{d}{dx} \dfrac{1}{x^4}\\&= \dfrac{d}{dx} x^{-4}\\&= -4x^{-4 -1}\\&= -\dfrac{1}{4x^{5}}\\&< 0 ,\phantom{x}x \in [1, \infty)\\& \Rightarrow \boldsymbol{f^{\prime}(x)}\textbf{ is decreasing}\end{aligned}

We have now confirmed that we can apply the integral test to determine whether the series is convergent or divergent. Now, let’s set up the improper integral, $\int_{1}^{\infty} f(x) \phantom{x}dx$, and evaluate the resulting expression to check the series for convergence.

\begin{aligned}\int_{1}^{\infty} \dfrac{1}{x^4} \phantom{x} dx &= \lim_{a \rightarrow \infty} \int_{1}^{a} \dfrac{1}{x^4} \phantom{x} dx \\&=\lim_{a \rightarrow \infty} \int_{1}^{a} x^{-4} \phantom{x} dx\\ &=\lim_{a \rightarrow \infty} \left[\dfrac{x^{-4 + 1}}{-4 + 1} \right ]_1^a \\&= \lim_{a \rightarrow \infty} \left[\dfrac{x^{-3}}{-3} \right ]_1^a\\&= \lim_{a \rightarrow \infty} \left[-\dfrac{1}{3a^3}  – \left(-\dfrac{1}{3(1)^3} \right )\right ]\\&= \lim_{a \rightarrow \infty} \left(-\dfrac{1}{3a^3} + \dfrac{1}{3} \right )\\&= 0 + \dfrac{1}{3}\\&= \dfrac{1}{3}\\&\Rightarrow \textbf{converges} \end{aligned}

We’ve shown that the improper integral, $\int_{1}^{\infty} \dfrac{1}{x^4} \phantom{x} dx$, converges to $\dfrac{1}{3}$. Through the integral test, we can also conclude that the series, $\sum_{n = 1}^{\infty} \dfrac{1}{n^4 }$, is also convergent.

Example 3

Using the integral test, confirm whether the series, $\sum_{n = 2}^{\infty} \dfrac{1}{n \ln n }$, is convergent or divergent.

Solution

The values within the interval, $[2, \infty)$, will always return a positive value for $\dfrac{1}{n\ln n }$. Why don’t we go ahead and confirm if we can use the integral test for this series:

• For all values of $n$ within the interval, $[2, \infty)$, we can assign $f(x) = \dfrac{1}{x \ln x}$ and we can see that $a_n$ will always be $f(n)$.
• There are no restrictions for $f(x) = \dfrac{1}{x \ln x}$ for the interval, $[2, \infty)$, so our function is continuous.
• We can also show that as $x$ becomes larger, the function’s value decreases, so the function is decreasing.

\begin{aligned}f^{\prime}(x) &= \dfrac{d}{dx} \dfrac{1}{x \ln x}\\&= \dfrac{d}{dx} (x \ln x)^{-1}\\&= -(x \ln x)^{-2} \cdot \left[x \cdot \dfrac{1}{x} + \ln x \cdot 1\right]\\&= -\dfrac{1}{(x \ln x)^2} \cdot (1+ \ln x)\\&= -\dfrac{1+ \ln x}{(x \ln x)^2}\\&< 0 ,\phantom{x}x \in [2, \infty)\\& \Rightarrow \boldsymbol{f^{\prime}(x)}\textbf{ is decreasing}\end{aligned}

Now that we’ve checked all three conditions, we can now move on to the next part of the process: set up the improper integral, $\int_{2}^{\infty} f(x) \phantom{x}dx$. Yes, the lower limit has to change when the index changes.

\begin{aligned}\int_{2}^{\infty} \dfrac{1}{x \ln x} \phantom{x} dx \end{aligned}

Evaluate the resulting expression to see if the improper integral is convergent or divergent.

 \begin{aligned}\int_{2}^{\infty} \dfrac{1}{x \ln x} \phantom{x} dx &= \lim_{a \rightarrow \infty} \int_{2}^{a} \dfrac{1}{x \ln x} \phantom{x} dx \\&=\lim_{a \rightarrow \infty} \int_{2}^{a} \dfrac{1}{x \ln x} \phantom{x} dx \end{aligned}

Let’s focus on integrating $f(x) = \dfrac{1}{x \ln x}$ first using the substation method then we’ll go back to our simplifying $\lim_{a \rightarrow \infty} \int_{2}^{a} \dfrac{1}{x \ln x} \phantom{x} dx$.

\begin{aligned}u &= \ln x\\du &= \dfrac{1}{x} \phantom{x}dx\\x \phantom{x}du &= dx\\\\\int \dfrac{1}{x \ln x} \phantom{x} dx &= \int \dfrac{1}{x \cdot u} \cdot x \phantom{x}du\\&= \int \dfrac{1}{u} \phantom{x}du\\&= \ln |u| + C\\&= \ln|\ln x| + C \end{aligned}

Substitute this expression for $\int \dfrac{1}{x \ln x} \phantom{x}dx$ back into our improper integral expression.

\begin{aligned}\int_{2}^{\infty} \dfrac{1}{x \ln x} \phantom{x} dx &= \lim_{a \rightarrow \infty} \int_{2}^{a} \dfrac{1}{x \ln x} \phantom{x} dx \\&=\lim_{a \rightarrow \infty} \int_{2}^{a} \dfrac{1}{x \ln x} \phantom{x} dx\\&= \lim_{a \rightarrow \infty} \left[\ln |\ln x| \right ]_2^a\\&= \lim_{a \rightarrow \infty} (\ln |\ln a| – \ln |\ln 2|)\\&= \infty \\&\Rightarrow \textbf{diverges} \end{aligned}

From this, we can see that the improper integral, $\int_{2}^{\infty} \dfrac{1}{x \ln x} \phantom{x} dx$, is divergent. Through the integral test, we can also conclude that the series, $\sum_{n = 2}^{\infty} \dfrac{1}{n\ln n }$, is divergent.

Example 4

Using the integral test, confirm whether the series, $\sum_{n = 1}^{\infty} \dfrac{1 + \sin n }{n^2 }$, is convergent or divergent.

Solution

As always, let’s make sure that we can use the integral test to check for the series:

• For the interval, $[1, \infty)$, we can the equation $a_n = f(n)$ will always be true.
• The denominator will always be positive so regardless of the values we enter, the function, $f(x) = \dfrac{1 + \sin x }{x^2 }$, will always be continuous.
• Sine functions are oscillating, so the function will be decreasing or increasing depending on the period.

This means that $f(x)$ is not decreasing throughout the interval, $[1, \infty)$. For this series, the integral test can’t be applied. Instead, we can use the comparison test to confirm that the series is convergent.

This example shows that it’s important for us to check the three conditions before applying the integral test. This will save us time form integrating the improper integral and we can then move on to using another converge test. Head over to this link if you want a quick refresher of the different converges tests.

Example 5

Using the integral test, confirm whether the series, $\sum_{n = 0}^{\infty} ne^{-n^2}$, is convergent or divergent.

Solution

For this series, we can use $f(x) = xe^{-x^2}$. All the values within the interval, $[0, \infty)$, will satisfy the equation:  $a_n = f(n)$. Why don’t we proceed in checking that the series meets all three conditions?

• Since $e^{-x^2}$ will always be positive, the function, $f(x) = xe^{-x^2}$ will be $0$ or positive as well.
• In addition, the function will be continuous throughout the interval, $[0, \infty)$.
• We can also show that $f(x)$ is decreasing by observing $f^{\prime}(x)$’s expressions.

\begin{aligned}f^{\prime}(x) &= \dfrac{d}{dx} xe^{-x^2}\\&= x(-2xe^{-x^2}) + 1(xe^{-x^2})\\&= xe^{-x^2}(1 – 2x)\\&> 0 ,\phantom{x}x \in \left[0, \dfrac{1}{\sqrt{2}}\right]\\&< 0 ,\phantom{x}x \in \left[\dfrac{1}{\sqrt{2}}, \infty\right)\\&\Rightarrow \boldsymbol{f^{\prime}(x)}\textbf{ is increasing},\phantom{x}x \in \left[0, \dfrac{1}{\sqrt{2}}\right]\\& \Rightarrow \boldsymbol{f^{\prime}(x)}\textbf{ is decreasing},\phantom{x}x \in \left[\dfrac{1}{\sqrt{2}}, \infty\right)\end{aligned}

From this, we can see that $f(x)$ is decreasing within the interval $\left[\dfrac{1}{\sqrt{2}} \right)$. Does this mean we can no longer use the integral test? Well, we still can and that’s by  observing the nature of $\sum_{n =0}^{1/\sqrt{2}} ne^{-n^2}$ and $\sum_{n = 1/\sqrt{2}}^{\infty} ne^{-n^2}$. The first series is convergent, so we can instead focus on $\sum_{n = 1/\sqrt{2}}^{\infty} ne^{-n^2}$.

Let’s now work on the improper integral, $\int_{1/\sqrt{2}}^{\infty} f(x) \phantom{x}dx$.

\begin{aligned}\int_{1/\sqrt{2}}^{\infty} xe^{-x^2} \phantom{x} dx &= \lim_{a \rightarrow \infty} \int_{1/\sqrt{2}}^{a} xe^{-x^2} \phantom{x} dx \end{aligned}

Focus on the indefinite integral first and apply the substitution method.

\begin{aligned} u& = -x^2 \\du &= -2x \phantom{x}dx\\-\dfrac{1}{2x}\phantom{x}du &= dx\\ \int xe^{-x^2} \phantom{x}dx &= \int xe^{u} \cdot -\dfrac{1}{2x}\phantom{x}du\\&= -\dfrac{1}{2} \int e^u\phantom{x}du\\&= -\dfrac{1}{2}e^u \\&= -\dfrac{1}{2}e^{-x^2}\end{aligned}

Use this expression to simplify our improper integral’s expression.

\begin{aligned}\lim_{a \rightarrow \infty} \int_{1/\sqrt{2}}^{a} xe^{-x^2} \phantom{x} dx &=\lim_{a \rightarrow \infty} \left[-\dfrac{1}{2}e^{-x^2} \right ] _{1/\sqrt{2}}^a\\&= \lim_{a \rightarrow \infty} \left(-\dfrac{1}{2}e^{-a^2} + \dfrac{1}{2}e^{-\frac{1}{2}} \right )\\&= \lim_{a \rightarrow \infty} \left(-\dfrac{1}{2e^{a^2}} + \dfrac{1}{2}e^{-\frac{1}{2}} \right )\\&= 0 +  \dfrac{1}{2}e^{-\frac{1}{2}}\\&\Rightarrow \textbf{converges} \end{aligned}

Since the improper integral, $\int_{1/\sqrt{2}}^{\infty} xe^{-x^2} \phantom{x} dx$, is convergent, through the integral test,  can confirm that $\sum_{n = 1/\sqrt{2}}^{\infty} ne^{-n^2}$ is also convergent.

\begin{aligned} \sum_{n =0}^{\infty} ne^{-n^2} &= \underbrace{\sum_{n =0}^{1/\sqrt{2}} ne^{-n^2}}_{\textbf{convergent}} + \underbrace{\sum_{n =1/\sqrt{2}}^{\infty} ne^{-n^2}}_{\textbf{convergent}}\\ &\therefore \sum_{n =0}^{\infty} ne^{-n^2} \textbf{ is convergent}\end{aligned}

Now, when two series are convergent, their sum will also be convergent. This means that the series, $\sum_{n = 0}^{\infty} ne^{-n^2}$, is also convergent.

We can shorten this solution by evaluating the improper integral from $[0, \infty)$ since a significant portion of the interval is decreasing. Keep in mind that we can only do this when only an insignificant portion of the interval is increasing. This is also why we can’t do this for the previous problem – the function was periodically increasing and decreasing.

Practice Questions

1. Using the integral test, confirm whether the series, $\sum_{n = 1}^{\infty} \dfrac{1}{\sqrt{2n -1}}$, is convergent or divergent.
2. Using the integral test, confirm whether the series, $\sum_{n = 1}^{\infty} \dfrac{1}{n^3}$, is convergent or divergent.
3. Using the integral test, confirm whether the series, $\sum_{n = 1}^{\infty} \dfrac{n}{n^2 + 1}$, is convergent or divergent.
4. Using the integral test, confirm whether the series, $\sum_{n = 2}^{\infty} \dfrac{1}{n(\ln n)^2}$, is convergent or divergent.
5. Using the integral test, confirm whether the series, $\sum_{n = 1}^{\infty} \dfrac{3n^3}{n^4 + 1}$, is convergent or divergent.
6. Using the integral test, confirm whether the series, $\sum_{n = 1}^{\infty} \dfrac{(n+ 2)^2 – n^2}{n^3}$, is convergent or divergent.
7. Using the integral test, confirm whether the series, $\sum_{n = 1}^{\infty} \dfrac{(n + \ln n)^2}{n^3 + n \ln n}$, is convergent or divergent.
8. Using the integral test, confirm whether the series, $\sum_{n = 1}^{\infty} \dfrac{3 + 2\sin (n^2)}{n^2}$, is convergent or divergent.

Answer Key

1. $\sum_{n = 1}^{\infty} \dfrac{1}{\sqrt{2n -1}}$ is divergent.
2. $\sum_{n = 1}^{\infty} \dfrac{1}{n^3}$ is convergent.
3. $\sum_{n = 1}^{\infty} \dfrac{n}{n^2 + 1}$ is divergent.
4. $\sum_{n = 2}^{\infty} \dfrac{1}{n(\ln n)^2}$ is convergent.
5. $\sum_{n = 1}^{\infty} \dfrac{3n^3}{n^4 + 1}$ is divergent.
6. $\sum_{n = 1}^{\infty} \dfrac{(n+ 2)^2 – n^2}{n^3}$ is convergent.
7. $\sum_{n = 1}^{\infty} \dfrac{(n + \ln n)^2}{n^3 + n \ln n}$ is divergent.
8. $\sum_{n = 1}^{\infty} \dfrac{3 + 2\sin (n^2)}{n^2}$ is divergent.

Images/mathematical drawings are created with GeoGebra.