- Home
- >
- Newton’s method – Process, Approximation, and Example
Newton’s method – Process, Approximation, and Example
 Newton’s method is an important application of differential calculus. This method is also known as the Newton-Raphson method, as this is a technique developed by Sir Isaac Newton and Joseph Raphson. Some equations will be challenging to solve despite our efforts and knowledge of algebraic manipulations, and this is where approximations and algorithms like Newton’s method enter.
Newton’s method is an important application of differential calculus. This method is also known as the Newton-Raphson method, as this is a technique developed by Sir Isaac Newton and Joseph Raphson. Some equations will be challenging to solve despite our efforts and knowledge of algebraic manipulations, and this is where approximations and algorithms like Newton’s method enter.
Newton’s method (or Newton-Raphson method) is used to solve the approximate roots of a function using the function’s first derivative.
In this article, we’ll sort out the equations that will benefit from this method, and of course, our goal is to make sure that we apply this method properly to approximate the roots of a given function.
We’ll also try out some equations to compare the resulting roots derived by algebraic manipulation and Newton’s method to show you how close these values are. Let’s go ahead and begin by understanding what makes this method special!
What is Newton’s method?
Newton’s method is a technique we use to solve complex equations of the form, $f(x) = 0$, using successive approximations. This numerical method relies on the geometry of curves and the tangent line/s that pass through it. This means that knowledge of derivatives and their common rules is a prerequisite to appreciating this numerical method better.
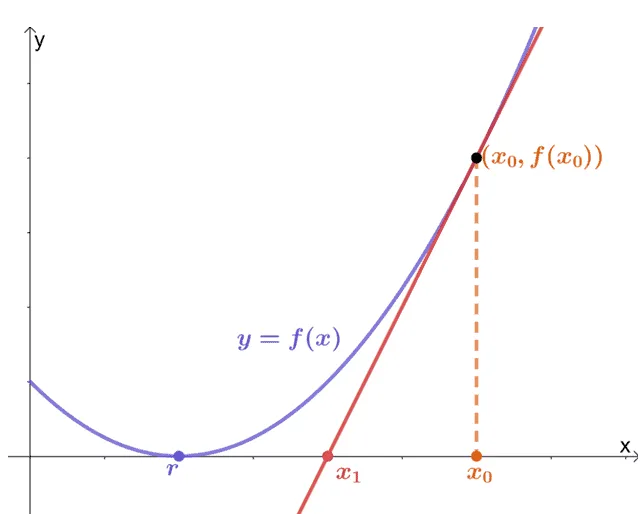
The graph shown above is a great visualization of how Newton’s method works. This numerical method relies on the tangent line (see the red line passing through $x_2$) that passes through the curve, $f(x)$. The idea is to begin with an initial value say, $x_0$, where $(x_0, f(x_0))$ is a point along the curve of $f(x)$.
We can then find a tangent line that passes through the curve and another point, $(x_1, 0)$. This point must be near $x_1$ and consequently, the actual root of $f(x)$. We stop if $f(x_1) = 0$. Otherwise, we’ll continue by finding a tangent line that passes tough $x_2$, $x_3$, and so on.
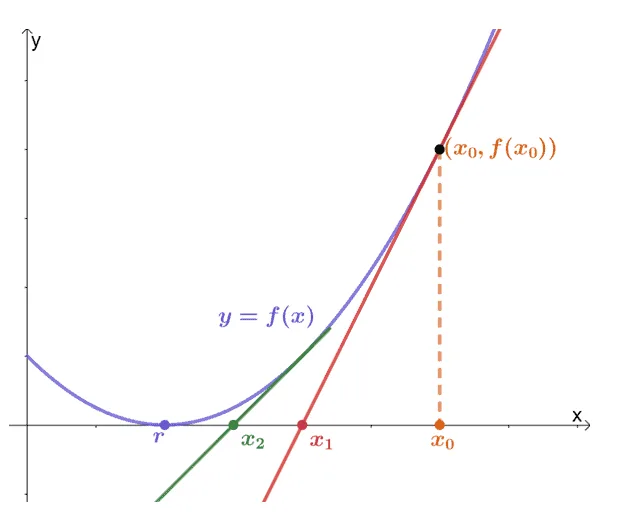
This process continues until we have $f(x_{n -1}) = 0$ or approximately close to $0$. This method will be a great help, especially when it’s difficult to find the root of $f(x)$ using traditional methods.
Traditional Method | Newton’s Method |
|
|
We’ve constructed this table to show you when the traditional method will still work best and when Newton’s method may come in handy. In the next section, we’ll further explore the process of Newton’s method and see how we can apply this to approximate roots of a given function.
How to do Newton’s method?
We can use the Newton-Rhapson method by deriving multiple tangent lines until we reach a value that is close to $f(x) = 0$. As we have mentioned, tangent lines are crucial here and hence, we’ll be repeatedly calculating for $f’(x)$. Here’s a table you can use to find the different expressions for $f’(x)$ or $\dfrac{d}{dx}$:
Helpful Derivative Rules | |
| \begin{aligned}\dfrac{d}{dx} c = 0\end{aligned} | \begin{aligned}\dfrac{d}{dx} f(g(x))= f’(g(x)) g’(x)\end{aligned} |
| \begin{aligned}\dfrac{d}{dx} x^n = nx^{n -1}\end{aligned} | \begin{aligned}\dfrac{d}{dx} e^x = e^x \end{aligned} |
| \begin{aligned}\dfrac{d}{dx} c\cdot f(x) = c \cdot f’(x)\end{aligned} | \begin{aligned}\dfrac{d}{dx} a^x = a^x \ln a \end{aligned} |
| \begin{aligned}\dfrac{d}{dx} f(x) \pm g(x) = f’(x) \pm g’(x)\end{aligned} | \begin{aligned}\dfrac{d}{dx} \sin x = \cos x\end{aligned} |
| \begin{aligned}\dfrac{d}{dx} [f(x) \cdot g(x)] = f’(x) \cdot g(x) + g’(x) \cdot f(x)\end{aligned} | \begin{aligned}\dfrac{d}{dx} \cos x = -\sin x\end{aligned} |
| \begin{aligned}\dfrac{d}{dx} \left[\dfrac{f(x)}{g(x)}\right] =\dfrac{g(x)f’(x) – f(x) g’(x)}{[g(x)]^2}\end{aligned} | \begin{aligned}\dfrac{d}{dx} \tan x =\sec^2 x\end{aligned} |
Why don’t we go ahead and derive the Newton’s method formula so we can better understand the iteration process to approximate the roots of a function?
Understanding Newton’s method formula
Let’s say we have the initial point, $(x_0, f(x_0))$, we can use this to find the equation for the tangent line. Make sure to find the expression for $f’(x)$ and consequently, $f’(x_0)$. The equation for the tangent line can be expressed as the equation shown below.
\begin{aligned}y_{\text{tangent}} &= f(x_0) + f’(x_0)(x – x_0)\end{aligned}
We can equate this equation of the tangent line to $0$ to find the value of $x$ when $y_{\text{tangent}}$ passes through the $x$-axis.
\begin{aligned}x&= \dfrac{x_0 f’(x_0) – f(x_0)}{f’(x_0)}\\&= x_0 -\dfrac{f(x_0)}{f’(x_0)}\end{aligned}
We’ll continue to iterate this process until we reach our ideal approximations for the zero of $f(x)$:
\begin{aligned}x_{n + 1} &= \dfrac{x_n f’(x_n) – f(x_n)}{f’(x_n)}\\&= x_n – \dfrac{f(x_n)}{f’(x_n)}\end{aligned}
This is how we estimate the value of the root, $r$, using the Newton’s method. Let’s recap this process once more to make sure we apply it correctly.
- If it’s not yet given, find the expression for $f’(x)$ using the different derivative rules.
- Begin with an initial value, $x_0$ that might be close to the actual root.
- Determine the first approximate using the formula shown below.
\begin{aligned}x_1 &= x_0 – \dfrac{f(x_0)}{f’(x_0)}\end{aligned}
- Repeat the iterative process using the formula shown below until we find the root within our allowed accuracy.
\begin{aligned}x_{n+1} &= x_n – \dfrac{f(x_n)}{f’(x_n)}\end{aligned}
Example of how we apply Newton’s method
Now that we’ve discussed the iterative process of approximating the roots of a function using Newton’s method, why don’t we try to approximate the zeros of $f(x) =x^3 – x – 1$ to six decimal places and with an initial value of $x_0 = 1$?
The first thing we’ll need to do is to find the derivative of $f(x) = x^3 – x – 1$.
\begin{aligned}f(x) &= x^3 – x -1\\f'(x) &= 3(x^{3-1}) -1(x^{1-1}) – 0\\&=3x^2 -1 \end{aligned}
Now that we have $f’(x)$, we can now find the first approximation for the root of $f(x)$.
- Find the values of $f(x_0)$ and $x_0$.
- Use these values to find $x_1$ using the formula, $x_1 = x_0 – \dfrac{f(x_0)}{f’(x_0)}$.
\begin{aligned}x_0 &= 1\\f(x_0) &= (1)^3 – 1 – 1\\&= -1\\f'(x_0)&= 3(1)^2 -1\\&=2\\\\x_1 &= x_0 – \dfrac{f(x_0)}{f'(x_0)}\\&= 1 -\dfrac{-1}{2}\\&=\dfrac{3}{2}\\&= 1.5\end{aligned}
We can repeat the process until we reach two successive values that are identical up to six decimal places. We can then return that value as the approximate root for the function. To make our solution more organized, let’s tabulate our results as shown below. Keep in mind that we have the following functions:
\begin{aligned}f(x) &= x^3 – x – 1\\f’(x) &= 3x^2 – 1\end{aligned}
| \begin{aligned}\boldsymbol{n}\end{aligned} | \begin{aligned}\boldsymbol{x_n}\end{aligned} | \begin{aligned}\boldsymbol{f(x_n)}\end{aligned} | \begin{aligned}\boldsymbol{f’(x_n)}\end{aligned} | \begin{aligned}\boldsymbol{x_{n+1} = x_n – \dfrac{f(x_n)}{f’(x_n)}}\end{aligned} |
| \begin{aligned}0\end{aligned} | \begin{aligned}1\end{aligned} | \begin{aligned}-1\end{aligned} | \begin{aligned}2\end{aligned} | \begin{aligned}1.5\end{aligned} |
| \begin{aligned}1\end{aligned} | \begin{aligned}1.5\end{aligned} | \begin{aligned}0.875\end{aligned} | \begin{aligned}5.75\end{aligned} | \begin{aligned}1.347826\end{aligned} |
| \begin{aligned}2\end{aligned} | \begin{aligned}1.347826\end{aligned} | \begin{aligned}0.1006822\end{aligned} | \begin{aligned}4.4499055\end{aligned} | \begin{aligned}1.325200\end{aligned} |
| \begin{aligned}3\end{aligned} | \begin{aligned}1.325200\end{aligned} | \begin{aligned}0.0.002058\end{aligned} | \begin{aligned}4.2684683\end{aligned} | \begin{aligned}1.324718\end{aligned} |
| \begin{aligned}4\end{aligned} | \begin{aligned}1.324718\end{aligned} | \begin{aligned}0.0000009\end{aligned} | \begin{aligned}4.2646347\end{aligned} | \begin{aligned}1.324718\end{aligned} |
Here’s a tip: create a spreadsheet or use a calculator that generates a table of values to help you save time in finding the approximate values. We’ve shown you a full table for this first example, but for the ones in our exercises, we’ll simplify this table in our solution so you can also work these out by yourself.
From our result, we can see that $x_3 = 1.324718$ and $x_4 = 1.324718$. We now have two consecutive values that return identical digits for its first six decimal places, so our approximation for the root of $x^3 – x – 1$ is $x \approx 1.34718$.
If you use an equation solver, the actual root of this function to six decimal places is approximately $1.324718$ as well confirming the accuracy of our approximation through Newton’s method.
As with its components, the iterative process of Newton’s method will be easier for you once you continue to practice approximating the roots of complex functions. Practice, repeat, and you’ll find that you’ll be more confident with this numerical method!
Example 1
Find the solution to the equation, $x+ e^{2x} = 0$ using the Newton’s method with an accuracy of $4$ decimal places. Use $x_0 = -1$ as your initial value.
Solution
We’ll show you the graph of $y = x + e^{2x}$ to help you understand why $x_0 = -1$ is a good initial value for this function.
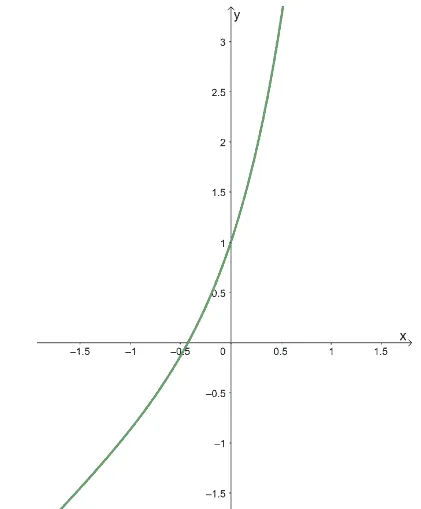
As you can see from the graph, the function $y= x+e^{2x}$ passes through the $x$-axis somewhere between $-1$ and $0$. Using $x_0 = -1$ as an initial value is actually strategic and will be a good number to work with for the first iteration.
Let’s first differentiate $x + e^{2x}$ so that we have can find $f(x_0)$ and $f’(x_0)$.
\begin{aligned}f(x)&= x+ e^{2x}\\f'(x) &= 1 + 2(e^{2x})\\&= 2e^{2x} + 1\end{aligned}
We can now find the first iteration by finding the value of $f(1)$ and $f’(1)$ then using the iteration formula for Newton’s method.
\begin{aligned}x_0 &= -1\\f(x_0) &= (-1) + e^{2(-1)}\\&=-1 + e^{-2}\\f'(x_0)&= 2(e^{-2}) + 1\\&=2e^{-2} + 1\\\\x_1 &= x_0 – \dfrac{f(x_0)}{f'(x_0)}\\&= -1 -\dfrac{-1 + e^{-2}}{2e^{-2} + 1}\\&\approx -0.3195 \end{aligned}
Notice how we didn’t estimate the values of $f(x_0)$ and $f’(x_0)$ in the first steps? This will help reduce errors since we’re only approximating at the last step. Keep this tip handy when working with similar functions. For now, we can repeat the iteration process until we have two roots that have the same digits on their first four decimal places.
This table will show you how the values of $x_{n+1}$ evolve as we add in more steps.
| \begin{aligned}\boldsymbol{n}\end{aligned} | \begin{aligned}\boldsymbol{x_n}\end{aligned} | \begin{aligned}\boldsymbol{x_{n+1} = x_n – \dfrac{f(x_n)}{f’(x_n)}}\end{aligned} |
| \begin{aligned}0\end{aligned} | \begin{aligned}-1\end{aligned} | \begin{aligned}-0.3195\end{aligned} |
| \begin{aligned}1\end{aligned} | \begin{aligned}-0.3195\end{aligned} | \begin{aligned}-0.4208\end{aligned} |
| \begin{aligned}2\end{aligned} | \begin{aligned}-0.4208\end{aligned} | \begin{aligned}-0.4263\end{aligned} |
| \begin{aligned}3\end{aligned} | \begin{aligned}-0.4263\end{aligned} | \begin{aligned}-0.4263\end{aligned} |
Once we have two consecutive values that meet out conditions, we can now stop and return the $x_2= x_3 = -0.4263$ as our approximated solution for the equation, $x+ e^{2x} = 0$, using Newton’s method.
Example 2
Find the solution to the equation, $\sin x = x^2$ using Newton’s method with an accuracy of $6$ decimal places. Use $x_0 = 1$ as your initial value.
Solution
First, let’s rewrite the equation so that we only have $0$ on the right-hand side of the equation.
\begin{aligned}\sin x &= x^2\\\sin x- x^2 &=0\end{aligned}
This means that we have to estimate the root of $f(x) = \sin x – x^2$. We can use the derivative rules (feel free to scroll up to find the table again if you need some refresher) to find the expression for $f’(x)$.
\begin{aligned}f(x) &=\sin x- x^2\\f'(x) &= \cos x – 2(x^{2-1})\\&= \cos x – 2x \end{aligned}
With this, let’s first observe how our first iteration process would look like. As with our previous example, whenever possible, let’s try approximate values only at the last step.
\begin{aligned}x_0 &= 1\\f(x_0) &= \sin (1) – (1)^2\\&=\sin 1 – 1\\f'(x_0)&= \cos (1) – 2(1)\\&=\cos 1 -2\\\\x_1 &= x_0 – \dfrac{f(x_0)}{f'(x_0)}\\&= 1 -\dfrac{\sin 1 – 1}{\cos 1 -2}\\&\approx 0.891396\end{aligned}
We’ll apply the same process to iterate the roots until we end up with two consecutive numbers that shared the same digits for its first six decimal places. We’ll show you one more calculation and the rest will be up to you – don’t worry, we’ll still summarize the essential values.
\begin{aligned}x_1 &= 0.891396\\f(x_1) &= \sin (0.891396) – (0.891396)^2\\f'(x_1)&= \cos (0.891396) – 2(0.891396)\\\\x_2 &= x_1 – \dfrac{f(x_1)}{f'(x_1)}\\&= 0.891396 -\dfrac{\sin 0.891396 – 0.891396^2}{\cos 0.891396 -2(0.891396)}\\&\approx 0.876985\end{aligned}
Make sure that the roots are in radians, so you calculator or graphing utility is in radians as well. Repeat this process until we find two consecutive identical values. Here’s a summary of the approximations after iterating the process for four steps:
| \begin{aligned}\boldsymbol{n}\end{aligned} | \begin{aligned}\boldsymbol{x_n}\end{aligned} | \begin{aligned}\boldsymbol{x_{n+1} = x_n – \dfrac{f(x_n)}{f’(x_n)}}\end{aligned} |
| \begin{aligned}0\end{aligned} | \begin{aligned}1\end{aligned} | \begin{aligned}0.891396\end{aligned} |
| \begin{aligned}1\end{aligned} | \begin{aligned}0.891396\end{aligned} | \begin{aligned}0.876985\end{aligned} |
| \begin{aligned}2\end{aligned} | \begin{aligned}0.876985\end{aligned} | \begin{aligned}0.876726\end{aligned} |
| \begin{aligned}3\end{aligned} | \begin{aligned}0.876726\end{aligned} | \begin{aligned}0.876726\end{aligned} |
We can see that we’ve successfully returned two consecutive values identical for the first six decimal places. This means that through Newton’s method, the equation’s solution, $\sin x = x^2$, is approximately $0.876726$.
This is a great approximation since the value returned by online equation solvers, and graphing utilities will be $x \approx 0.876726$ as well.
Example 3
Estimate the fifth root of $100$ to eight decimal places using the Newton-Raphson method.
Solution
Let’s say we have $x = \sqrt[5]{100}$, this represents the fifth root of $100$. We can rewrite this equation as shown below:
\begin{aligned}x &= \sqrt[5]{100}\\(x)^5 &= (\sqrt[5]{100})^5 \\x^5 &= 100\\x^5 – 100&= 0\end{aligned}
For us to estimate the value of $\sqrt[5]{100}$, we simply find the solution of the equation, $ x^5 – 100 =0$. If you’ve noticed, the initial value has not yet been given, so we let’s graph $f(x) = x^5 -100$ first to have an idea on where the root lies.
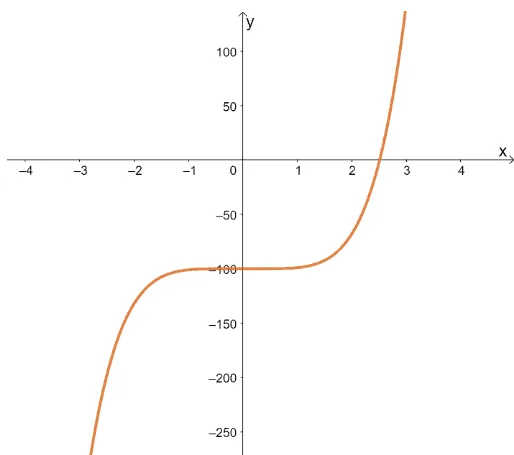
From this, we can see that the root we’re looking for lies within $[2, 3]$, so a good initial value would be $x_0 = 3$. That way, the values get closer to the actual root as we add more steps in the iteration process.
Let’s begin by finding the derivative of $f(x) = x^5 -100$ – this is a straightforward process using the power and constant rules as shown below.
\begin{aligned}f(x) &= x^5 – 100\\f'(x)&= 5x^{5-1} – 0\\&=5x^4 \end{aligned}
We can now calculate for the first approximated root as shown below.
\begin{aligned}x_0 &= 3\\f(x_0) &= (3)^5 – 100\\&=243 – 100\\&= 143\\f'(x_0)&= 5(3)^4\\&=405\\\\x_1 &= x_0 – \dfrac{f(x_0)}{f'(x_0)}\\&= 3 -\dfrac{143}{405}\\&=\dfrac{1072}{405}\\&\approx 2.64691358\end{aligned}
We can then repeat the same process until we end up with two identical consecutive values (by identical, we meant that they share the same digits for the first eight decimal places).
| \begin{aligned}\boldsymbol{n}\end{aligned} | \begin{aligned}\boldsymbol{x_n}\end{aligned} | \begin{aligned}\boldsymbol{x_{n+1} = x_n – \dfrac{f(x_n)}{f’(x_n)}}\end{aligned} |
| \begin{aligned}0\end{aligned} | \begin{aligned}3\end{aligned} | \begin{aligned}2.64691358\end{aligned} |
| \begin{aligned}1\end{aligned} | \begin{aligned}2.64691358 \end{aligned} | \begin{aligned}2.52497770\end{aligned} |
| \begin{aligned}2\end{aligned} | \begin{aligned}2.52497770\end{aligned} | \begin{aligned}2.51202148 \end{aligned} |
| \begin{aligned}3\end{aligned} | \begin{aligned}2.51202148 \end{aligned} | \begin{aligned}2.51188645\end{aligned} |
| \begin{aligned}4\end{aligned} | \begin{aligned}2.51188645 \end{aligned} | \begin{aligned}2.51188643\end{aligned} |
| \begin{aligned}5\end{aligned} | \begin{aligned}2.51188643\end{aligned} | \begin{aligned}2.51188643\end{aligned} |
By the fifth and sixth iteration, we’ll end up with $2.51188643$. This means that through Newton’s method, it is also possible for us to estimate $\sqrt[5]{100}$ to eight decimal places. In fact, we have $x \approx 2.51188643$ through Newton’s method.
What’s amazing about this is that when you actually input $\sqrt[5]{100}$ in your calculator, you’ll end up with the same approximated value to the nearest eight decimal places ($\sqrt[5]{100} \approx 2.511886432$).
Example 4
Determine one approximate solution for the equation,$\sin (e^x) = -1$. Estimate the root to the nearest five decimal places and ensure that the solution is within the interval, $[0, \pi]$.
Solution
We’ll rearrange the equation, $\sin(e^x) = -1$, so we end up with all the terms on the left-hand side of the equation and $0$ on the right-hand side of the equation.
\begin{aligned}\sin(e^x) &= -1\\\sin(e^x) +1 &= 0\end{aligned}
The function, $y = \sin(e^x) + 1$, will pass through multiple roots when between $0$ and $\pi$. We need one solution to end up with a different initial value than the one used in this solution.
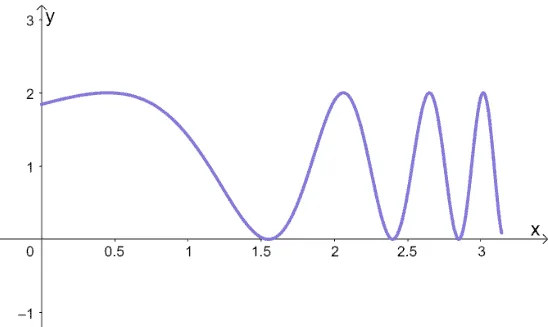
For our discussion, we’ll use $x_0 = 2$ as our initial value. Now that we’ve established a good initial value, let’s find the derivative of $f(x) = \sin(e^x) + 1$. Be careful with differentiating this equation and make sure to account for the chain rule.
\begin{aligned}f(x) &= \sin(e^x) + 1\\f'(x) &= \cos(e^x) \cdot \dfrac{d}{dx} (e^x) + 0\\&= e^x\cos(e^x)\end{aligned}
Now that we have $f’(x) = e^x \cos (e^x)$ and $x_0 = 2$, we can find the first approximated solution of the equation.
\begin{aligned}x_0 &= 2\\f(x_0) &= \sin(e^2) + 1\\&=\sin e^2 + 1\\f'(x_0)&= e^2\cos(e^2)\\&=e^2 \cos e^2\\\\x_1 &= x_0 – \dfrac{f(x_0)}{f'(x_0)}\\&= 2 -\dfrac{\sin e^2 + 1}{e^2 \cos e^2}\\&\approx 1.42834\end{aligned}
As you can see from this calculations, we always try our best to hold off approximating the roots until the very last step. Make sure to also set your calculator or graphing utility in radian mode when finding the approximated roots. We’ll show you one more detailed calculation as a guide:
\begin{aligned}x_2 &= x_1- \dfrac{f(x_1)}{f'(x_1)}\\&= 1.42834 -\dfrac{\sin e^{1.42834} + 1}{e^{1.42834} \cos e^{1.42834}}\\&\approx 1.49476\end{aligned}
Do the same for the rest of the iterations until we end up with two consecutive values with matching digits in their first decimal places. Here’s a summary of all the steps we’ll making until we reach our desired root.
| \begin{aligned}\boldsymbol{n}\end{aligned} | \begin{aligned}\boldsymbol{x_n}\end{aligned} | \begin{aligned}\boldsymbol{x_{n+1} = x_n – \dfrac{f(x_n)}{f’(x_n)}}\end{aligned} |
| \begin{aligned}0\end{aligned} | \begin{aligned}2\end{aligned} | \begin{aligned}1.42834\end{aligned} |
| \begin{aligned}1\end{aligned} | \begin{aligned}1.42834 \end{aligned} | \begin{aligned}1.49476\end{aligned} |
| \begin{aligned}2\end{aligned} | \begin{aligned}1.49476\end{aligned} | \begin{aligned}1.52342\end{aligned} |
| \begin{aligned}3\end{aligned} | \begin{aligned}1.52342 \end{aligned} | \begin{aligned}1.53700\end{aligned} |
| \begin{aligned}4\end{aligned} | \begin{aligned}1.53700\end{aligned} | \begin{aligned}1.54365\end{aligned} |
| \begin{aligned}5\end{aligned} | \begin{aligned}1.54365\end{aligned} | \begin{aligned}1.54693\end{aligned} |
| \begin{aligned}6\end{aligned} | \begin{aligned}1.54693\end{aligned} | \begin{aligned}1.54857\end{aligned} |
| \begin{aligned}7\end{aligned} | \begin{aligned}1.54857\end{aligned} | \begin{aligned}1.54938\end{aligned} |
| \begin{aligned}8\end{aligned} | \begin{aligned}1.54938\end{aligned} | \begin{aligned}1.54979 \end{aligned} |
| \begin{aligned}9\end{aligned} | \begin{aligned}1.54979 \end{aligned} | \begin{aligned}1.54999\end{aligned} |
| \begin{aligned}10\end{aligned} | \begin{aligned}1.54999\end{aligned} | \begin{aligned}1.55009\end{aligned} |
| \begin{aligned}11\end{aligned} | \begin{aligned}1.55009\end{aligned} | \begin{aligned}1.55014\end{aligned} |
| \begin{aligned}12\end{aligned} | \begin{aligned}1.55014\end{aligned} | \begin{aligned}1.55017\end{aligned} |
| \begin{aligned}13\end{aligned} | \begin{aligned}1.55017\end{aligned} | \begin{aligned}1.55018\end{aligned} |
| \begin{aligned}14\end{aligned} | \begin{aligned}1.55018\end{aligned} | \begin{aligned}1.55019\end{aligned} |
| \begin{aligned}15\end{aligned} | \begin{aligned}1.55019\end{aligned} | \begin{aligned}1.55019\end{aligned} |
This iteration took more steps than the previous examples, but at the fifteenth and sixteenth iteration, we have $x \approx 1.55019$ through the Newton’s Method. We’ve mentioned that there are other roots for this equation, so here are some initial values and the approximated roots that you might end up with instead.
| \begin{aligned}\boldsymbol{x_0}\end{aligned} | \begin{aligned}\boldsymbol{x}\end{aligned} |
| \begin{aligned}x_0 = 2.5\end{aligned} | \begin{aligned}x \approx 2.39749\end{aligned} |
| \begin{aligned}x_0 = 3\end{aligned} | \begin{aligned}x \approx 2.84948\end{aligned} |
| \begin{aligned}x_0 = 3.2\end{aligned} | \begin{aligned}x \approx 3.15963\end{aligned} |
You can try working on these three other roots as additional exercises and see if you can get the approximated roots shown above.
Practice Questions
1. Find the solution to the equation, $x^3 + 2x^2 + 1= 0$ using the Newton’s method with an accuracy of $5$ decimal places. Use $x_0 = -2$ as your initial value.
2. Find the solution to the equation, $2x+ e^{3x} = 0$ using the Newton’s method with an accuracy of $5$ decimal places. Use $x_0 = –1$ as your initial value.
3. Find the solution to the equation, $\cos x = 2x^2$ using Newton’s method with an accuracy of $6$ decimal places. Use $x_0 = 1$ as your initial value.
4. Estimate the seventh root of $32$ to eight decimal places using the Newton-Raphson method.
5.Determine one approximate solution for the equation,$\cos (e^2x) = 1$. Estimate the root to the nearest five decimal places and make sure that the solution is within the interval, $\left[0, \dfrac{\pi}{2}\right]$.
Answer Key
1. $x\approx -2.20557$
2. $x\approx -0.24195$
3. $x \approx 0.634560$
4. $\sqrt[7]{32} \approx 1.64067071$
5. $x \approx 0.91894$, $x \approx 1.26552$, or $x \approx 1.46825$
Images/mathematical drawings are created with GeoGebra.
