Oblique asymptotes – Properties, Graphs, and Examples

Graphs and functions can also have slanted or oblique asymptotes. What happens when the asymptote of a function is a (linear) function itself? This article will feature a unique element of rational functions – oblique asymptotes.

Oblique asymptotes represent the linear functions guiding the end behaviors of a rational function from both ends.

Learning about oblique asymptotes can help us predict how graphs behave at the extreme values of $x$. Since this article will focus on the oblique asymptotes found in a rational function, so we recommend checking out some important properties of rational functions:

• Learn about rational functions and their graphs here.
• Make sure to review your knowledge on horizontal and vertical.

When we also learn about graphing oblique asymptotes, we’ll also need to review our knowledge of graphing linear equations. Are you ready to further your knowledge on oblique asymptotes? Let’s begin with its definition.

What is a oblique asymptote?

Oblique asymptotes are also known as slanted asymptotes. That’s because of its slanted form representing a linear function graph, $y = mx + b$. A rational function may only contain an oblique asymptote when its numerator’s degree is exactly one degree higher than its denominator’s degree.

Oblique asymptotes are the linear functions that we can use to predict rational functions’ end behavior, as shown by our example below.

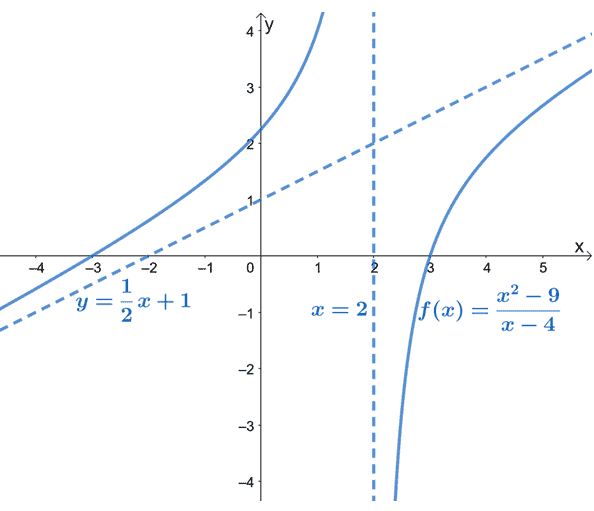
As can be seen from the graph, $f(x)$’s oblique asymptote is represented by a dashed line guiding the graph’s behavior. We can also see that $y= \dfrac{1}{2}x     +1$ is a linear function of the form, $y = mx + b$.

The slanted asymptote gives us an idea of how the curve of $f(x)$ behaves as it approaches $-\infty$ and $\infty$. The graph of $f(x)$ also confirms what we already know: that oblique asymptotes will be linear (and slanted).

Noticed how $f(x)$ has no horizontal asymptotes? That’s because a rational function may only have either a horizontal asymptote or an oblique asymptote, but never both.

How to find the oblique asymptote?

When finding a rational function’s oblique asymptote, we might need to refresh our memory on the following topics:

• Review on how we can perform long divisions on polynomials.
• We will also need to use synthetic division, so it’s best to refresh your knowledge.

Note that both methods should return the same result – we will only depend on the numerator and denominator’s forms to decide which of the two methods is best.

 Since $f(x) = \dfrac{p(x)}{q(x)}$, is a rational function with $p(x)$ having one degree higher than $q(x)$, we can find the quotient of $\dfrac{p(x)}{q(x)}$ to find the oblique asymptote.

$f(x) = \text{Quotient } + \dfrac{\text{Remainder}}{q(x)}$

When finding the oblique asymptote, we only focus on the quotient and disregard the remainder.

Oblique asymptote rules for rational functions

When finding the oblique asymptote of a rational function, we always make sure to check the degrees of the numerator and denominator to confirm if a function has an oblique asymptote. See to it that the numerator’s degree is exactly one degree higher.

Rule 1: If the numerator is a multiple of the denominator, the oblique asymptote will be the simplified form of the function.

Let’s say we have $f(x) = \dfrac{x^2 – 9}{x – 3}$, $x^2 – 9$ is equivalent to $(x -3)(x +3)$ in factored form, so the denominator is a factor of the numerator.

The simplified form $f(x)$ is $ \dfrac{\cancel{(x-3)}(x +3)}{\cancel{x -3}} = x+3$. This means that the function has an oblique asymptote at $y = x + 3$.

It’s helpful to keep this in mind since canceling out factors will be a much faster approach.

Rule 2: If the numerator is not a multiple of the denominator, use long division or synthetic division to find the quotient of the function.

Suppose we have $f(x) = \dfrac{x^2 – 6x + 9}{x – 1}$. We can see that the numerator has a higher degree (by exactly one degree), so $f(x)$ must have an oblique asymptote.

We can use synthetic division to find the quotient of $x^2 – 6x + 9$ and $x – 1$. (Make sure to review your knowledge on dividing polynomials.)

$\frac{\begin{array}{r|}1\end{array}}{\phantom{2}}\underline{\begin{array}{rrr}1&-6&9 \\&1&-5\end{array}}$

$\begin{array}{rrrr}~~&1&-5\phantom{2}&4 \end{array}$

This shows that the quotient is $x – 5$. We can also confirm this through long division as shown below.

$ \begin{array}{r}\color{blue}x – 5 \phantom{} \\x-1{\overline{\smash{\big)}\,x^2-6x+9}}\\\underline{-~\phantom{(}x^2 – x ~~~~~\downarrow}\\0-5x+9 \\ \underline{-~\phantom{(}(-5x+5)}\\ \color{red}4\phantom{x}\end{array}$

From these two methods, we can see that $f(x) = x – 5 + \dfrac{4}{x + 1}$, so focusing on the quotient, the oblique asymptote of $f(x)$ is found at $y = x – 5$.

How to graph oblique asymptote?

Once we have the equation representing the oblique asymptote, graph the linear function as a slant dashed line.

 Make sure to review your knowledge of graphing linear functions. But don’t worry, here are important reminders in graphing linear functions:

• When the equation is of the form $y = mx + b$, remember that the graph passes the $y$-intercept, $(0, b)$.
• Find another point that satisfies the equation – normally, it’s the $x$-intercept.
• Connect these two points with a dashed line to graph the oblique asymptote.

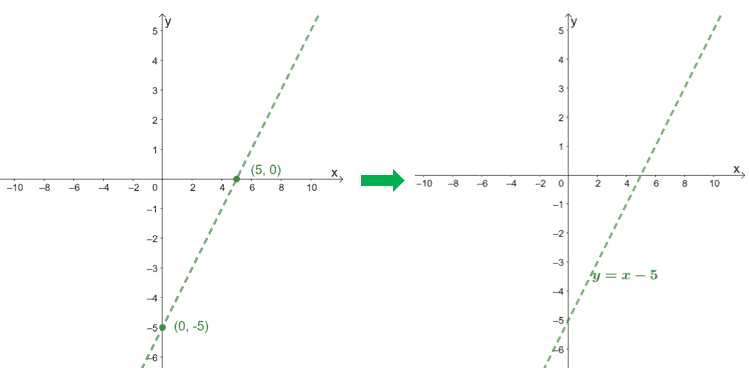
To graph the oblique asymptote of $f(x) = \dfrac{x^2 – 6x + 9}{x – 1}$, we use the intercepts of its quotient, $x – 5$.

Checking the denominator, we can see that $f(x)$ has a vertical asymptote at $x = 1$. Let’s include this as well the graph of $f(x)$ to see how the curve behaves.

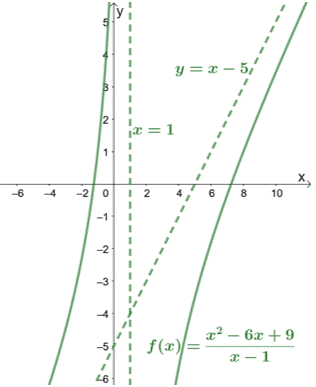
As shown from the graph, the asymptotes can also guide us in knowing how far the curves cover.

By inspecting the graph for oblique asymptotes, we can immediately conclude that the function’s numerator is one degree higher than its denominator.

Summary of oblique asymptote definition and properties

We’ve learned a lot about oblique asymptotes already, so we should summarize the important properties of oblique asymptotes before we try out more examples.

• If the function’s numerator has is exactly one degree higher than its denominator, the function has an oblique asymptote.
• The oblique asymptote has a general form of $y = mx +b$, so we expect it to return a linear function.
• Graph the linear function using the oblique asymptote’s intercepts as guides.

Don’t also forget to refresh your knowledge on the past topics we’ve mentioned in this article. When you’re ready, try out these sample problems we’ve prepared!

Example 1

Given that when the numerator is divided by the denominator of $f(x) = \dfrac{x^5 + 5x – 10x +2x – 1}{x^4 – 2}$, $f(x)$ can be written as $f(x) = x + \dfrac{-x – 1}{x^4 -2}$.

    a. What is the oblique asymptote of $f(x)$?

    b. Will $f(x)$ have any other asymptotes?

    c. Where would the oblique asymptote and $f(x)$ intersect?

Solution

Recall that oblique asymptotes are of the form, $y=mx + b$, and can be determined by finding the quotient of $f(x)$.

We have $f(x) = \boldsymbol{x} + \dfrac{-x – 1}{x^4 -2}$, so the oblique asymptote of $f(x)$ is $\boldsymbol{y = x}$.

When a function contains an oblique asymptote, $f(x)$ has no horizontal asymptotes. To find the vertical asymptote, we can equate the denominator to $0$ and solve for $x$.

$ \begin{aligned}x^4 – 2&=0\\x^4&=2\\ x&= \pm \sqrt[4]{2}\end{aligned}$

This means that aside from the oblique asymptote, $f(x)$ also has two vertical asymptotes at $x = – \sqrt[4]{2}$ and $x = \sqrt[4]{2}$.

To find the intersecting point shared by the oblique asymptote, $y = x$, and the function, we can equate $y = x$ with the $y= x + \dfrac{-x – 1}{x^4 -2}$ then solve for $x$.

$ \begin{aligned}x + \dfrac{-x – 1}{x^4 -2}&=x\\x + \dfrac{-x – 1}{x^4 -2}\color{red}{-x}&=x\color{red}{-x}\\\dfrac{-x – 1}{x^4 -2}&=0\\ -x-1&=0\\ x&=-1\end{aligned}$

We can see that the $x$-coordinate of the intersection is $-1$. To find the $y$-coordinate, substitute $x=-1$ into the oblique asymptote’s equation: $y = -1$.

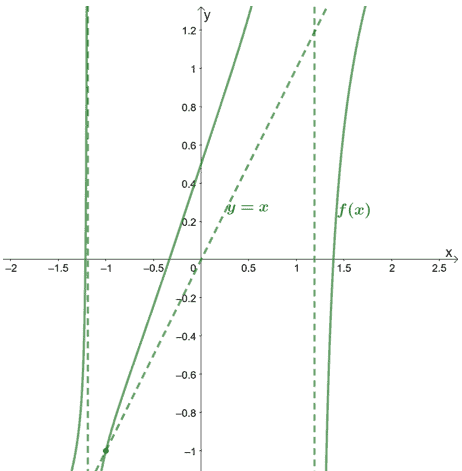
This means that $f(x)$ and its oblique asymptote intersects at $\boldsymbol{(-1,-1)}$.

Let us show you how the graph and its asymptotes would look like.

Example 2

Find the oblique asymptotes of the following functions.

    a. $f(x) = \dfrac{x^2 -25}{x – 5}$

    b. $g(x) = \dfrac{x^2 – 2x + 1}{x + 5}$

    c. $h(x) = \dfrac{x^4-3x^3+4x^2+3x-2}{x^2-3x+2}$

Solution

Always go back to the fact we can find oblique asymptotes by finding the quotient of the function’s numerator and denominator.

Using the difference of two squares, $a^2 – b^2 = (a-b)(a+b)$, $x^2-25$ can be factored as $(x – 5)(x+5)$. This means that $f(x)$ can be simplified as $\dfrac{\cancel{(x-5)}(x+5)}{\cancel{x – 5}} = x+5$.

a. This means that $f(x)$ has an oblique asymptote at $y = x+5$.

 For the second expression, since the divisor is a binomial, it’s best to use synthetic division.

$\frac{\begin{array}{r|}-5\end{array}}{\phantom{2}}\underline{\begin{array}{rrr}1&-2&1 \\&-5&35\end{array}}$

$\begin{array}{rrrr}~~&1&-7\phantom{x}&36 \end{array}$

This means that $g(x) = x – 7 +\dfrac{36}{x-5}$, so the quotient is $x – 7$.

b. Hence, the oblique asymptote of $g(x)$ is $y = x – 7$.

The third function has a trinomial on its denominator, so we can use long division to find the quotient of $ x^4-3x^3+4x^2+3x-2$ and $ x^2-3x+2$.

$ \begin{array}{r}\color{blue}x^2+2 \phantom{+ax+b} \\x^2-3x+2{\overline{\smash{\big)}\,x^4-3x^3+4x^2+3x-2}}\\\underline{-~\phantom{(}(x^4-3x^3+2x^2) ~\downarrow ~~~~ \downarrow}\\2x^2+3x-2 \\ \underline{-~\phantom{(}(2x^2-6x+4)}\\ \color{red}9x-6~~\end{array}$

From this, we can see that $h(x)$ has a quotient of $x^2 +2$. This asymptote, $y = x^2 +2$ is quadratic, so it will not form a line (a requirement for oblique or slant asymptotes).

c. This means that $h(x)$ has no oblique asymptote.

Example 3

The function, $f(x) = \dfrac{p(x)}{q(x)}$, has an oblique asymptote that passes through the points $(0, 10)$ and $(5, 0)$.

    a. What is the equation of $f(x)$’s oblique asymptote?

    b. What is the quotient of $p(x)$ and $q(x)$?

Solution

The general form of oblique asymptotes is $y=mx + b$, where $b$ is the $y$-intercept. Since $f(x)$ passes through $(0, 10)$, the equation for our oblique asymptote is $y = mx + 10$.

Find the $m$ or the slope of the line using the formula, $m = \dfrac{y_2- y_1}{x_2 – x_1}$.

$\begin{aligned}m &= \dfrac{0-10}{5 – 0}\\&=\dfrac{-10}{5}\\&=-2\end{aligned}$

Hence, the equation of the oblique asymptote is $\boldsymbol{y = -2x + 10}$.

Recall that the quotient of $\dfrac{p(x)}{q(x)}$ will return the equation for the function’s oblique asymptote.

This means that the quotient of $\boldsymbol{p(x)}$ and $\boldsymbol{q(x)}$ is equal to $\boldsymbol{-2x + 10}$.