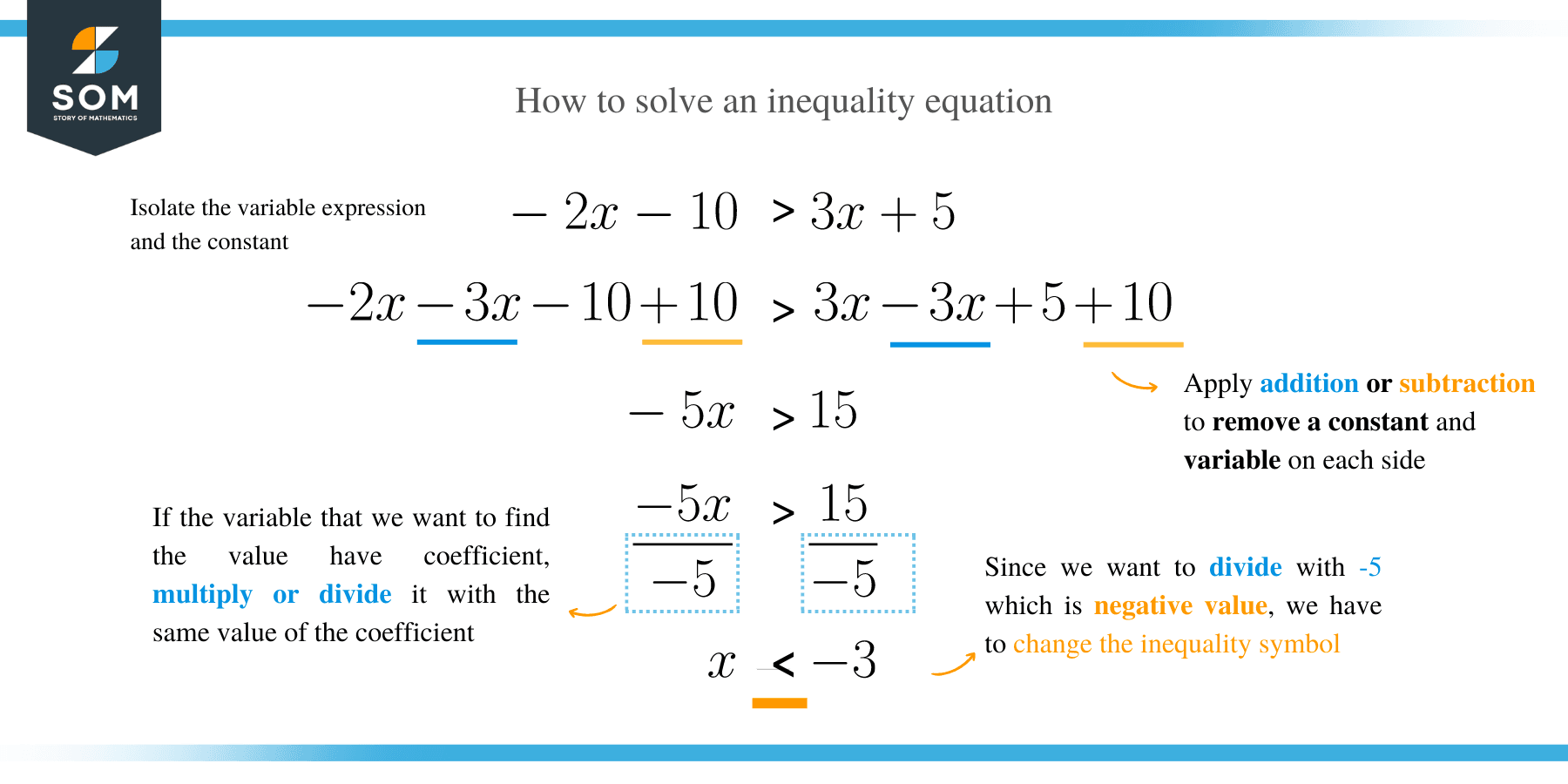Solving Single-step Inequalities – Methods & Examples

Before we can learn how to solve one-step inequalities, let’s remind ourselves of a few basic information regarding inequalities.

The word inequality means a mathematical expression in which the sides are not equal to each other. Basically, there are five inequality symbols used to represent equations of inequality.

These are:
less than (<),
greater than (>),
less than or equal (≤),
greater than or equal (≥)
and the not equal symbol (≠).

Inequalities are used to compare numbers and determine the range or ranges of values that satisfy the conditions of a given variable.

How to Solve Single-step Inequalities?

Solving a single-step inequality is a straightforward process as it sounds. Only one step is required to solve the equations completely.

The main objective of solving one-step inequality is to isolate a variable on one side of the inequality symbol and make the variable’s coefficient equal to one.

The strategy of isolating a variable entails the use of opposite operations. For instance, to move a number subtracted from the other side of the inequality, you should add.

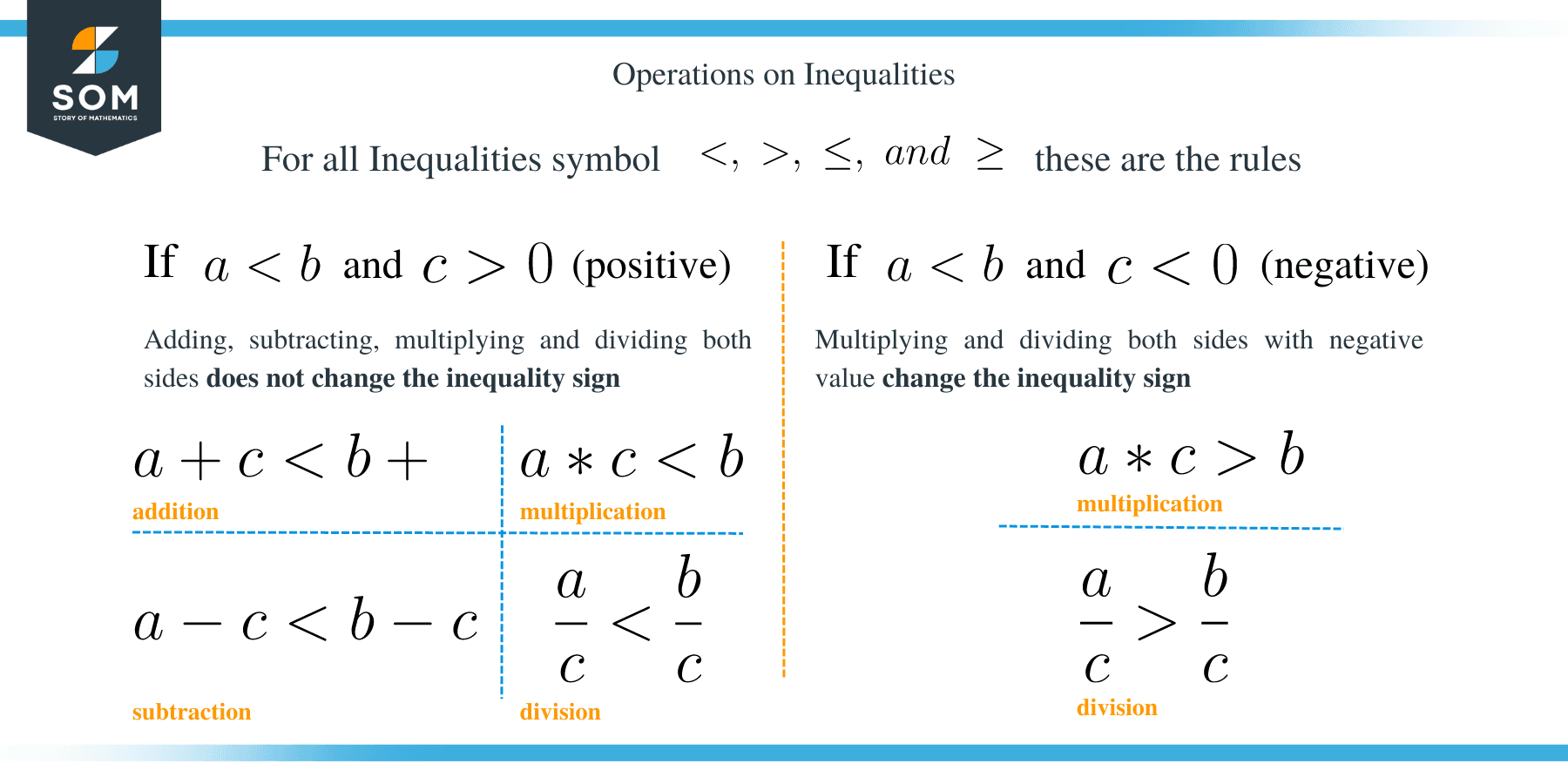
The most important step to remember when solving any linear or inequality equations to perform the same operation on both the right-hand side and left-hand side of the equation.

In other words, if you subtract or add from one side of the inequality, you must also subtract or add with the same value from the opposite side. Similarly, if you multiply or divide on one side of the equation, you must also multiply or divide with the same value on the equation’s other side.

The only exception when dividing and multiplying by a negative number in the inequality equation is that the inequality symbol reverses.

We can summarize the rules for solving one step inequalities as shown below:

• Subtracting or adding the same number from both sides of an inequality results in the inequality symbol being unchanged.
• Dividing or multiplying both sides by a positive number results in the inequality symbol being unchanged.
• Multiplying or dividing both sides by a negative number changes the inequality. This implies that, < changes to >, and vice versa.

In this article, we are going to cover five different cases of solving one-step inequalities. These cases of one-step inequalities are based on how the equations are manipulated.

The five cases include:

• Solving Single-Step Inequalities by Addition
• Solving Single-Step Inequalities by Subtraction
• One-step inequalities are solved by multiplying both sides of the equation by a number.
• One-step inequalities are solved by dividing the same number into both sides of the equation.
• One-step inequalities are solved by multiplying the reciprocal coefficient of the term with a variable to both sides of the equation.

Solving one-step inequalities by adding

Follow the steps in the examples below to understand this.

Example 1

Solve the one-step equation x – 4 > 10

Solution

Notice that the left side of the inequality symbol has a variable x subtracted by 4, whereas the left side has a positive number 10. In this case, we will keep our variable on the left side.

To isolate the variable x, we add both sides of the equation by 4, which gives;

x – 4 + 4 > 10 +4

x > 14

Example 2

Solve x – 6 > 14

Solution

x – 6 > 14

Add both sides of the equation by 6
x – 6 + 6 > 14 + 6
x > 20

Example 3

Solve the inequality –7 – x < 9

Solution

–7 – x < 9

Add 7 to both sides of the equation.
7 – x + 7 < 9 + 7
– x < 16 Multiply both sides by –1 and reverse the sign x > –16

Example 4

Solve 4 > x – 3

Solution

In this example, the variable is located on the RHS of the equation. We can isolate a variable in an equation regardless of where it is located. Therefore, let’s leave on the right side, and to do this, add 3 to both sides of the equation.

4+ 3 > x – 3 + 3

7 > x

And there, we are done!

Solving Single-Step Inequalities by Subtraction

Follow the steps in the examples below to understand this.

Example 5

Solve x + 10 < 16

Solution

x + 10 < 16

Subtract 7 from both sides of the equation.
x + 10 – 10 < 16 – 10
x < 6

Example 6

Solve the inequality 15 > 26 – y

Solution

15 > 26 – y

Subtract 26 from both sides of the equation
15 -26 > 26 – 26 -y
– 11 > -y

Multiply both sides by –1 and reverse the sign

11 < y

Example 7

Solve x + 6 > –3

Solution

Subtract both sides by 6.

x + 6 – 6 > –3 – 6

x > – 9

Example 8

Solve the one-step equation 13 < y + 8

Solution

In this case, the variable y is also located on the right side of the equation. That is okay! We will keep to the left side by subtracting both sides by 8.

13– 8 < y + 8 – 8

5 < y

Example 9

Solve for t in the following equation:

t + 18 < 21

Solution

To isolate t on the left side of the equation, we subtract both sides of the equation by 18.

t + 18 -18 < 21 – 18

t < 3

Solving one-step inequalities by multiplying both sides of the equation by a number

Follow the steps in the examples below to understand this.

Example 10

Solve for x in the following one step equation:

x/4 > 8

Solution

To eliminate a fraction, multiply both sides of the equation by the denominator of the fraction.

4(x/4) > 8 x 4

x > 32

And that is it!

Example 11

Solve the one-step equation -x/5 > 9

Solution

In this inequality, a variable x is divided by 5. Since our goal is to undo the division of the variable, therefore we multiply both sides of the inequality by

5(-x/5) > 9 x 5

-x > 45

Now multiply both sides by -1 and reverse the sign.

x < – 45

Example 11

Solve 2 > –x

Solution

You can notice that this equation is almost solved. But not quite. So, we need to eliminate a negative sign from the variable. We can do this by multiply both sides of the equation by -1 and reverse the sign.

2 * -1 > –x * -1

-2 < x

Solving one-step inequalities by dividing the same number into both sides of the equation

Follow the steps in the examples below to understand this.

Example 12

Solve for x, 2x – 4 < 0

Solution

Add 4 both sides

2x – 4 + 4 < 0 + 4

2x < 4

Divide each side by 2, we get

2x/2 < 4/2

x <4/2

So, x < 2 is the answer!

Example 13

Solve the one-step equation. 5x < 100.

Solution

In this example, a variable x is being multiplied by a number. To undo the multiplication, we will divide both sides of the equation by the variable’s coefficient. The division is normally used to cancel the effect of multiplication.

5x/5 < 100/5

x < 20

Example 14

21 < -3x

Solution

In this case, the variable is on the equation’s right, so don’t bother swapping the equation. Since the variable’s coefficient is not equal to 1, this means we need to do an opposite operation to remove 3 from -x. So, we will divide both sides by -3.

21/3<-3/3x

7 < -x Since this inequality is not simplified, we need to eliminate the variable’s negative sign. Therefore, we multiply both sides of the equation by -1 and reverse the sign. -7 > x

Example 15

Solve −2x < 4

Solution

To solve this one-step equation, we need to divide both sides by −2.

Since we’re dividing both sides of the equation by a negative number, we will reverse the inequality sign.

x > -2

Example 16
Solve the one-step inequality −2x > −8

Solution

Divide both sides of the equation by 2.

−2x/2 > −8/2

−x > − 4

Multiply both sides by -1 and reverse the inequality sign.

x < 4

Solving one-step inequality by multiplying the reciprocal of the coefficient of a variable to both sides of the equation.

Follow the steps in the examples below to understand this.

Example 17

Solve the one-step equation (4x/11) < 4

Solution

Many people are thrown off when presented with one-step inequalities containing fractions.

So, how do we solve such kinds of problems?

We can solve one-step inequalities bearing fractions by multiplying both sides of the equation by the reciprocal of the fraction. In this case, our reciprocal is 11/4.

(4x/11)11/4 < 4 * 11/4

x < 11