- Home
- >
- Parabola – Properties, Components, and Graph
Parabola – Properties, Components, and Graph
 Parabolas are the first conic that we’ll be introduced to within our Algebra classes. These conics that open upward or downward represent quadratic functions. This is also what makes parabolas special – their equations only contain one squared term.
Parabolas are the first conic that we’ll be introduced to within our Algebra classes. These conics that open upward or downward represent quadratic functions. This is also what makes parabolas special – their equations only contain one squared term.
Parabolas are the U-shaped conics that represent quadratic expressions. These are the result of a cone being sliced through diagonally by a plane.
Parabolas are used to model projectile motions and the shape of reflectors. These conics have extensive applications in physics, architecture, engineering, and more. This is why understanding the properties and components of parabolas are essential when studying conic sections.
In this article, we’ll learn about parabolas extensively, including the following:
Being familiar with the different standard forms of parabolas.
Knowing when the parabolas open vertically or horizontally.
Learn how to graph parabolas given their components or equations.
Let’s begin by understanding how parabolas are obtained and their different possible forms. We’ll eventually learn how we can apply these in real-world applications by solving some word problems.
What is a parabola?
Parabolas are the resulting conic sections when cones (or a double cone) are cut by an inclined plane at the same side of the cone, as shown by the model below.
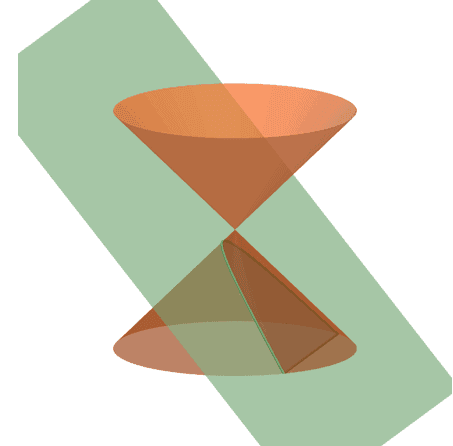
From this image, we can see that the resulting intersection will return a U-shaped section. When this happens, the conic formed is a parabola.
When cut at a particular angle, the parabola may be symmetrical along the horizontal direction or the vertical direction. Now that we can visualize how parabolas are formed, it’s time we dive into its formal definition.
This includes graphing, knowing the parabola’s different components, and identifying the parabola’s orientation immediately.
Formal parabola definition
Parabolas are curves that contain points where their distances from the focus and their distances from the directrix will always be equal. The model below can help us visualize what this definition means.
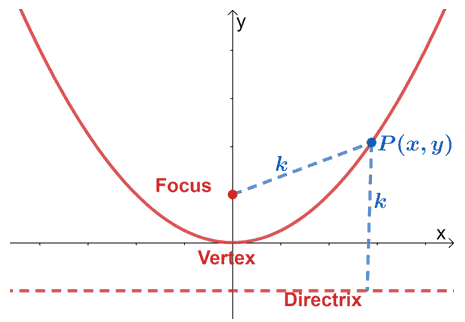
A parabola will contain three important elements: a focus, a directrix, and a vertex. This parabola that opens upward shows that all points, $P$, along the parabola’s curve will share the same distance from the focus and the directrix.
This means that the distance from the focus and $P$ and the $P$ from the directrix will be constant regardless of $P$’s position.
Keep in mind that this applies with the vertex as well – the distance between the vertex and focus will be the same as the distance between the vertex and the directrix.
How to find the equation of a parabola?
As we have mentioned in the earlier section, parabolas can either open upward, downward to the right side and the left. The equations representing these equations will also vary, so we need to learn the four standard forms representing parabolas.
Parabola formula
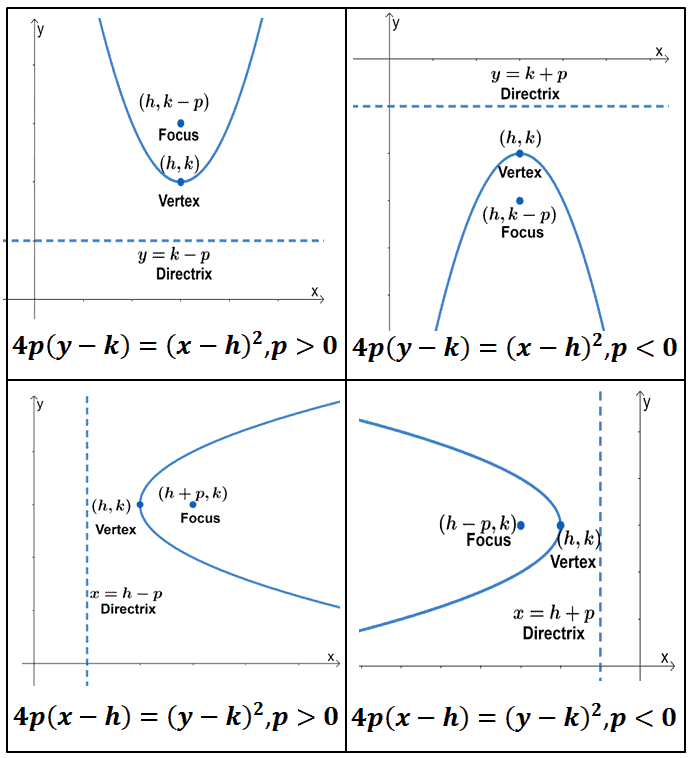
The parabolas’ standard form will vary depending on two factors: the parabola’s vertex and the orientation of the parabola.
The vertex of the parabola’s graph can either be $(0, 0)$ or $(h, k)$.
The sign of $p$ and which of the terms are squared will determine whether the graph will open upwards, downwards, to the left or right.
These options will lead to four options for the standard form of the parabola.
The below summarizes the standard forms for the parabola considering these conditions.
Center | Orientation | Sign of $\boldsymbol{p}$ | Equation |
\begin{aligned}(0, 0) \end{aligned} | Opening Upwards, Opening Downwards | \begin{aligned}p &> 0\\p &<0 \end{aligned} | \begin{aligned}x^2 &= 4py \end{aligned} |
Opening to the Right, Opening to the Left | \begin{aligned}p &> 0\\p &<0 \end{aligned} | \begin{aligned}y^2 &= 4px \end{aligned} | |
\begin{aligned}(h, k) \end{aligned} | Opening Upwards, Opening Downwards | \begin{aligned}p &> 0\\p &<0 \end{aligned} | \begin{aligned}(x- h)^2 &= 4p(y – k) \end{aligned} |
Opening to the Right, Opening to the Left | \begin{aligned}p &> 0\\p &<0 \end{aligned} | \begin{aligned}(y –k)^2 &= 4p(x – h) \end{aligned} |
From this we can see that there are four standard forms we can keep in mind and note that the value of $p$ will help us determine whether the parabola is opening upward or downward.
We can use this chart to guide us in finding the vertex, directrix, and focus of the parabola regardless of its orientation, and the translations are done on the parabola.
How to find the vertex of a parabola?
The vertex of a parabola represents the midpoint of the parabola’s focus and directrix. For parabolas that are symmetric vertically, the vertex represents the minimum point of $y$. Meanwhile, parabolas that symmetric horizontally will have a vertex that reflects the minimum point of $x$.
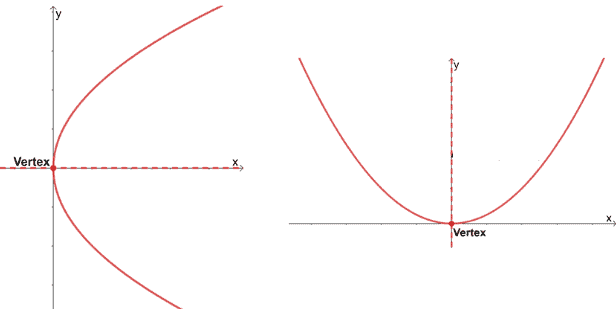
When given the parabola’s graph, it’s easy to spot its vertex, as shown by the graphs above. The parabola’s axis of symmetry also passes through its vertex, so the axis of symmetry will either be $y = k$ and $x = h$, depending on whether $k$ or $h$ is an extreme (minimum or maximum) point of $y$ or $x$, respectively.
The vertex of the parabola can also be easily determined from its equation by writing the equation in standard form and follow the pointers shown below:
Rewrite the equation to make sure it is in standard form.
If the standard form only has $x^2$ or $y^2$, the center is found at the origin so that the vertex will be equal to $(0,0)$.
If we can find a perfect square trinomial, the equation will have a vertex of $(h, k)$.
Use the standard forms of a parabola’s equation (see table above) to determine the value of $h$ and $k$.
How to find the directrix of a parabola?
The directrix is the fixed-line that is found outside the parabola. Given the parabola’s curve, we can find it by moving $p$ units away from the vertex.
If the parabola is opening upward, the directrix is found $p$ units below the vertex.
If the parabola is opening downward, the directrix is found $p$ units above the vertex.
If the parabola is opening to the left, the directrix is found $p$ units to the right of the vertex.
If the parabola is opening to the right, the directrix is found $p$ units to the left of the vertex.
The vertex equation will depend on the value of $p$ from the standard form of the parabola’s equation.
Orientation | Sign of $\boldsymbol{p}$ | Equation of the Directrix |
Parabola is symmetric vertically | $p >0$ | $y = p$ |
$p <0$ | $y = -p$ | |
Parabola is symmetric horizontally | $p >0$ | $x = p$ |
$p <0$ | $x = -p$ |
The directrix is normally represented as a vertical or horizontal dashed line. Having the directrix equation will also tell us the distance, $p$, of the vertex from the focus and the directrix.
How to find the focus of a parabola?
A parabola only has one focus, and it’s located $p$ units away from the vertex and is found within the parabola’s opening.
When given the value of $p$, we can count the $p$ units away from the vertex to locate the position of the focus.
If we’re given the equation of the parabola, we can add $p$ to the vertex’s $x$ or $y$-coordinate depending on its position. The table below can help you find the coordinate of the focus.
Vertex | Equation | Focus |
$(0, 0)$ | $y^2 = 4px$ | $(p, 0)$ |
$(0, 0)$ | $x^2 = 4py$ | $(0, p)$ |
$(h, k)$ | $(y – k)^2 = 4p(x – h)$ | $(h + p, k)$ |
$(h, k)$ | $(x – h)^2 = 4p(y – k)$ | $(h , k + p)$ |
Of course, when $p < 0$, we simplify subtract $p$ from $h$ or $k$. Just make sure to account for its negative sign whenever it’s necessary.
When stuck or you need to quickly remember these properties, a good approach is to use the vertex found in the middle of the focus and the directrix.
Now that we understand each component of parabolas and their equations in standard form, it’s time that we combine all these and start plotting parabolas on $xy$-planes. Don’t forget to quickly recap these components, as we’ll use them extensively in the next section.
How to graph a parabola?
As we have mentioned in the previous sections, parabolas can either open upward, downward, to the left, or to the right. This means that parabolas would look similar as &-shaped curves, but each graph may have a different vertex or orientation.
When given a parabola’s equation, make sure always to write them in standard form so that it’s easier to graph them since we can immediately find important components.
Graphing Parabolas Centered at $\boldsymbol{(0, 0)}$
Let’s begin by exploring the different graphs of parabolas that have a vertex situated at the origin.
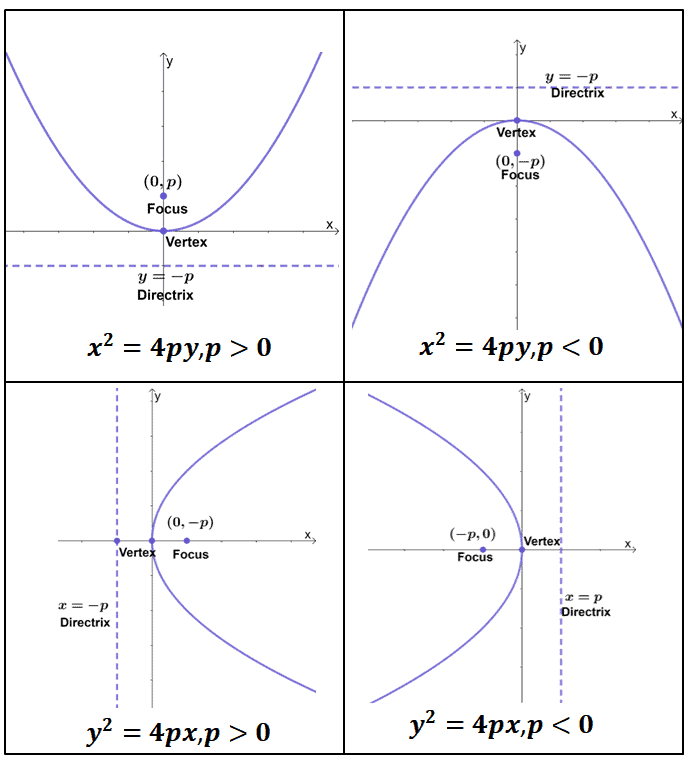
These are the four possible models for parabolas centered at $(0, 0)$. Here are some important reminders when graphing parabolas of these forms:
Take note of the orientation right away by inspecting whether the equation has $x^2$ or $y^2$.
Find the value of $4p$ then eventually solve for $p$.
Plot the vertex and the focus of the parabola.
Identify the location of the directrix as well.
Graph the curve of the parabola after (using extra points as a guide is optional).
Try to assign some values for $p$ and use a table of values to graph these results and confirm that these are indeed the four standard forms’ graphs.
Graphing Parabolas Centered at $\boldsymbol{(h, k)}$
What happens when the parabolas are centered elsewhere? We’ll approach a similar method, but this time, we have to count $p$ units from a vertex, $(h,k)$.
Let’s look at the following models to know how parabolas of these forms will look.
As before, make sure to rewrite the equations so that they are in standard form.
Take note of the orientation right away by inspecting whether the equation has $x^2$ or $y^2$.
Plot the vertex by finding the values of $h$ and $k$.
Factor out the constant from the linear expression and equate the constant to $4p$.
Solve for $p$, then use this to locate the focus and the directrix.
Graph the curve of the parabola after (using extra points as a guide is optional).
As can be seen from the four graphs shown above, we can see that it helps to understand the parabola’s properties to locate the focus and directrix given the parabola’s vertex.
Don’t worry; you’ll be able to graph parabolas in the examples below. Before diving right into these problems, make sure to review your notes and familiarize yourself with important pointers.
Example 1
Let’s use the graph below and our knowledge about parabolas to answer the questions that follow.
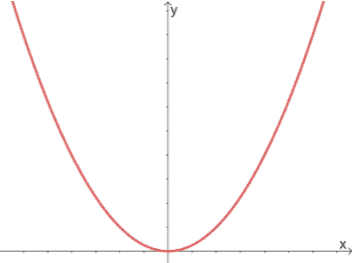
a. What is the standard form of the parabola’s equation?
b. If $4p = 36$, what are the coordinates of the focus?
c. Using the value of $p$ from 1b, what is the equation of its directrix?
Solution
The two important factors to check right away are i) the orientation of the parabola and ii) its vertex.
We can see that parabola is centered at the origin, and since the curve is opening upward, the standard form of the parabola’s equation is $x^2 = 4py$.
Divide both sides of the equation, $4p = 36$, by $4$ to solve for $p$. This represents the distance of the focus and directrix from the parabola’s vertex.
\begin{aligned}4p &= 36\\ p &= 9\end{aligned}
We’re expecting the focus to be $p = 9$ units above the origin, so the coordinates of the focus will be $(0, 0 + 9) = (0, 9)$.
Since the graph is opening upward, we expect the parabola’s directrix to be located $p$ units below the origin. This parabola is symmetric vertically, so we’re expecting the directrix to have an equation of the form, $y = -p$.
This means that the directix’ equation is $y = -9$.
This example clearly demonstrates how we can find the equation and components of parabolas given their graph – it’s extremely helpful when you familiarize yourself with the core definitions of these components.
Example 2
Determine the focus and directrix of the following parabolas given their equations, as shown below.
a. $y^2 = 32x$
b. $x^2 = -24y$
c. $y^2 – 12x= 0$
d. $16x^2 + 8y = 0$
Solution
The first equation’s general form is $y^2 = 4px$. For these types of parabolas, we know the following properties of their components:
The vertex will be found at $(0, 0)$.
In addition, the focus will be at $(p, 0)$ and its directrix will be $x = -p$.
Since $4p =32$, we have $p = 8$. This means that the focus of the parabola is $(8, 0)$ and its directrix will have an equation at $x = -8$.
We’ll apply a similar process for the second equation, but this time, the parabola’s equation’s general form will be $x^2 = 4py$, where $p$ is negative.
This means that the vertex will still be at $(0, 0)$.
The focus will be located at $(0, p)$ and its directrix will be $y = -p$.
Given that $4p = -24$, we have $p = -6$. Using this value, we have the parabola’s focus at $(0, -6)$ and a directrix at $y = -(-6)$ or $y = 6$.
The third is trickier since we’ll need to rewrite it in the parabola’s standard form. We can do this by isolating $y^2$ on the right-hand side.
\begin{aligned}y^2 – 12x &= 0\\ y^2 &= 12x\end{aligned}
We can see that the third equation has a standard form of $y^2 = 4px$. We’ll use a similar process to the first example. Hence, the $p = 3$ and we have the following components:
The third parabola’s focus will be located at $(3,0)$.
The directrix’s equation will be $x = -3$.
Working on the fourth equation, we’ll need to isolate $x^2$ on the equation’s right-hand side.
\begin{aligned}16x^2 + 8y &= 0\\ 16x^2 &=-8y\\x^2 &= -\dfrac{1}{2}y\end{aligned}
This equation has the same general form with the second parabola. We’ll apply a similar process, but this time we have $4p = -\dfrac{1}{2}$, so $p = -\dfrac{1}{8}$.
The fourth parabola’s focus will be found at $\left(0, -\dfrac{1}{8}\right)$.
In addition, the equation of the parabola’s directrix is $y = -\dfrac{1}{8}$.
Example 3
Determine whether the following statements are true or false.
a. The parabola represented by the equation, $y = 2x – x^2 + 6$, will have a graph that opens upward.
b. The graph of the parabola with an equation, $y = ax^2 + bx + c$, will have two $y$-intercepts.
Solution
By inspection alone, we can see that the graph of the parabola either opens upward or downward. Since the sign before $x^2$ is negative, we’re expecting the graph to open downwards.
We can confirm this by rewriting the equation in standard form by moving all the terms with $x$ on the left-hand side and completing the square.
\begin{aligned}y &= 2x – x^2 + 6\\ x^2 – 2x &= -y + 6\\(x^2 – 2x + 1) &= -y + 6 + 1\\ (x – 1)^2 &= -y + 5\\(x- 1)^2 &= -(y – 5)\end{aligned}
a. From this, we can see that the parabola’s graph is oriented vertically, and since $p$ is negative, the graph will open downward. The statement is false.
We’re expecting the graph of $y = ax^2 +bx +c$ to open upwards or downwards depending on the sign of $a$. What we’re sure of is that this parabola will only pass through the $y$-axis once.
b. In fact, its $y$-intercept will be equal to $y = c$. This means that the statement is false.
Example 4
Graph the parabola with an equation of $y^2 = 16x$. Make sure to include the focus and directrix as well.
Solution
The standard form of $y^2 = 16x$ is $y^2 = 4px$, so we can equate $4p$ with $16$ to find the value of $p$.
\begin{aligned}4p &= 16\\ p&= 4\end{aligned}
Parabolas with a standard form of $y^2 = 4px$ will have a vertex at the origin, so let’s use this to count the focus and directrix’ positions.
For this form, the parabola’s focus is $(p, 0)$.
The directrix’s equation will be $x = -p$.
Let’s find two points that lie along the parabola by finding the values of $y$ when $x = p$ or $x = p$.
\begin{aligned}y^2 &= 16(4)\\y^2 &= 64\\ y&= \pm \sqrt{64}\\&= \pm 8\end{aligned}
This means that the parabola passes through $(4, -8)$ and $(4, 8)$. We can then plot the directrix, vertex, focus, and these two points on the coordinate system.
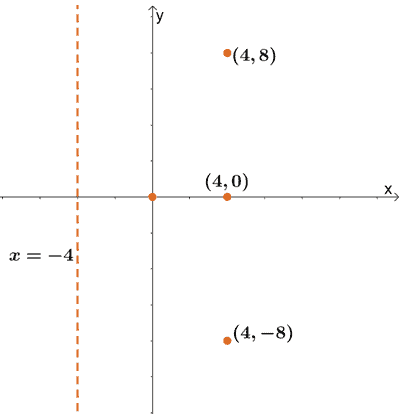
Using the guide points and focus, we can now graph the curve of the parabola that is symmetric along the $x$-axis.
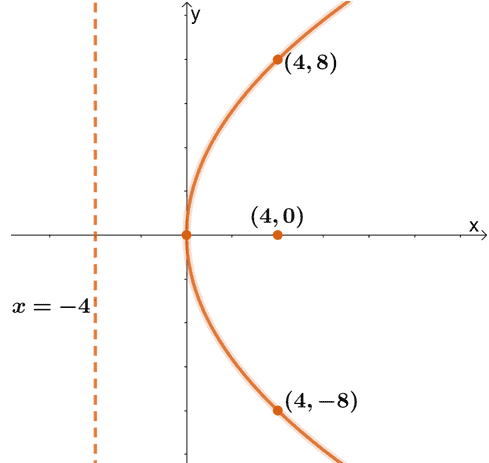
This shows the graph of $y^2 = 16x$ showing the focus at $(4, 0)$ and a diretrix of $x = -4$.
Example 5
Find the equations in the standard form of the following parabolas that satisfy the conditions shown below.
a. A parabola with a focus at $(-6, 0)$ and a directrix at $x = 6$.
b. A parabola with a vertex at $(3, -8)$ and a focus at $(3, -6)$.
c. A parabola with a focus at $(6, -2)$ and a directrix’s equation of $x = 9$.
d. A parabola that has points that are equidistant from $x= 2$ and the point, $(-4, 0)$.
Solution
Since the parabola has a focus that lies along the negative $x$-axis, the vertex of the parabola is at the origin and is opening to the left. This means that the parabola’s standard form is, $y^2 = 4px$, where $p$ is negative.
Since the directrix is $x = 6$ and $p$ will be equal to $-6$. Substitute the value of $p$ into the standard form to find the actual equation of the parabola.
\begin{aligned} y^2 &= 4(-6)x\\y^2&=-24x \end{aligned}
a. This means that the parabola is represented by the equation, $y^2 = -24x$.
The parabola’s vertex will represent $(h, k)$ in its equation’s standard form. Since the focus is located $2$ units right above the vertex, we expect the parabola to open upward.
Hence, the standard form of the parabola will be $(x – h)^2 = 4p(y – k)$, where $(h,k) = (3, -8)$. We’ve mentioned that the distance between the focus and the directrix is $2$ units, so this represents the value of $p$.
Substituting these values for $(h, k)$ and $p$, we have the standard form of the parabola, as shown below.
\begin{aligned} (x – h)^2 &= 4p(y – k)\\ (x – 3)^2 &= 4(2)[y – (-8)]\\(x-3)^2 &= 8(y + 8) \end{aligned}
b. The equation of the parabola is $(x-3)^2 = 8(y + 8)$.
For the third parabola, we can see that the directrix is actually located $3$ units to the right of the focus. This means that the parabola opens to the left, and consequently, its standard form is $(y –k)^2 = 4p(x – h)$, where $p$ is negative.
Since the distance of the vertex from the directrix is $3$ and knowing that $p$ must be negative, $p = -3$. Let’s use this value of $p$ as well as $(h,k) = (6, -2)$ to find the equation of the parabola.
\begin{aligned} (y – k)^2 &= 4p(x – h)\\ [y – (-2)]^2 &= 4(-3)(x-6)\\( y + 2)^2 &= -12(x – 6) \end{aligned}
c. This shows that the equation of the parabola is $( y + 2)^2 = -12(x – 6)$.
For the fourth parabola, since we have $x = 4$ as the directrix, we can see that the parabola either opens to the left or to the right.
The points on the parabola are equidistant from the point, $(0, 4)$, so this point is, in fact, the focus. Knowing this, we can confirm the curve is opening to the right.
The distance between the vertex, $(h, k)$, and the focus will be the same as that of the directrix. We can see that the directrix and the focus are $4$ units apart, so the focus is $\dfrac{4}{2} = 2$ units to the right of the focus.
That’s equal to $(0 + 2, 4) = (2, 4)$. The graph is opening to the left, so $p = -2$ for the standard form, $(y – k)^2 = 4p(x – h)$.
\begin{aligned} (y – k)^2 &= 4p(x – h)\\ (y – 4)^2 &= 4(-2)(x-2)\\( y – 4)^2 &= -8(x – 2) \end{aligned}
d. This means that the parabola’s equation is $(y – 4)^2 = -8(x-2)$.
Example 6
Graph the parabola with an equation of $(y + 4)^2 = 8(x – 2)$. Make sure to include its vertex, focus, and directrix as well.
Solution
By inspection alone, we can see that the parabola’s equation is in standard form, $(y-k)^2 = 4p(x – h)$, where $(h, k)$ is equal to $(2, -4)$ and $4p = 8$.
\begin{aligned} 4p&=8 \\p&=2\end{aligned}
Since it’s $(y + 4)$ that’s squared, we’re expecting the parabola to be symmetric horizontally with the focus and directrix being $p = 2$ units away from the vertex.
This means that the parabola has a focus at $(2 + 2, -4) = (4, -4)$.
It also has a directrix at $x =h – p$ or $x = 0$.
We can also find two points along the parabola’s curve by finding the value of $y$ when $x = 4$.
\begin{aligned}(y + 4)^2 &= 8(x – 2)\\ &= 8(4 – 2)\\&= 16\\\\ y + 4&= \pm \sqrt{16}\\y&=-4 \pm 4\\&= \{0, -8\}\end{aligned}
This means that the parabola passes through the points, $(4, -8)$ and $(4, 0)$. Let’s go ahead and plot these components of the parabola first.
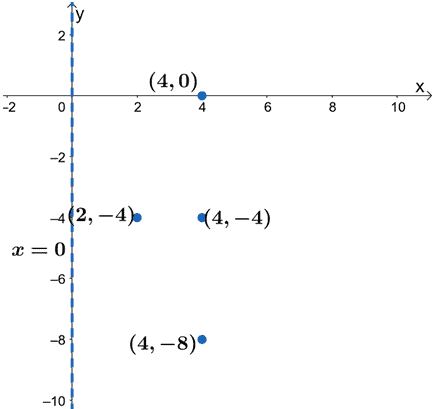
We can then graph the parabola that is opening to the right and is symmetric horizontally. Make sure that the parabola passes through the two points and has the focus at its opening.
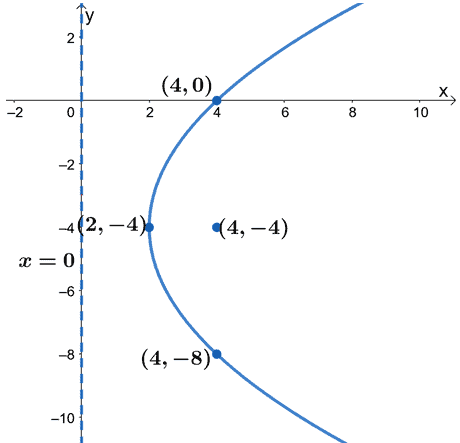
This shows the graph of $(y + 4)^2 = 8(x – 2)$ showing the focus at $(4, -4)$, vertex at $(2, -4)$, and a directrix of $x = 0$.
Example 7
Write the parabola’s equation, $2x^2 + 16x – 8y + 16 = 0$, in standard form.
a. Determine the parabola’s vertex, directrix, and focus.
b. Graph the parabola’s curve and include components in 6a.
c. Based on the graph, find the domain and range of the parabola.
d. What does the vertex of the parabola represent?
Solution
First, let’s rewrite the equation to perform the following steps in standard form.
Dividing both sides of the equation by $2$.
Since we have a squared term for $x$, we leave all terms with $x$ on the equation’s left-hand side.
Complete the square for the left-hand side and ensure that the equation is intact by adding the same constant on the right-hand side.
\begin{aligned}2x^2 + 16x – 8y + 16 &= 0\\x^2 + 8x – 4y + 8 &=0\\(x^2 + 8x \phantom{xxxx})& = 4y – 8\\(x^2 + 8x + 16) &= 4y – 8 + 16\\(x^2 + 8x + 16) &= 4y + 8\end{aligned}
We’re still halfway through the process – make sure that it is of the form, $(x – h)^2 = 4py$.
Express the left-hand side in factored form.
Factor out the constant on the right-hand side expression.
\begin{aligned}(x + 4)^2 &= 4y + 8\\(x + 4)^2 &= 4(y + 2)\end{aligned}
Now that the equation is in standard form, we can now determine the parabola’s important components.
The vertex of the parabola is located at $(-4, -2)$.
Since $4p = 4$, the distance of the vertex from the focus and the directrix is $p = 1$ unit.
Since $p$ is positive and it’s $(x + 4)$ that is squared, the parabola is open u, so the focus is $(-4, -2+1) = (-4, -1)$ and the directrix will be $y = -3$.
We can find two more points that lie along the parabola’s curves by finding the value of $x$ when $y = -1$.
\begin{aligned}(x+ 4)^2 &= 4(y + 2)\\ &= 4(-1 + 2)\\&= 4\\\\ x + 4&= \pm \sqrt{4}\\x&=-4 \pm 2\\&\approx \{-6, -2\}\end{aligned}
Let’s plot the vertex, focus, and directrix, and these two points guide us in graphing the parabola.
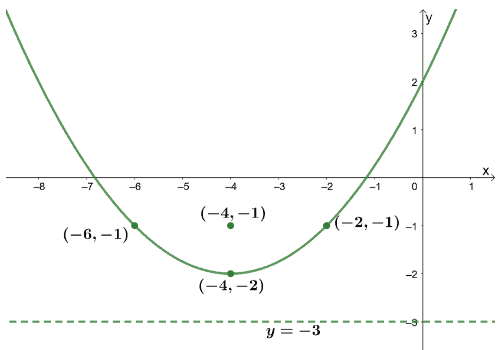
Without the guide points, you’ll be able to have the graph of $2x^2 + 16x – 8y + 16 = 0$ or $(x+ 4)^2 = 4(y + 2)$ with the parabola’s focus, vertex, and directrix.
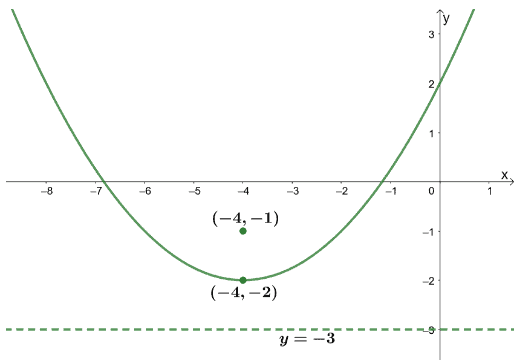
Let’s observe the finalized graph to determine the parabola’s domain and range.
We can see that the graph extends on both sides of $x$ so that the domain will be all real numbers or $\{x|x \in \mathbb{R}\}$.
The lowest point of the parabola shown is its vertex, so the range can be any value of $y$ that is greater than or equal to $-1$ or algebraically, \{y|y \geq-1\}.
As mentioned in the previous bullet, the vertex, $(-4, -2)$, is the parabola’s lowest point and, consequently, the function’s minimum value.
Example 8
James runs a company that installs satellite dishes with a parabolic surface that opens upward. The diameter of the dish is $25$ feet and has a depth of $5$ feet. If the receiver of the satellite acts as the focus of the parabolic satellite dish:
a. What is the distance of the receiver from the base of the satellite dish?
b. How will the receiver’s position be affected if the graph’s diameter is doubled, but the depth remains the same?
Solution
For word problems involving parabolas (or conics, in general), it’s helpful to construct a diagram that models the situation.
We can construct a parabola that is $25$ feet wide, and that opens upward.
We can situate the vertex at the origin so that it’ll be faster for us.
Since the depth is $5$ feet throughout, it is safe for us to assume that the parabola contains $(5, 25)$.
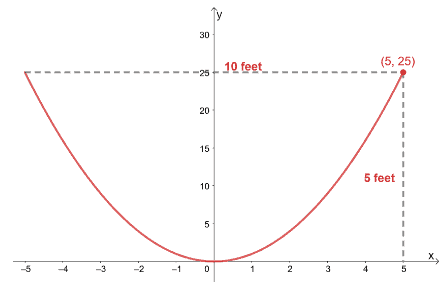
We can see that the standard form of this parabola’s equation is $x^2 = 4py$. We can use the endpoint, $(5, 25)$, to find the value of $p$.
\begin{aligned}x^2 &= 4py\\ 5^2 &= 4p(25)\\25 &= 100p\\p&= \dfrac{1}{4}\end{aligned}
Since $p = \dfrac{1}{4}$ pr $p = 0.25$, we can find the focus of the parabola – $(0, p)$. This means that the focus is $(0, 0.25)$.
a. The receiver is positioned at the focus, so we can see that it’s $0.25$ feet from the satellite dish’s base.
Let’s go ahead and draw another diagram – this time, the base of the parabola is widened twice its original width.
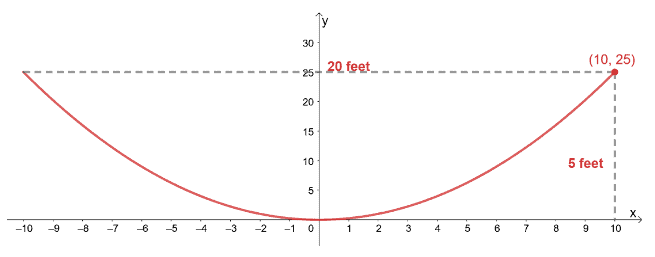
The vertex will remain the same, so the standard form will still be $x^2 = 4py$. We’ll use $(10, 25)$ this time, though, so we’ll expect a new value for $p$.
\begin{aligned}x^2 &= 4py\\ 10^2 &= 4p(25)\\ 100 &= 100p\\ p&= 1\end{aligned}
From this, we can see that from $p_{\text{old}} = \dfrac{1}{4}$ and $p_{\text{new}} = 1$. The receiver will now be positioned $1$ foot above the vertex.
b. This means that the receiver’s height from the satellite’s dish is increased four times and is now equal to $1$ foot.
Practice Questions
![]()
Open Problems
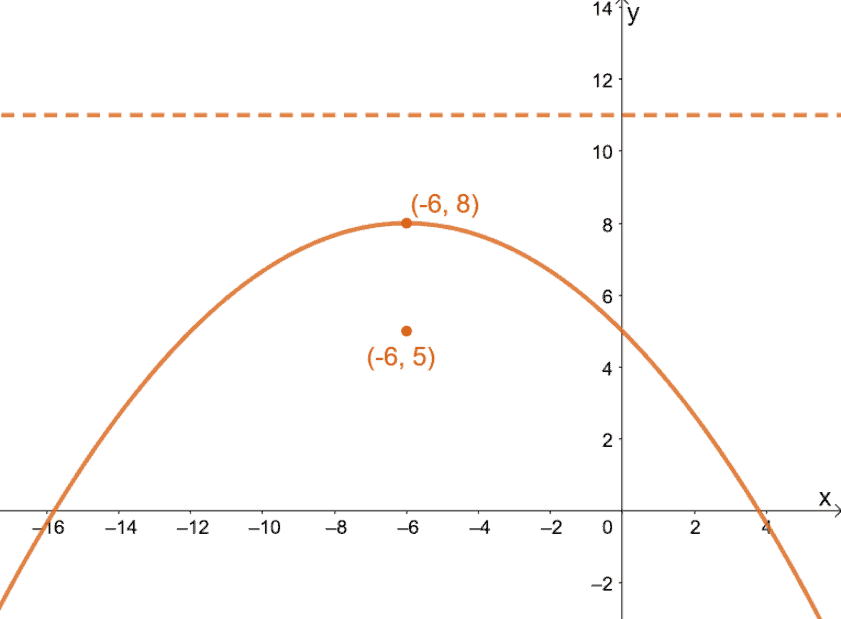
1. Graph the parabola with an equation of $(x + 6)^2 = -12(y – 8)$.
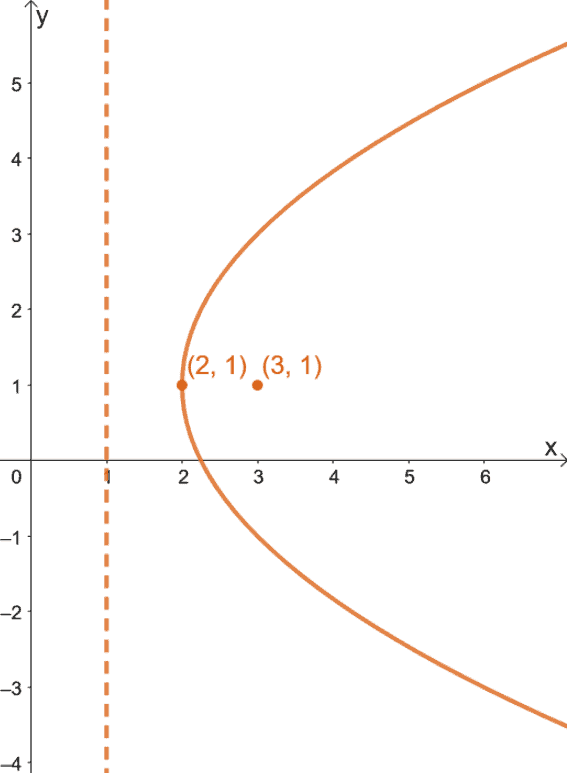
2. Graph the parabola with an equation of $3y^2 – 6y – 12x + 27 = 0$.
Open Problem Solutions
1.
2.
Images/mathematical drawings are created with GeoGebra.
