Parallel Lines – Definition, Properties, and Examples

When working with parallel lines, it is important to be familiar with their definition and properties. Let’s go ahead and begin with its definition.

                      Parallel lines are lines that are lying on the same plane but will never meet.

Understanding what parallel lines are can help us find missing angles, solve for unknown values, and even learn what they represent in coordinate geometry.

Since parallel lines are used in different branches of math, we need to master them as early as now.

What are the parallel lines?

Parallel lines are equidistant lines (lines having equal distance from each other) that will never meet.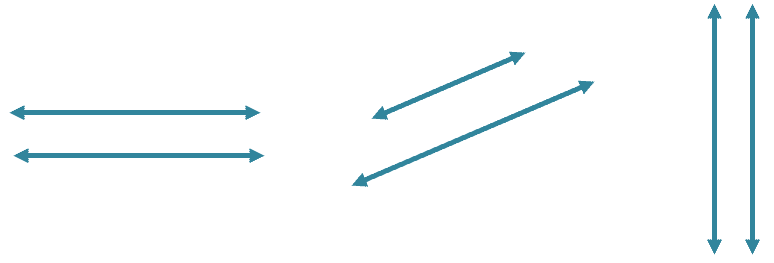
These are some examples of parallel lines in different directions: horizontally, diagonally, and vertically.

Another important fact about parallel lines: they share the same direction.

What are some real-world examples of parallel lines?

• Roadways and tracks: the opposite tracks and roads will share the same direction, but they will never meet at one point.
• Lines on a writing pad: all lines are found on the same plane, but they will never meet.
• Pedestrian crossings: all painted lines lie along the same direction and road, but these lines will never meet.

How do we use parallel lines in coordinate geometry?

• When the graphs of two linear equations are parallel in coordinate geometry, the two equations do not share a solution.
• The slopes of two parallel lines are equal in coordinate geometry.

We’ll learn more about this in coordinate geometry, but for now, let’s focus on the parallel lines’ properties and using them to solve problems.

How to prove lines are parallel?

Several geometric relationships can be used to prove that two lines are parallel.

Before we begin, let’s review the definition of transversal lines.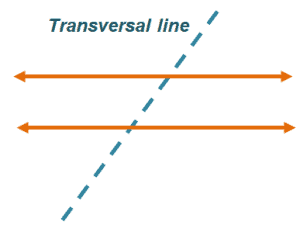

Transversal lines are lines that cross two or more lines.

The image shown to the right shows how a transversal line cuts a pair of parallel lines.

When a transversal line cuts a pair of parallel lines, different pairs of angles are formed. These different types of angles are used to prove whether two lines are parallel to each other.

In the next section, you’ll learn what the following angles are and their properties:

•  Corresponding angles
• Alternate interior angles
• Alternate exterior angles
• Consecutive interior angles

Properties of parallel line

When a transversal line cuts two lines, the properties below will help us determine whether the lines are parallel.

1. Two lines cut by a transversal line are parallel when the corresponding angles are equal.

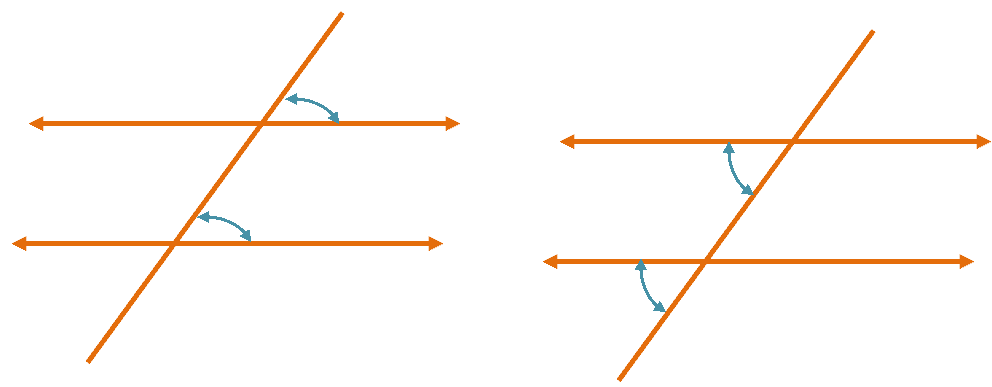
The two pairs of angles shown above are examples of corresponding angles. In general, they are angles that are in relative positions and lying along the same side.

2. Two lines cut by a transversal line are parallel when the alternate interior angles are equal.

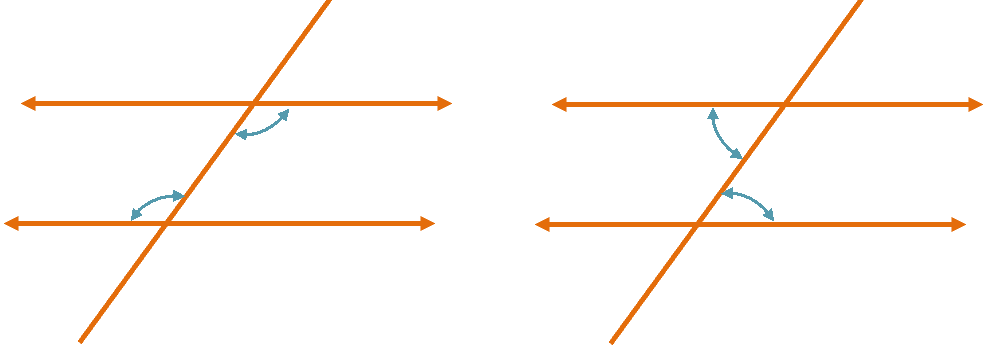
Alternate interior angles are a pair of angles found in the inner side but are lying opposite each other.

3. Two lines cut by a transversal line are parallel when the alternate exterior angles are equal.

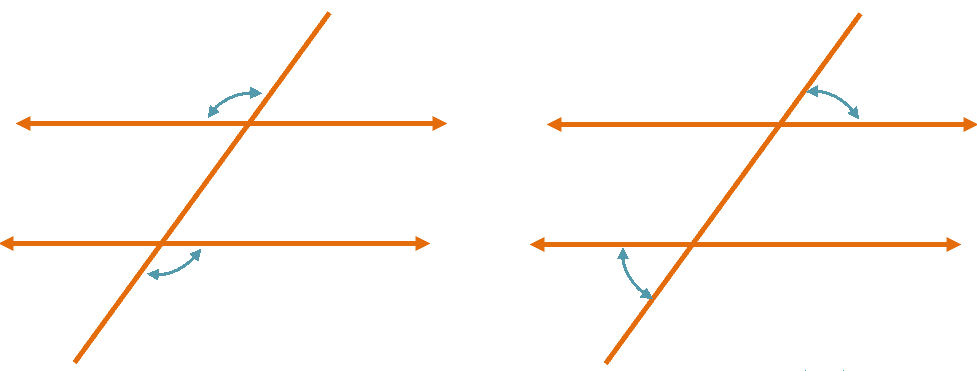
Alternate exterior angles are a pair of angles found on the outer side but are lying opposite each other.

4. Two lines cut by a transversal line are parallel when the sum of the consecutive interior angles is $\boldsymbol{180^{\circ}}$.

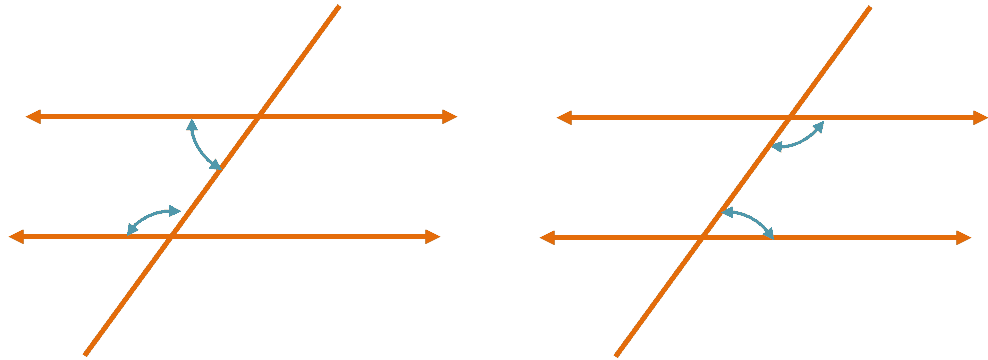
Consecutive interior angles are consecutive angles sharing the same inner side along the line.

5. Two lines cut by a transversal line are parallel when the sum of the consecutive exterior angles is $\boldsymbol{180^{\circ}}$.

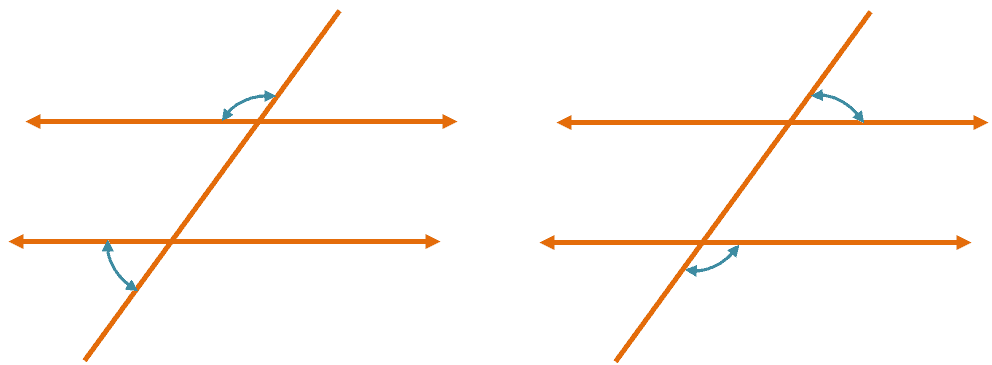
Consecutive exterior angles are consecutive angles sharing the same outer side along the line.

Summary of parallel lines definition

Let’s summarize what we’ve learned so far about parallel lines:

• they are coplanar lines
• they are equidistant
• they will never meet

The properties below will help us determine and show that two lines are parallel.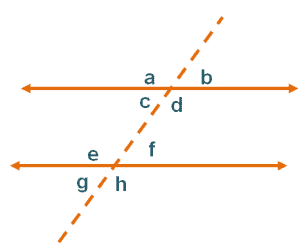

1.  Corresponding angles are equal.

Example: $\angle b ^{\circ} = \angle f^{\circ}, \angle a ^{\circ} = \angle e^{\circ}e$

2. Alternate interior angles are equal.

Example: $\angle c ^{\circ} = \angle f^{\circ}, \angle d ^{\circ} = \angle e^{\circ}$

3. Alternate exterior angles are equal.

Example: $\angle a ^{\circ} = \angle h^{\circ}, \angle b^{\circ} = \angle g^{\circ}$

4. Consecutive interior angles add up to $180^{\circ}$.

Example: $\angle c ^{\circ} + \angle e^{\circ}=180^{\circ}$, $\angle d ^{\circ} + \angle f^{\circ}=180^{\circ}$

5. Consecutive exterior angles add up to $180^{\circ}$.

Example: $\angle a^{\circ} + \angle g^{\circ}=$180^{\circ}$, $\angle b ^{\circ} + \angle h^{\circ}=180^{\circ}$

Let’s try to answer the examples shown below using the definitions and properties we’ve just learned.

Example 1

Which of the following term/s does not describe a pair of parallel lines?

a. Noncoplanar

b. Coplanar

c. Equidistant

d. Same direction

Solution

Go back to the definition of parallel lines: they are coplanar lines sharing the same distance but never meet. This shows that parallel lines are never noncoplanar.

Example 2

Which of the following real-world examples do not represent a pair of parallel lines?

a. Hands of a clock

b. Windscreen wipers

c. Staircase and railings

d. Vertical strings of a tennis racket’s net

Solution 

The options in b, c, and d are objects that share the same directions, but they will never meet. They all lie on the same plane (i.e., the strings lie in the same plane of the net).

However, the hands of a clock meet at the center of the clock, so a pair of parallel lines will never represent them.

Hence, the correct answer is a.

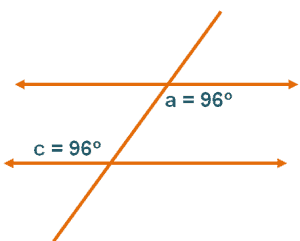
Example 3

Are the two lines cut by the transversal line parallel?  What property can you use to justify your answer?

Solution

The two lines are parallel if the alternate interior angles are equal.

Since $a$ and $c$ share the same values, $a = c$.  The two angles are alternate interior angles as well.
This shows that the two lines are parallel.

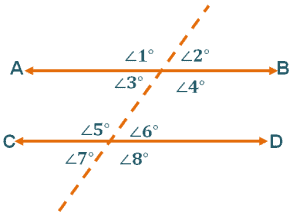
Example 4

If the lines $\overline{AB}$ and $\overline{CD}$ are parallel and $\angle 8 ^{\circ} = 108 ^{\circ}$, what must be the value of $\angle 1 ^{\circ}$?

Solution

Since the lines are parallel and $\angle 1 ^{\circ}$ and $\angle 8 ^{\circ}$ are alternate exterior angles, $\angle 1 ^{\circ} = \angle 8 ^{\circ}$.

This means that $\boldsymbol{\angle 1 ^{\circ}}$ is also equal to $\boldsymbol{108 ^{\circ}}$.

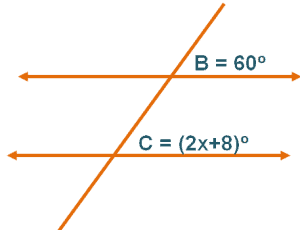
Example 5

If the two lines are parallel and cut by a transversal line, what is the value of $x$?

Solution

Since the lines are parallel and $\boldsymbol{\angle B}$ and $\boldsymbol{\angle C}$ are corresponding angles, so $\boldsymbol{\angle B = \angle C}$.

Equate their two expressions to solve for $x$.

$60 = 2x + 8$

Isolate $2x$ on the left-hand side of the equation.

$2x = 60 – 8$

$2x = 52$

Divide both sides of the equation by $2$ to find $x$.

$x = 26$

This means that $\boldsymbol{x = 26}$.

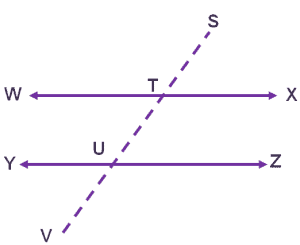
Example 6

If ∠WTS and∠YUV are supplementary (they share a sum of 180°), show that WX and YZ are parallel lines.

Solution

The angles $\angle WTS$ and $\angle YUV$ are a pair of consecutive exterior angles sharing a sum of $\boldsymbol{180^{\circ}}$.

Recall that two lines are parallel if its pair of consecutive exterior angles add up to $\boldsymbol{180^{\circ}}$. Hence,  $\overline{WX}$ and $\overline{YZ}$ are parallel lines.

Example 7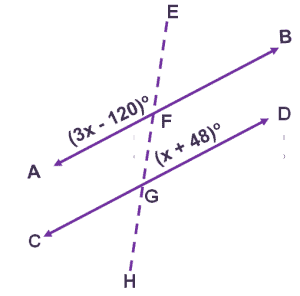

If $\overline{AB}$ and $\overline{CD}$ are parallel lines, what is the actual measure of $\angle EFA$?

Solution

The angles $\angle EFB$ and $\angle FGD$ are a pair of corresponding angles, so they are both equal.

This means that $\angle EFB = (x + 48)^{\circ}$.

The angles  $\angle EFA$ and $\angle EFB$ are adjacent to each other and form a line. They add up to  $\boldsymbol{180^{\circ}}$. 

Use this information to set up an equation and we can then solve for $x$.

$\angle EFB + \angle EFA= 180^{\circ}$

$(x + 48) ^{\circ} + (3x – 120)^{\circ}= 180 ^{\circ}$

Add the two expressions to simplify the left-hand side of the equation.

$x + 48 + 3x – 120 = 180$

$4x – 72 = 180$

Add $72$ to both sides of the equation to isolate $4x$.

$4x = 252$

Divide both sides of the equation by $4$ to find $x$.

$x = 63$

Substitute this value of $x$ into the expression for $\angle EFA$ to find its actual measure.

$\begin{aligned}3x – 120 &= 3(63) – 120\\ &=69\end{aligned}$

This means that the actual measure of $\angle EFA$  is $\boldsymbol{69 ^{\circ}}$.

Example 8

If $\angle 1 ^{\circ}$ and  $\angle 8 ^{\circ}$ are equal, show that  $\angle 4 ^{\circ}$ and  $\angle 5 ^{\circ}$ are equal as well.

Solution

The angles $\angle 1 ^{\circ}$ and  $\angle 8 ^{\circ}$ are a pair of alternate exterior angles and are equal.

Recall that two lines are parallel if its pair of alternate exterior angles are equals. Hence,  $\overline{AB}$ and $\overline{CD}$ are parallel lines.

Now that we’ve shown that the lines parallel, then the alternate interior angles are equal.

The angles $\angle 4 ^{\circ}$ and $\angle 5 ^{\circ}$ are alternate interior angles inside a pair of parallel lines, so they are both equal.