Parallel Planes – Explanation & Examples

Want to know more about parallel planes? This article is a great source of information about parallel planes, their properties, and their application. Let’s start with recalling what parallel planes are:

                                        Parallel planes are planes that never intersect.

Need some refresher? You can check out the following links:

• Learn about planes and polygons.
• Learn about parallel lines.

These concepts were extended to parallel planes. In the next sections, we’ll learn how to:

• define parallel lines
• find parallel planes from a figure
• verify whether two planes (from equations) are parallel

What are parallel planes?

As mentioned in the first section, when two planes lie in the same direction but do not meet, we call them parallel planes.

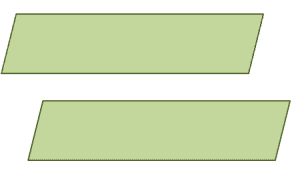
The figure above shows an example of two parallel planes. Observe how the two extends in the same direction, but these planes will never meet.

What do we call planes that intersect? Yes, you guessed it right. Planes that are not parallel and intersect along a line are called intersecting planes.

What are some real-world examples of parallel planes?

• Our homes’ ceilings and floors are great examples of parallel planes. They extend along with the same space (our home), but these two planes will never meet.
• The steps on our stairs are also examples of parallel planes. Each step extends along the same direction as one another, but these steps will never intersect each other.
• Two bookshelves facing each other are another great example of parallel planes.

We’ve now learned about parallel planes, so it’s time for us to practice looking for parallel planes in three-dimensional figures.

How to determine if planes are parallel?

To identify parallel planes, we have to ensure that the planes we’re comparing are lying along with the same space. Look for a reference plane and find a second plane that is facing opposite it.

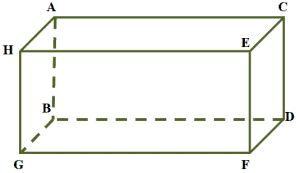
The rectangular prism shown above contains multiple pairs of parallel planes. To find one pair, we can start with Plane $\boldsymbol{ABCD}$. Find the surface lying in the same direction, but opposite to it, and that will be Plane $\boldsymbol{HEFG}$.

Since both planes are within the same prism, we can say that the two are parallel to each other or Plane $\boldsymbol{ABCD ||}$ Plane $\boldsymbol{HEFG}$.

How to check if the equations of two planes are parallel?

• In coordinate geometry, when the graphs of equations of the form $A_x + B_y + C_z = D$ are parallel, the two equations’ dot product is zero.
• Given two equations, $A_1x + B_1y + C_1z = D_1 $ and $A_2x + B_2y + C_2z = D_2$, the two planes are parallel when the ratios of each pair of coefficients are equal.

$ \dfrac{A_1}{A_2}=\dfrac{B_1}{B_2}=\dfrac{C_1}{C_2}$

We can even determine the distances between two parallel planes, but we’ll learn more about this when we study higher coordinate geometry and vectors.

For now, let’s focus on the parallel planes’ fundamental definitions, and let’s practice identifying parallel planes in three-dimensional figures.

Summary of parallel planes definition and properties

Before we start checking our new knowledge on parallel planes, let’s make sure we summarize everything that we know so far:

• Parallel planes lie along with the same space.
• These planes can never meet.
• We can apply the transitive property to parallel planes.
• Equations that represent planes are parallel when the ratios of their terms’ coefficients are equal.

Example 1

Which of the following is not true about parallel planes?

1. They share the same space.
2. They lie in the same direction.
3. Their intersection is a line.
4. They will never meet.

Solution

Go back to the definition of parallel planes: they share the same space and will never meet. Planes that do meet are called intersecting planes. When they do, they intersect through a line. This means that parallel planes will never intersect at a line.

Example 2

Which of the following are examples of parallel planes?

1. A writing pad’s cover and its page.
2. The surfaces of a triangular tent.
3. A library’s ceiling and floor.
4. The corner of a room.

Solution

Let’s discuss each example shown and see if they satisfy the conditions of parallel planes:

• The writing pad’s cover and pages share a common side and are glued or stapled there, so they stick together. This means that they are not parallel planes.
• A triangular tent will not have surfaces that lie along the same direction, and each pair of planes share a common side.
• The corner of a room share a common side, so they do not represent parallel planes.

However, the library’s ceiling and floor are in the same direction and space, but they will never meet. This means that the third option is the correct answer.

Example 3

Take a snippet or a screenshot of the problem and construct a second plane so that you now have a pair of parallel planes.

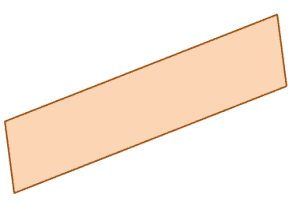
Solution

Since parallel planes extend along the same direction, draw either a plane above or below the given one. Make sure that the two planes will never meet so that they satisfy the conditions of parallel planes.

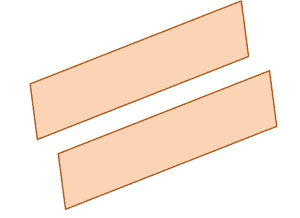
The figure shown above is an example. Yours might look different, but as long as they meet the conditions, they are valid answers.

Example 4

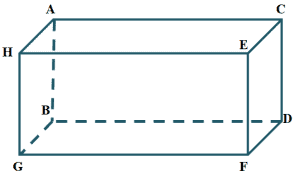
List down three pairs of parallel planes you can find in the figure shown below.

Solution

Rectangular prisms have six surfaces, so it makes sense that it has three pairs of parallel planes.

Let’s start with Plane $\boldsymbol{ABCD}$, the surface lying opposite it is Plane $\boldsymbol{HEFG}$. This means that these two planes are parallel. We can do the same for the two remaining pairs.

Plane $\boldsymbol{HABG}$ and Plane $\boldsymbol{ECDF}$ are facing opposite each other. The third pair, Plane $\boldsymbol{ACEH}$ and Plane $\boldsymbol{BDFG}$  are also facing opposite each other. Hence, we have the following pairs of parallel planes:

• $Plane\ \boldsymbol{ABCD ||} Plane \ \boldsymbol{HEFG}$
• $Plane\ \boldsymbol{HABG || }Plane\ \boldsymbol{ECDF}$
• $Plane\ \boldsymbol{ACEH || }Plane\ \boldsymbol{BDFG}$

Example 5

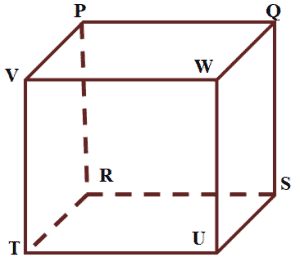
Which of the following pairs of planes are parallel to each other?

1. $\boldsymbol{PQWV}$ and $\boldsymbol{PQRS}$
2. $\boldsymbol{VWUT}$ and $\boldsymbol{RSUT}$
3. $\boldsymbol{VWUT}$ and $\boldsymbol{PQRS}$
4. $\boldsymbol{PVTR}$ and $\boldsymbol{RSUT}$

Solution

Recall that parallel planes do not intersect and share the same side. Observe the three pairs: $\boldsymbol{PQWV}$ and $\boldsymbol{PQRS}$, $\boldsymbol{VWUT}$ and $\boldsymbol{RSUT}$, as well as $\boldsymbol{PVTR}$ and $\boldsymbol{RSUT}$.

• $\boldsymbol{PQWV}$ and $\boldsymbol{PQRS}$ intersect each other at their common side, $\boldsymbol{PQ}$.
• $\boldsymbol{VWUT}$ and $\boldsymbol{RSUT}$ intersect each other at their common side, $\boldsymbol{UT}$.
• $\boldsymbol{PVTR}$ and $\boldsymbol{RSUT}$ intersect each other at their common side,$\boldsymbol{RT}$

This means that the only possible pair of parallel lines are $\boldsymbol{VWUT}$ and $\boldsymbol{PQRS}$. We can also see that the two faces opposite each other, confirming that they are the correct option.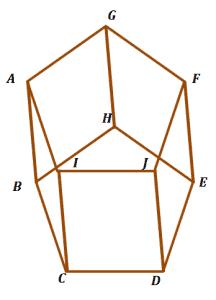

Example 6

Does the figure below contain any parallel planes?

Name one pair and describe its shape.

Solution

The bases lie in the same direction and will never meet. They also do not share a common side. This means that the figure contains a pair of parallel planes.

Planes AGFJI and BHEDC each contain five sides. Pentagons are polygons that contain five sides, so the parallel planes are parallel pentagons.

Example 7

Determine whether the planes, $4x – 5y + 2z = 5$ and $8x -10y + 4z = 12$ , are parallel.

Solution

Recall that two planes are parallel when the ratios of their coefficients share the relationship shown below.

$\dfrac{A_1}{A_2}=\dfrac{B_1}{B_2}=\dfrac{C_1}{C_2}$

Substitute the coefficients and find their respective ratios:

• $A_1 = 4$, $A_2= 8$, $\dfrac{A_1}{A_2}=2$
• $B_1 = -5$, $B_2=10$, $\dfrac{B_1}{B_2}= 2$
• $C_1 = 2$, $C_2 =4$, $\dfrac{C_1}{C_2}=2$

We can see that the ratios are equal, so the two planes are parallel.

Example 8

What must be the value of $a$ so that the planes shown below are parallel?

$3x – 4y + z = 4$

$6x – (a + 2) y + 2z = 9$

Solution

Recall that two planes are parallel when the ratios of their coefficients share the relationship shown below.

$\dfrac{A_1}{A_2}=\dfrac{B_1}{B_2}=\dfrac{C_1}{C_2}$

Substitute the coefficients and find their respective ratios:

• $A_1 = 3$, $A_2=6$,  $\dfrac{A_1}{A_2}=\dfrac{1}{2}$
• $B_1=4$, $B_2=a + 2$,  $\dfrac{B_1}{B_2}=\dfrac{4}{a + 2}$
• $C_1 = 1$, $C_2=2$, $\dfrac{C_1}{C_2}=\dfrac{1}{2}$

For the planes to be parallel, the three ratios must be equal. This means that $\dfrac{4}{a + 2}$ must be equal to $\dfrac{1}{2}$. Equate the two and solve for $a$.

$\dfrac{4}{a + 2} = \dfrac{1}{2}$

Cross-multiply and simplify the expressions on both sides of the equation.

$ \begin{aligned}4(2)&=1(a+2)\\8 &= a + 2\\ a &= 8 – 2\\ a &= 6\end{aligned}$

This means that $a$ must be $6$ for the two planes to be parallel.