- Home
- >
- Permutation – Explanation & Examples
JUMP TO TOPIC
Permutation – Explanation & Examples
Many interesting questions in probability theory require us to calculate the number of ways You can arrange a set of objects.
For example, if we randomly choose four alphabets, how many words can we make? Or how many distinct passwords can we make using $6$ digits? The theory of Permutations allows us to calculate the total number of such arrangements.
Permutation refers to the possible arrangements of a set of given objects when changing the order of selection of the objects is treated as a distinct arrangement.
After reading this article, you should understand:
- Permutation
- How to do a Permutation
- Formula and different representations of permutation in mathematical terms.
- Types of permutations
- Solving problems related to permutations
It is advisable to refresh the following concepts to understand the material discussed in this article.
What Is a Permutation
Generally speaking, permutation means different possible ways in which You can arrange a set of numbers or things. In mathematics, permutation is a technique that determines the number of possible ways in which elements of a set can be arranged. For Example, the permutation of Set $Z= \{1,2\}$ is $2$, i.e., $\{1,2\}$ and $\{2,1\}$. We can see from this example that these are the only two possibilities in which the elements can be arranged.
How to do a permutation
To understand how to do a permutation, we first have to understand the concepts of a factorial and the concept of the fundamental counting principle. Both concepts are briefly discussed below.
Factorial
Let $a$ be a positive integer. Then the product $a \times (a-1) \times (a-2) \times (a-3) \times \cdots 3 \times 2 \times 1$ is donated by $\textrm{a! }$ and it is read as $a$ factorial.
For example
$1! = 1$
$2! = 2 \times 1 = 2$
$3! =3 \times 2 \times 1 = 6$
$7! = 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 5040$
Also, $0!$ is defined to be equal to one.
Let us evaluate some problems to get a firm grip of factorial
Example 1: Evaluate $ \frac{6!}{3!}$
solution:
$ = \frac{6 \times 5 \times 4 \times 3 \times 2 \times 1}{3 \times 2 \times 1}$
$ = (6 \times 5 \times 4)$
$ = 120$
Example 2: Evaluate $\frac{7!}{2!(7-2)!}$
Solution:
$ = \frac{7 \times 6 \times 5!}{2! \times 5!}$
$ = \frac{7 \times 6}{(2 \times 1)}$
$ = \frac{42}{2}$
$ = 21$
Example 3: Evaluate $\frac{11!}{5!\times 6!}$
Solution:
$ = \frac{11 \times 10 \times 9 \times 8 \times 7 \times 6!}{5! \times 6!}$
$ = \frac{11 \times 10 \times 9 \times 8 \times 7}{5 \times 4 \times 3 \times 2 \times 1}$
$ =\frac{55440}{120}$
$ = 462$
The Counting Principle
The counting principle is a rule to count the number of possible arrangements for a given statement or problem. For example, if $X$ and $Y$ are two events and the event $X$ can occur in $A$ different ways and the event $Y$ can occur in $B$ different ways, then the number of events in which two events can occur is $A \times B$. Suppose that you want to make a sandwich for yourself and you have two kinds of bread available in the kitchen, brown and white bread. You have the option to fill both of the bread either with chicken or vegetable material. How many possible sandwiches can be made?
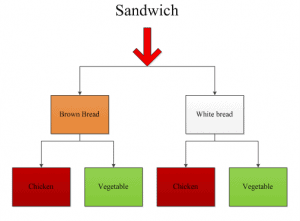
As the tree diagram shows, you can make two types of sandwiches from brown bread and two types of sandwiches from white bread, and in total, you can make a total of four sandwiches. Let $X$ be the brown bread and $Y$ be the white bread. $X$ can be used to make two sandwiches, so $A=2$ and similarly $Y$ can be used to make two sandwiches $B=2$. Total number of possible events $A \times B= 2 \times 2 =4 $.
Permutation Examples
Now that we know how to evaluate a factorial and how the counting principle works, we can consider a few examples of permutations. A simple example of permutation would be the arrangement of four different cups in a cupboard on a single shelf having four slots.
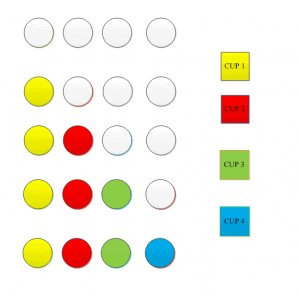
A simple explanation is that the first cup can be arranged in any of the given four slots, so it has four choices. Similarly, we have then 3 choices remaining for the second cup, 2 choices for the second last cup, and 1 choice for the last cup. So, multiplying $4 \times 3 \times 2 \times 1= 24$ ways in which we can arrange all the cups. This can also be calculated as $4!= 4 \times3 \times 2 \times 1 = 24 $.
For the second example, consider a triangle with vertices X, Y, and Z.
Given below is a picture of all possible triangles which can be formed by using these vertices.
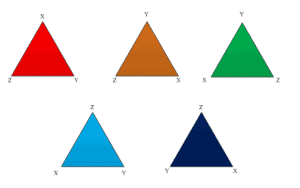
So, we have six different ways of naming the triangle. XYZ, XZY, YZX, YXZ, ZXY and ZYX
Explanation: If the first vertex is named “X,” so now we have two vertices remaining. If the second one is named “Y,” then the last one has to be named “Z,” and we get triangle XYZ. Similarly, if we keep “X” as the first Vertex and the second one is named “Z,” then the last one has to be named “Y” by doing so, we get the triangle “XZY.” Repeating the exercise by changing vertices names, we get six possible triangles.
Alternative Solution: Consider we have an un-named triangle at the start so, at the start, we can name any of the three vertices as ‘X,” and after that two vertices are left so, we can write the “Y” in 2 different ways while we can write the last vertex in only one way.
So, the total number of possible arrangements is a product of $3 \times 2 \times 1= 6$.
Permutation Definition
Permutation refers to the possible arrangements of a set of given objects when changing the order of selection of the objects is treated as a distinct arrangement.
Permutation Formula
A permutation of $n$ different objects taken $r$ at a time where $r ≤ n$ is given as
$ P(n,r) = \frac{n!}{(n-r)!} $
Derivation
Suppose that we have $n$ different boxes to fill up $r$ places.
The first place can be filled with $n$ different boxes
The second place can be filled with $(n-1)$ boxes
The third-place can be filled with $(n-2)$ boxes
The fourth place can be filled with $(n-3)$ boxes
The rth place can be filled with $(n-(r-1))$. Therefore, by counting principle $r$ places can be filled with n boxes in $n \times (n-1) \times (n-2) \times \cdots \times (n-r+1)$ ways.
$ P(n,r) = n \times (n-1) \times (n-2) \times \cdots \times (n-r+1)$
Now multiplying and dividing by$ (n-r)!$ we get,
$ P(n,r) = \large{\frac{n \times (n-1) \times \cdots \times 3 \times 2 \times1}{(n-r) \times (n-r-1) \times \cdots \times 2 \times 1}}$
After simplification, we get
$ P(n,r) = \frac{n!}{(n-r)!} $
In both the examples above, the maximum possible objects were selected during the calculation of permutation, i.e., in both the examples, $n$ was equal to $r$. In the cupboard example, we had four available cups, and the slots available were also four, and in the case of the triangle, we had three vertices for 3 sides of the triangle. Let us now discuss an example where $r$ is less than $n$.
Consider Set $A = { 1,2,3,4,5,6,7,8,9}$. Set $A$ has nine elements and you are required to give possible arrangements for only four of them. So, $n = 9$ while $r = 4$.
$ P(n,r) = \frac{n!}{(n-r)!} $
$ P(9,4) = \frac{9!}{(9-4)!} $
$ P(9,4) = \frac{9!}{5!}$
$ P(9,4) = \frac{9\times 8\times7\times6\times5\times4\times3\times2\times1}{54 \times3 \times2 \times1} $
$ P(9,4) = 3024$ possible arrangements
When to Use Permutation
The permutation is used whenever we are interested in finding the total number of possible arrangements of a given set and when the order of selection matters, i.e., different orders of selection result in distinct permutations. This is in contrast to combinations where the order of selection does not matter.
There are many different ways in which a set of objects can be arranged; hence we have a number of different types of permutations that are described below:
Types of Permutation
Permutation can be classified into the following different types:
- Permutation where repetition is not allowed.
- Permutation where repetition is allowed.
- Permutation of objects that are non-distinct.
- Circular permutations.
- $P(n,r)$ represents permutations for $n$ different objects taken $r$ at a time, and we have derived its formula in the last section. This applies when we have $n$ different objects to arrange, and repetition is not allowed.
- A permutation is easiest to calculate when repetition is allowed. Here we have $n$ objects, and $r$ represents a selection of the objects, but unlike when repetition is not allowed, in this case, we can select an object in $n$ different ways during each selection. So, we get $n \times n \times n \times n \times \cdots r \,\,\textrm{times}= n^{r}$
Let us first study examples related to these two types
Example 4: How many 4 letters words can be formed out of the letters of the word “Cables” when repetition is not allowed?
Solution:
The word “Cables” has five letters so $n=6$ and we have to form all possible four-letter words without repetition hence $r = 4$. Therefore, possible permutations can be calculated as:
$ P(n,r) = \frac{n!}{(n-r)!} $
$ P(5,3)=\frac{6!}{(6-4)!} $
$ P(5,3)=\frac{6 \times5 \times4 \times3 \times2 \times1}{(2\times1)}$
$ P(5,3)=360$
Example 5: How many $4$ letter words can be formed out of the letters of the word “Cables” when repetition is allowed?
Solution:
Permutation in the case of repetition is calculated in exponential form. If the number of objects is $n$ and the number $r$ is to be selected from $n$ objects, and if repetition is allowed, then permutation is expressed as $n^r$.
So, in the current example, the number of letters are six so $n=6$ while $r =4$
Permutation $ = 6 ^ {4} $
$ = 1296 $
Example 6: How many signals can be given by $6$ lights of different colors while using $3$ lights at a same time?
Solution:
Total number of lights $ = 6 $
Number of used lights $ = 3 $
$P(6,3)=\frac{6!}{(6-3)!} $
$P(6,3)=\frac{6 \times5 \times 4 \times3 \times2 \times1}{(3 \times2 \times1)}$
$P(6,3)=210 $
Example 7: How many 4-digits number can be formed by using the digits $3,4,5,6,7,8,9$ only once?
Solution:
Total number of digits $ = 7 $
Number of used lights $ = 4 $
$P(7,4)=\frac{7!}{(7-4)!}$
$P(5,3)=\frac{7 \times6 \times5\times4 \times3 \times2 \times1}{(3 \times2 \times1)}$
$P(5,3)=840 $
Example 8: How many six-digit numbers can be formed by using the digits $1, 2,5,6,7$ and $8$ but with the condition.
- The digits $5$ and $8$ are next to each other
- The digits $5$ and $8$ are not next to each other
Solution:
1) We have to calculate 6-digit numbers where digits 5 and 8 are next to each other. So, there are two possibilities, 58 and 85.
Let $(5, 8)$ be a single-digit
Now total numbers of digits are $1, 2, 58, 6, 7$ or $1, 2, 6, 7, 85$
So, Permutations containing digit $(58) = P(5,5) = \frac{5!}{(5-5)!}= 5!$
= $ 5 \times 4 \times 3 \times 2 \times 1 = 120$
Permutations containing digit $(85) = P(5,5) = 5!$
$= 5 \times 4 \times 3 \times 2 \times 1 = 120$
Hence total number of permutations in which $8$ and $5$ are next to each other = $120+120 = 240$.
2) There are total no. of six digits so permutations for $6$ digits is given as
$ = P(6,6) = \frac{6!}{(6-6)!}= 6!$
$ = 720$
So by subtracting the permutation containing digit $(5, 8)$ together, we will get the answer for this part.
Total numbers in which digit $5$ and $8$ are together $= 120$
Total numbers in which digit $5$ and $8$ are not together $ = 720-120 = 600$
Example 9: How many words can be formed by using all the letters of different words given below? (Repetition of words is not allowed).
- ENGLAND
- PENCIL
- NEST
Solution:
1.Permutations for the word ENGLAND by using all letters at same time will be
$P(7,7) = \frac{7!}{(7-7)!}$
$ = \frac{7!}{(0)!}$
$ = \frac{7 \times 6 \times5 \times4 \times3 \times2 \times1}{1}$
$ = 5040$
2. Permutations for the word PENCIL by using all letters at same time will be
$P(6,6) = \frac{6!}{(6-6)!}$
$ = \frac{6!}{(0)!}$
$ = \frac{6 \times5\times4\times3\times2\times1}{1}$
$ = 720$
3.Permutations for the word NEST by using all letters at same time will be
$P(4,4) = \frac{4!}{(4-4)!}$
$ = \frac{4!}{(0)!}$
$ = \frac{4\times3 \times2 \times1}{1}$
$ = 24$
Permutation of Non-distinct Objects
So far, we have studied the permutation of distinct objects. What if we are given a set of non-distinct objects, i.e., a set in which elements are repeated.
How do we solve permutation problems if the objects cannot be distinguished?
Suppose we have to find permutations of $n$ objects, and not all the n objects are distinct. Some of the objects repeat themselves or are lookalike. Let $Z$ be the required number of permutations, and it contains $n$ objects, and out of those $n$ objects $n1$ are all alike, $n2$ are alike of a second kind, and $n3$ are alike of a third kind.
So, the $n1$ lookalike objects will be permuted among themselves while $n2$ lookalike objects will be permutated among themselves, and similarly, $n3$ lookalike objects will be permuted among themselves. Hence the permutation of $n$ different objects will be the product of $Z \times n1! \times n2! \times n3 != n!$. Hence,
$\large{Z = \frac{n!}{n1! \times n2! \times n3!}}$
Suppose you are given four similar cups and 3 similar plates, and you are required to arrange them in a cupboard with 7 slots. Unlike previous examples where the $n$ number of given objects was different. Here, we have four similar cups and 3 similar plates.
Four similar cups can be arranged in any manner, but as they are similar, they will be permutated among themselves, i.e., $4!= 24$ while the three similar plates will be permutated among themselves $3!=6$. Both these redundant elements are then divided from the total number of possible permutations to get the required number of permutations.
Total number of permutations $ = \frac{7!}{(4!)(3!)}$
$ = \frac{5040}{144}$
$ = 35$
Let us take another example; we have to find the permutation of letters of the word $\textrm{“GOOD”}$. The word $\textrm{“GOOD”}$ consists of four letters, so $n=4$. As we can see, all the letters of the word $\textrm{“GOOD”}$ are not different, and it has 2 O’s in it, so, $n1=2$. We name the O’s as “O1” and “O2”. If we replace the O’s with “O1” and “O2.”
$\textrm{“GO1O2D”, “GO2O1D”}$
These are the two permutations of the word $\textrm{“GOOD”}$ if we replace the O’s with O1 and O2. Similarly, the replacement of these O’s in any other permutation of the word will give rise to two permutations of O’s. These redundant permutations are then divided from the total number of permutations to get the required answer.
Hence permutations of the word $\textrm{“GOOD”}$, if all words are taken at same time can be given as
$ = \frac{5!}{2!}$
$ = \frac{4 \times 3 \times 2 \times 1}{2}$
$ = 12$
Example 10: How many words can be formed by using all the letters of different words given below?
- MISSISSIPPI
- BANANA
- MATHEMATICS
Solution:
1) To find the permutations for the word $\textrm{MISSISSIPPI}$ by using all letters at the same time, we note that $n= 11$.
The letter $I$ repeats four times so $n1= 4$.
The Letter $S$ repeats four times so $n2 = 4$.
The letter $P$ repeats two times so $n3= 2$.
The letter $M$ only comes once so $n4 =1$.
Hence the required number of permutations is
$ = \frac{11!}{(4)! \times(4)! \times(2)! \times(1)!}$
$ = \frac{39916800}{1152}$
$ = 34650$
2) To find the permutations for the word $\textrm{BANANA }$by using all letters at the same time, we note that $n= 6$.
The letter $A$ repeats four times so $n1= 3$.
The Letter $N$ repeats four times so $n2= 2$.
The letter $B$ only comes once so $n3=1$.
Hence the required number of permutations is
$ = \frac{6!}{(3)!\times(2)!\times(1)!}$
$ = \frac{720}{12}$
$ = 60$
3) To find the permutations for the word $\textrm{MATHEMATICS}$ by using all letters at the same time, we note that $n= 11$.
The letter $M$ repeats four times so $n1= 2$.
The Letter $T$ repeats four times so $n2= 2$.
The letter $A$ repeats two times so $n3= 2$.
The rest of the letters only comes once.
Hence the required number of permutations is
$= \frac{11!}{(2)!\times(2)!\times(2)!}$
$= \frac{39916800}{8}$
$= 49896800$
Example 11: How many permutations of the word $\textrm{ASSASSINATION}$ can be formed if all the possible arrangements start with the letter $N$ and end with the letter $T$.
Solution:
As the letter “O” is fixed at the start and the letter “T” is fixed at the end, so we have to find the permutation for the remaining letters, which in total are 11
Here $n= 11$
The letter $S$ repeats four times so $n1= 4$.
The Letter $A$ repeats four times so $n2= 3$.
The letter $I$ repeats two times so $n3= 2$.
The letter $N$ repeats two times so $n4= 2$.
Hence the required number of permutations is
$ = \frac{11!}{(4)!\times(3)!\times(2)!\times(2)!}$
$ = \frac{39916800}{576}$
$ = 69300$
Example 12: How many numbers greater than $5000$ can be formed from the digits $1,5,5,5$? Repeat the same question when the digits are $6,5,5,7$.
Solution:
The required number should be greater than $5000$, and the digits we have are $1, 5, 5, 5$. The number cannot start with the digit $1$. The number can only be formed with the digit $5$ at the start.
$5$ __ __ __
With $5$ at the start the remaining digits are three so $n= 3$ while digit $5$ repeats itself 2 times so $n1= 2$ and the digit $1$ comes only once so $n2=1$
$= \frac{3!}{(2)!\times 1}$
$= \frac{6}{2}$
$= 3$
The required number greater than $5000$ with digits $6,5,5,7 $can be calculated as
$ 5$ __ __ __
$ = \frac{3!}{1}$
$ = \frac{6}{1}$
$ = 6$
$ 6$ __ __ __
$= \frac{3!}{2!}$
$= \frac{6}{2}$
$= 3$
$7$ __ __ __
$= \frac{3!}{2!}$
$= \frac{6}{2}$
$= 3$
So adding all of them, we get the required number = $6+3+3$
= $12$
Circular Permutations
All previous examples are related to linear problems and can be represented on points in a straight line. The permutation of objects which can be represented in a circular form is called a circular permutation. Let us take an example of $8$ people sitting at a round table.
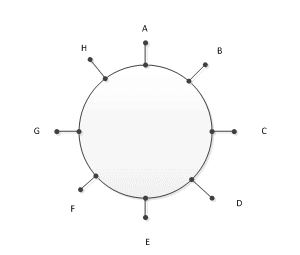
$\textrm{A, B, C, D, E, F, G, and H }$are $8$ persons sitting at a round table. In how many ways these $8$ people can be seated at a round table? As this is a round table and even if we move each person to left or right, they will be occupying different seats, but their position relative to another person will still remain the same.
So when person $\textrm{“A”}$ sits on the first seats, the rest of the persons will be permuting among the remaining seats. In this example, if $\textrm{“A”}$ acquires the first seat, so the remaining persons are 7, and hence the total number of arrangements will be $7! = 5040\, ways$
Example 13: A king calls the meeting of 5 knights? The meeting is to be held at a round table. Tell the total number of possible arrangements in which they (Including the king) can be seated at the round table.
Solution:
If we include the king, the total numbers of person are six. King gets the first seat, so the total remaining knights are $5$, so the total numbers of possible arrangements are $5! = 120$
Practice Questions:
- How many numbers greater than 57000 can be formed from the digits 5, 6,7,8,9 without repeating any digit?
- Find the number of ways in which 5 men and 4 women can be seated in a row such that.
- If there are no restrictions
- Two men sit next to each other
- Two women do not sit next to each other
- How many permutations of the word “PASSPORT” can be formed if all the possible arrangements start with the letter “R”?
- How many six-digit numbers will lie between 500,000 and 580,000 by using the digits 3, 3, 5,5,8,8?
- In how many ways 6 men and 5 women can be seated on a couch when both are occupying alternative seats?
Answer Key
1)
Numbers greater than $57000$ can be formed as
$58$ __ __ __ $= (P3,3) = 3! = 6$
$59$ __ __ __ $= P(3,3 ) = 3! = 6$
$6$ __ __ __ __ $= P(4,4) = 4! = 24$
$7$ __ __ __ __ $= P(4,4) = 4! = 24$
$8$ __ __ __ __ $= P(4,4) = 4! = 24$
$9$ __ __ __ __ $= P(4,4) = 4! = 24$
Total required numbers $= 6+6+24+24+24+24 = 108$
2)
The number of men is $5$, and the number of women are $4$, so; we have a total number of $9$ persons.
- In this first case, as there are no restrictions so, we are arranging $9$ persons in a row, and the total number of possible arrangements will be $9! = 362880$
- In this case, two men have to sit next to each other. If we take these two men as a single entity, then the remaining arrangements can be made in $8! = 40320$ ways, and as the men have to sit together, so their possible arrangement is $2!= 2$. So, the total number of possible arrangements is $8! \times 2! = 80640$ ways.
- In this case, two women should not sit together. As we have calculated in (b) part, the possible number of ways the two women can sit together will be $40320$, and if we subtract that from the total number of possible arrangements, we will get the arrangement where two women cannot sit together. Hence, required number of arrangements $= 362880 – 40320 = 322560$.
3)
Letter “R” is fixed at start
$n= 7$
$n1= 2$ (P)
$n2= 2$ (S)
$ = \frac{7!}{(2)! \times (2)!}$
$ = \frac{5040}{4}$
$ = 1260$
4)
The numbers lying between 500,000 and 580,000 are of the form
$53$ __ __ __ __
So $n=4$ while $n1 =2$ and the rest are single digit
$ = \frac{4!}{2!} = 12$
$55$__ __ __ __
So $n=4$ while $n1 =2$ and $n2=2$
$ = \frac{4!}{(2!)\times (2)!} = 6$
Total number of required numbers are $ = 12+6 = $18$
5)
Suppose “M” is for men and “W” is for women
Seat arrangements will be MWMWMWMWMWM $ = P(6,6) \times P(5,5)$
$= 6! \times 5! $
$ = 720 \times 120$
$ = 86400$
