Polar to rectangular equation – Equations, Graphs, and Examples

We can convert polar equations to rectangular form to rewrite a rectangular equation in terms of $x$ and $y$ to an equation of the form $r$ and $\theta$. Knowing how to convert equations to rectangular and polar forms will help observe multiple relationships between two sets of data.

Converting polar to rectangular equation will require us to use the relationship between $\boldsymbol{x}$ and $\boldsymbol{\cos \theta}$ as well as $\boldsymbol{y}$ and $\boldsymbol{\sin \theta}$.

This article focuses on learning how we can rewrite a polar equation in its rectangular form. To make the most out of our discussion, make sure to take a refresher on the following topics:

• Understanding how we can express trigonometric ratios in terms of $x$, $y$, and $r$.
• Manipulating trigonometric expressions using trigonometric identities.
• Learning how to convert coordinates in rectangular and polar form.

For now, we can refresh our knowledge on converting polar coordinates to rectangular coordinates and see how we can extend this to converting polar equations.

How to convert polar equation to rectangular form?                

Recall that we can convert a polar coordinate, $(r, \theta)$, to its rectangular form using the properties shown below.

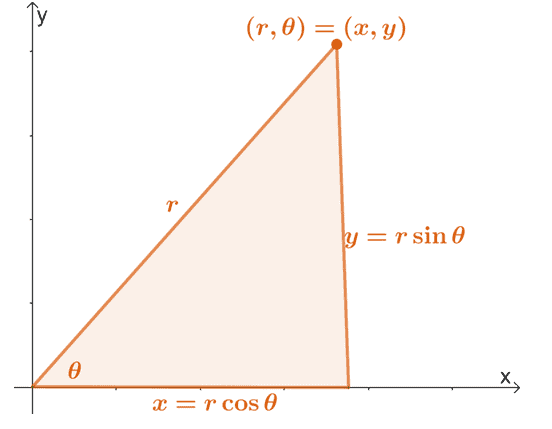
We can extend this properties to find the expressions of $r$ and $\theta$ in terms of $x$ and $y$. Hence, we have the following equations:

\begin{aligned}x&= r\cos \theta\\y&= r\sin \theta\\\\r^2 &= x^2 + y^2\\\tan \theta &= \dfrac{y}{x}\end{aligned}

This means that whenever we’re given a polar equation, we can convert it to rectangular form by using any of the four equations shown above.

• Rewrite the polar equation so that it’s in terms of $r\cos \theta$, $r\sin \theta$, and $\tan \theta$.
• Replace the polar expressions with their rectangular equivalent.
• Simplify the resulting equation whenever necessary.

For, example, if we want to change $r = 2\csc \theta$ in its rectangular for, we’ll need to rewrite $2\csc \theta$ in terms of $\sin \theta$. Recall that $\csc \theta = \dfrac{1}{\sin \theta}$, so let’s use this reciprocal identity to rewrite the expression.

\begin{aligned}r  &= 2\csc \theta \\r&= 2\cdot \dfrac{1}{\sin \theta}\end{aligned}

We can multiply both sides of the equation by $\sin \theta$ then replace $r\sin \theta$ with its rectangular form, $y$.

\begin{aligned}r \color{blue}{\cdot \sin \theta}&= 2\cdot \dfrac{1}{\sin \theta}\color{blue}{\cdot \sin \theta}\\ r\sin \theta &= 2\\y &= 2\end{aligned}

This means that the rectangular form of $r = 2\csc \theta$ is $y = 2$. This equation represents a horizontal line that passes through the point, $(0, 2)$.

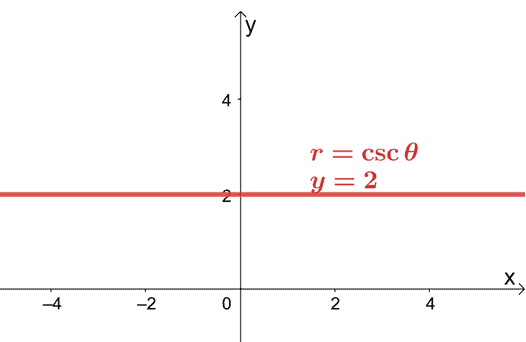
This shows that it’s still possible to graph a polar equation on an $xy$-coordinate system by converting the polar equation to its rectangular form.

Converting polar equations to rectangular to graph the resulting equation

As we have mentioned in the earlier section, we graph polar equations on a rectangular coordinate system by rewriting the polar equations to their rectangular form first.

• Rewrite the equation in terms of $x$ and $y$ using the four equations we’ve discussed.
• Identify the parent function that the equation represents to have an idea of the best approach to graph the equation.
• Assign key values for $(x, y)$ to help as guides when graphing the rectangular equation.

 Let’s say we want to graph $\tan \theta = 4$ on the $xy$-plane. We can replace $\tan \theta$ with $\dfrac{y}{x}$ and convert the polar equation to its rectangular form.

\begin{aligned}\tan \theta &= 4\\\dfrac{y}{x} &= 4\\y &= 4x\end{aligned}

The equation, $y = 4x$, is a linear equation, so we can use $(-2, -8)$ and $(2, 8)$ to guide us  in graphing the $y = 4x$ as shown below.

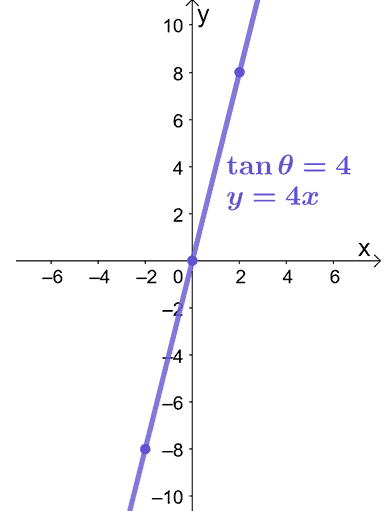
That’s all we need to graph a polar equation on a rectangular coordinate system. Are you ready to try out more problems? Don’t worry; we’ve prepared more sample problems for you to work on!

Example 1

Convert the polar equation, $r = -6\sec \theta$ as a rectangular equation. Graph the resulting equation on an $xy$-coordinate system.

Solution

We can rewrite $\sec \theta$ in terms of cosine using the reciprocal identity, $\sec \theta = \dfrac{1}{\cos \theta}$. Let’s rewrite the polar equation as shown below.

\begin{aligned}r&=-6 \sec \theta \\r&= -6 \cdot\dfrac{1}{\cos \theta} \end{aligned}

We can then multiply both sides of the equation by $\cos \theta$. Replace the left-hand side of the equation with the rectangular equivalent of $r \cos \theta$.

\begin{aligned}r \color{blue}{\cdot \cos \theta}&= -6 \cdot\dfrac{1}{\cos \theta}\color{blue}{\cdot \cos \theta}\\r \cos \theta &= -6\\x &= -6 \end{aligned}

This means that the polar form of $r = -6\sec \theta$ is equal to $x = -6$. We can see that the equation $x = -6$ is a vertical linear function that passes through the point $(-6, 0)$.

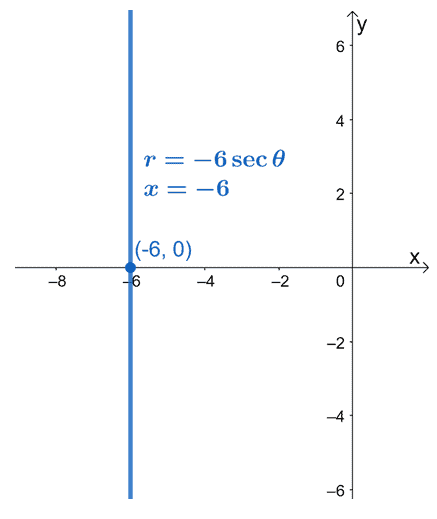
Example 2

Convert the following polar equations to their rectangular forms. Make sure that the resulting rectangular equation is in its standard form.

1. $r = 4 \cos \theta$
2. $r = -6 \sin \theta$

Solution

The two equations will have to be manipulated so that they represent any of the four equations shown below.

\begin{aligned}x&= r\cos \theta\\y&= r\sin \theta\\\\r^2 &= x^2 + y^2\\\tan \theta &= \dfrac{y}{x}\end{aligned}

The easiest approach is for us to multiply both sides of the equation by $r$, so we end up with $r^2$ on the right-hand side of the equation.

\begin{aligned}r&=2 \cos \theta\\r \color{blue}{\cdot r} &= (2 \cos \theta)\color{blue}{\cdot r}\\r^2 &= 2r\cos \theta \end{aligned}

Notice two expressions we can convert to their polar forms? We can rewrite $r^2$ as $x^2 + y^2$ and $r \cos \theta$ as $x$.

\begin{aligned}\color{blue}{r^2 }&= 4\color{blue}(r\cos \theta)\\\color{blue}{x^2 + y^2} &= 4 {\color{blue}x} \\x^2 + y^2 &= 4x\end{aligned}

We can transpose $4x$ to the left-hand side of the equation then complete the square for $x^2 – 4x$. We can then factor the perfect square trinomial to end up with an equation we’re familiar with.

\begin{aligned}x^2 -4x + y^2 &= 0\\ (x^2 – 4x {\color{blue} +  4}) + y^2 &= 0 {\color{blue} +  4}\\(x^2 – 4x + 4)+ y^2 &= 4\\(x-2)^2 + y^2 &= 4\end{aligned}

This shows that the rectangular form of $r = 4 \cos \theta$ is equivalent to $(x – 2)^2 + y^2 = 4$, which is the equation of a circle centered at $(2, 0)$ and a radius of $2$ units.

We’ll apply a similar process to convert $r = -6 \sin \theta$ to its rectangular form:

• Multiply both sides of the equation by $r$.
• Replace $r^2$ and $r\sin \theta$ with $x^2 + y^2$ and $y$, respectively.

\begin{aligned}r&=-6 \sin \theta \\r {\color{green}\cdot r}&=-6 {\color{green} r}\sin \theta\\r^2 &=-6r\sin\theta\\ {\color{green}x^2 + y^2} &= -6({\color{green}y})\\x^2 + y^2 &= -6y\end{aligned}

We can then rearrange the equation and come up with a rectangular equation in rectangular form.

• Move $-6y$ on the left-hand side of the equation.
• Complete the perfect square for $y^2 + 6y$.
• Express $y^2 + 6y + 9$ as a perfect square.

\begin{aligned}x^2 + y^2 + 6y &=0\\x^2 +  (y^2 +6y {\color{green} + 9} )&= {\color{green} 9}\\x^2 + (y +3)^2 &= 9 \end{aligned}

This means that $r = -6 \sin \theta$ is equivalent to $x^2 + (y+ 3)^2 =9$ in rectangular form.

Example 3

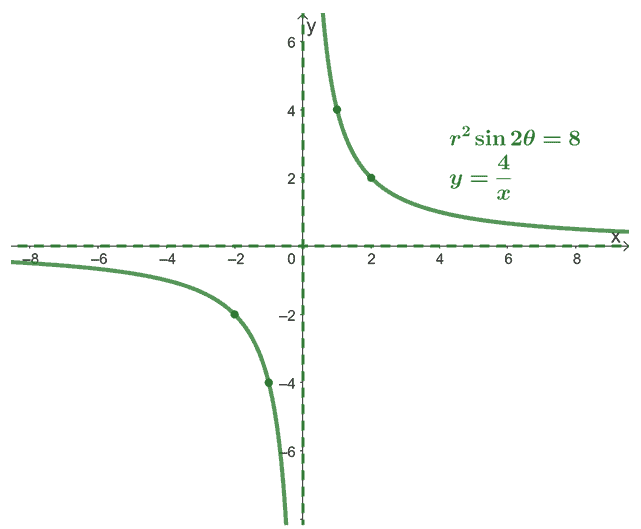
Convert the polar equation, $r^2 \sin 2\theta = 8$ as a rectangular equation. Graph the resulting equation on an $xy$-coordinate system.

Solution

We have no direct conversion for $\sin 2\theta$ if we want to convert the equation in rectangular form. Instead, what we can do is express $\sin 2\theta$ in terms of $\cos \theta$ and $\sin \theta$ using the double-angle identity for sine as shown below.

\begin{aligned}r^2 {\color{green}(\sin 2\theta) }&= 8\\r^2 {\color{green}(2\sin \theta \cos \theta) }&= 8 \end{aligned}

We can then distribute $r^2 = r\cdot r$ to $\cos \theta$ and $\sin \theta$. Let’s rearrange the equation and end up with $r \cos theta$ and $r\sin \theta$ on the left-hand side of the equation.

\begin{aligned}(r \cdot r)(2\sin \theta \cos \theta)&= 8\\2(r\cos \theta)(r\sin \theta)&= 8\\\dfrac{2(r\cos \theta)(r\sin \theta)}{2}&= \dfrac{8}{2}\\(r \cos \theta)(r \sin \theta) &= 4 \end{aligned}

We now have polar expressions we can replace with their rectangular forms, so let’s replace $r\cos \theta$ and $r\sin \theta$ with $x$ and $y$, respectively. Isolate $y$ on the left-hand side of the equation to write the equation in standard form.

\begin{aligned}({\color{blue}r \cos \theta})({\color{blue}r \sin \theta}) &= 4\\({\color{blue}x})({\color{blue}y}) &= 4\\xy&=4\\y&= \dfrac{4}{x} \end{aligned}

This means that when converted to a rectangular equation, $r^2 \sin 2\theta = 6$, is equivalent to the reciprocal function, $y = \dfrac{4}{x}$.

The value of $x$ can never be zero, so we’re expecting $x = 0$ and $y =0$ to be asymptotes. Let’s assign some values for $x$ to find some points for $(x, y)$.

We can graph these points as a guide to graph the reciprocal function, $y=\dfrac{4}{x}$.

This shows that we can convert polar equations to rectangular equations and graph them using our past knowledge of functions.