- Home
- >
- Power reducing identities – Formulas, Proof, and Application
Power Reducing Identities – Formulas, Proof, and Application
 Power-reducing identities help us in rewriting different trigonometric functions that a power has raised. They will come in handy, especially when we want to evaluate complex trigonometric functions and equations. They will definitely come in handy in your Calculus classes.
Power-reducing identities help us in rewriting different trigonometric functions that a power has raised. They will come in handy, especially when we want to evaluate complex trigonometric functions and equations. They will definitely come in handy in your Calculus classes.
Power reducing identities are trigonometric identities that allow us to rewrite trigonometric expressions that are raised to a power in terms of simpler trigonometric expressions.
In this article, we’ll learn how to derive these identities, apply them to prove other trigonometric identities, and extend our knowledge by answering other problems that involve trigonometric expressions.
To make the most out of this article, make sure to refresh your knowledge on trigonometric identities, double-angle formulas, half-angle formulas, and trigonometric equations. For now, let’s understand the three main power reducing identities that we need the most.
What are power reducing identities?
As we have mentioned in the earlier section, we use power reducing identities to rewrite trigonometric expressions raised by a certain expression with simpler terms. Once the expression has simpler terms, it may be easier for us to apply other trigonometric properties and identities.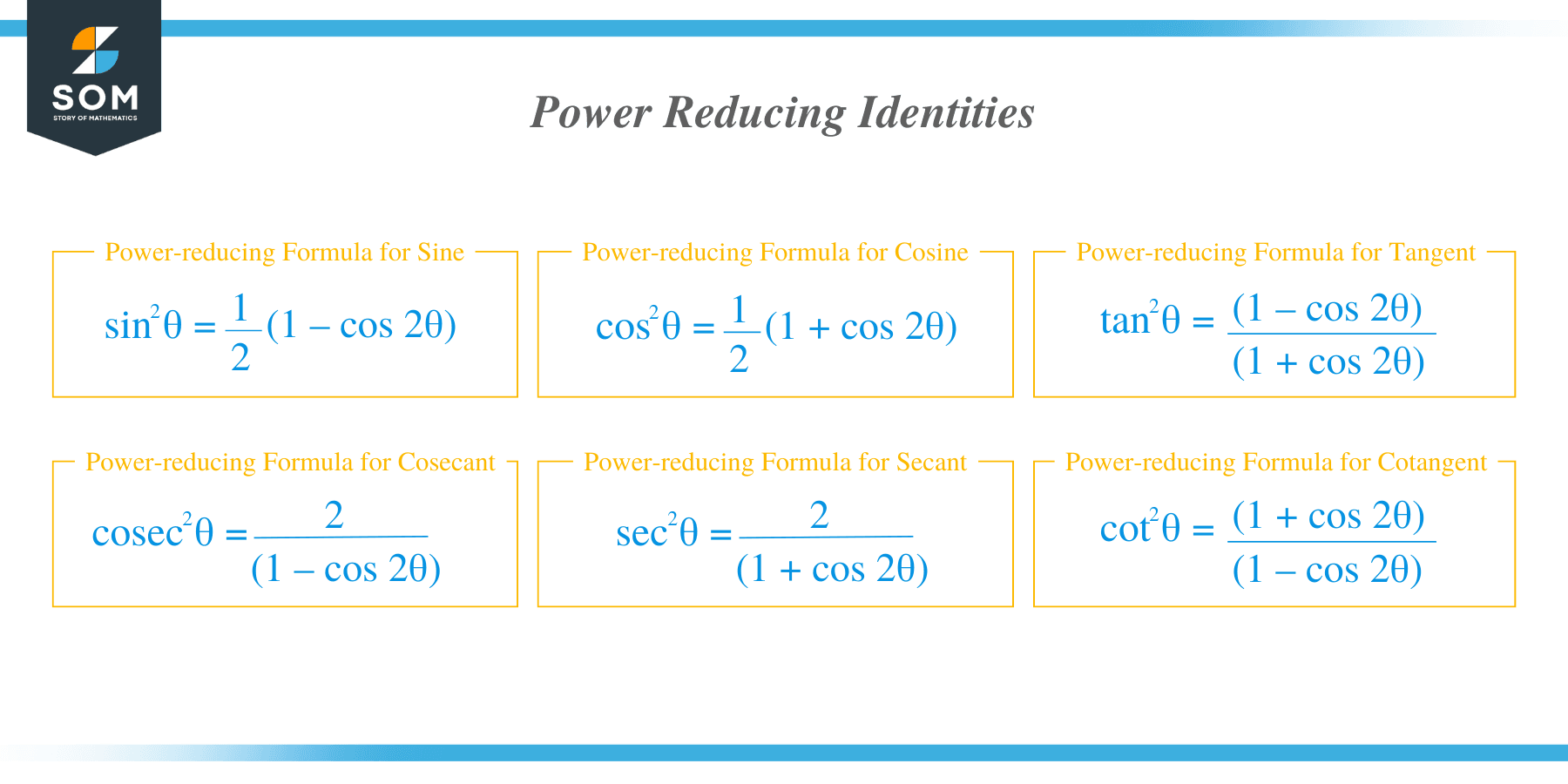
Power-reducing Formula for Sine | $\sin^2\theta = \dfrac{1}{2}(1 – \cos \theta)$ |
Power-reducing Formula for Cosine | $\cos^2\theta = \dfrac{1}{2} (1+ \cos 2\theta)$ |
Power-reducing Formula for Tangent | $\tan^2\theta = \dfrac{1- \cos 2\theta}{1+ \cos 2\theta}$ |
How to derive the power reduction formula?
These power reducing identities can be derived from the double-angle and half-angle identities. Let’s begin by recalling the double-angle formulas for sine and cosine.
\begin{aligned}\cos(2\theta) &= \cos^2\theta -\sin^2 \theta \phantom{xxx} \end{aligned}
We can obtain the power-reducing formula for cosine by isolating the $\cos^2 \theta$ on the equation’s left-hand side.
\begin{aligned}\cos(2\theta) &= \cos^2\theta -\sin^2 \theta\\ \cos^2\theta &=\cos (2\theta) + \sin^2 \theta\end{aligned}
Using the Pythagorean identity, $\cos^2 \theta + \sin^2 \theta= 1$, we can rewrite the right-hand side of the equation.
\begin{aligned}\cos^2\theta &=\cos (2\theta) + (1+\cos^2 \theta)\\2\cos^2\theta &= 1+ \cos 2\theta\\\cos^2\theta &= \dfrac{1}{2} (1+ \cos 2\theta)\end{aligned}
Hence, we have the power-reducing formula for cosine, $\cos^2\theta = \dfrac{1}{2} (1+ \cos 2\theta)$.
We can apply a similar process to derive the power-reducing formula for sine.
\begin{aligned}\cos(2\theta) &= \cos^2\theta -\sin^2 \theta\\ \sin^2\theta &=\cos^2 \theta – \cos (2\theta) \\\sin^2 \theta &= (1- \sin^2 \theta) – \cos 2\theta\\2\sin^2\theta&= 1 – \cos 2\theta\\\sin^2\theta &= \dfrac{1}{2}(1 – \cos \theta)\end{aligned}
We just derived the power-reducing formula for sine: $\sin^2\theta = \dfrac{1}{2}(1 – \cos \theta)$.
To derive the power-reducing formula for the tangent, we divide $\sin^2 \theta$ by $\cos^2 \theta$.
\begin{aligned}\tan^2 \theta &= \dfrac{\sin ^2 \theta}{\cos^2\ \theta}\\&= \dfrac{\dfrac{1}{2}(1 – \cos \theta)}{\dfrac{1}{2} (1+ \cos 2\theta)}\\&=\dfrac{1 – \cos \theta}{1 + \cos \theta} \end{aligned}
This proves the third power-reducing identity, $\tan^2 \theta = \dfrac{1 – \cos \theta}{1 + \cos \theta}$.
We’ve just shown how we can derive the three power-reducing identities using a double-angle formula. It’s also possible for us to actually verify this identity using the half-angle identity. Let’s go ahead and master the three identities by solving the problems shown below.
Example 1
Verify the power-reducing formulas using the half-angle identities.
Solution
As we have mentioned, we can also prove the three power-reducing identities by using the half-angle identities. We can begin by recalling what three half-angle identities are:
\begin{aligned}\cos \dfrac{\alpha}{2} &= \pm \sqrt{\dfrac{1}{2}(1 + \cos \alpha)}\\\sin \dfrac{\alpha}{2} &= \pm \sqrt{\dfrac{1}{2}(1 – \cos \alpha)}\\\tan \dfrac{\alpha}{2}&=\pm \sqrt{\dfrac{1 – \cos\alpha}{1 + \cos \alpha}}\end{aligned}
What we can do is simply square both sides of the equation for all three identities.
\begin{aligned}\left( \cos \dfrac{\alpha}{2}\right )^2 &= \left( \pm \sqrt{\dfrac{1}{2}(1 + \cos \alpha)}\right )^2\\\cos^2 \dfrac{\alpha}{2} &=\dfrac{1}{2}(1 + \cos \alpha)\end{aligned} | \begin{aligned}\left( \sin \dfrac{\alpha}{2}\right )^2 &= \left( \pm \sqrt{\dfrac{1}{2}(1 – \cos \alpha)}\right )^2\\\sin^2 \dfrac{\alpha}{2} &=\dfrac{1}{2}(1 – \cos \alpha)\end{aligned} | \begin{aligned}\left( \tan\dfrac{\alpha}{2}\right )^2 &= \left( \pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}}\right )^2\\\tan^2 \dfrac{\alpha}{2} &=\dfrac{1-\cos \alpha}{1+\cos \alpha}\end{aligned} |
Let’s say $\alpha$ represents $2\theta$, we can rewrite the three identities in terms of $\theta$.
\begin{aligned}\cos^2 \dfrac{2\theta}{2} &=\dfrac{1}{2}(1 + \cos 2\theta)\\\cos^ 2\theta &= \dfrac{1 + \cos 2\theta }{2}\end{aligned} | \begin{aligned}\sin^2 \dfrac{2\theta}{2} &=\dfrac{1}{2}(1 – \cos 2\theta)\\\sin^ 2\theta &= \dfrac{1 – \cos 2\theta }{2}\end{aligned}\begin{aligned}\tan^2 \dfrac{2\theta}{2} &=\dfrac{1-\cos 2\theta}{1+\cos 2\theta}\\\tan^2 \theta &=\dfrac{1-\cos 2\theta}{1+\cos 2\theta}\end{aligned} | \begin{aligned}\tan^2 \dfrac{2\theta}{2} &=\dfrac{1-\cos 2\theta}{1+\cos 2\theta}\\\tan^2 \theta &=\dfrac{1-\cos 2\theta}{1+\cos 2\theta}\end{aligned} |
Hence, we’ve also verified the three power-reducing formulas using the three half-angle identities.
Example 2
Apply the appropriate power reduction identity to rewrite $\sin^4 \theta$ in terms of $\sin \theta$ and $\cos \theta$ (and both must only have the first power).
Solution
We can rewrite $\sin^4 \theta$ as the square of $\sin^2 \theta$. We can then use the power reduction formula, $\sin^2\theta = \dfrac{1}{2}(1 – \cos \theta)$.
\begin{aligned}\sin^4 \theta &= (\sin^2 \theta)^2\\&=\left(\dfrac{1 – \cos 2\theta}{2} \right )^2\end{aligned}
Let’s expand the right-hand side of the equation and use the algebraic property, $(a +b)^2 = a^2 + 2ab + b^2$, to rewrite the numerator.
\begin{aligned}\sin^4 \theta &=\dfrac{(1 – \cos 2\theta)^2}{2^2}\\&=\dfrac{1^2 – 2(1)(\cos 2\theta)+ (\cos 2\theta)^2}{4}\\&= \dfrac{1 – 2 \cos 2\theta + \cos^2 2\theta}{4}\end{aligned}
At this point, we only have one term that needs rewriting – $(\cos^2 2\theta)$. We can apply the power reduction formula, $\cos^2\theta = \dfrac{1}{2}(1 + \cos \theta)$, to rewrite this term so that $\cos \theta$ is only in the first power. Manipulate the expression after to simplify the right-hand side of the equation further.
\begin{aligned}\sin^4 \theta &= \dfrac{1 – 2 \cos 2\theta + \dfrac{1}{2}[1 + \cos(2\cdot 2\theta)]}{4}\\&=\dfrac{\dfrac{1}{2}(2 – 4\cos 2\theta + 1+ \cos 4\theta)}{4}\\&=\dfrac{1}{8}(3-4\cos 2\theta + \cos 4\theta)\\&= \dfrac{3}{8}-\dfrac{1}{2}\cos 2\theta+ \dfrac{1}{8}\cos 4\theta \end{aligned}
This means that $\sin^4 \theta = \dfrac{3}{8}-\dfrac{1}{2}\cos 2\theta+ \dfrac{1}{8}\cos 4\theta$. This new form has all sines and cosines written in the first power as we wanted it to be.
Example 3
Use any of the three power-reducing formulas to evaluate the following trigonometric expressions:
a. $\sin^2 15^{\circ}$
b. $\tan^2 22.5^{\circ}$
c. $\cos^2 \dfrac{\pi}{12}$
Solution
When working angles that return a special angle when multiplied by $2$, we can use the power-reducing formulas to evaluate them. Why don’t we write down the three formulas here to make it easier for us?
\begin{aligned}\sin^2\theta &= \dfrac{1}{2}(1 – \cos \theta)\\\cos^2\theta &= \dfrac{1}{2} (1+ \cos 2\theta)\\\tan^2\theta &= \dfrac{1- \cos 2\theta}{1+ \cos 2\theta}\end{aligned}
Notice that for each of the right-hand side, we have $\cos 2\theta$? That’s why this formula will work for the angles that we have.
Let’s begin with $\sin^2 15^{\circ}$ and use the first power-reducing power to rewrite $\sin^2 15$ in terms of cosine.
\begin{aligned}\sin^2 15^{\circ} &= \dfrac{1}{2}[1 – \cos (2\cdot15^{\circ})]\\&= \dfrac{1}{2}(1 – \cos 30^{\circ})\\&= \dfrac{1}{2} – \dfrac{1}{2}\cos 30^{\circ}\\&=\dfrac{1}{2}- \dfrac{1}{2}\cdot \dfrac{\sqrt{3}}{2}\\&=\dfrac{1}{2}- \dfrac{\sqrt{3}}{4} \end{aligned}
We can apply a similar process to evaluate $\tan^2 22.5^{\circ}$ using the power-reducing formula,$\tan^2\theta = \dfrac{1- \cos 2\theta}{1+ \cos 2\theta}$.
\begin{aligned}\tan^2 22.5^{\circ} &= \dfrac{1 – \cos(2\cdot 22.5^{\circ})}{1 + \cos(2\cdot 22.5^{\circ})}\\&= \dfrac{1 – \cos 45^{\circ}}{1 + \cos 45^{\circ}}\\&= \dfrac{1- \dfrac{\sqrt{2}}{2}}{1+ \dfrac{\sqrt{2}}{2}}\\&= \dfrac{1- \dfrac{\sqrt{2}}{2}}{1+ \dfrac{\sqrt{2}}{2}} \cdot \dfrac{2}{2}\\&= \dfrac{2- \sqrt{2}}{2+ \sqrt{2}} \end{aligned}
We can rationalize this value by multiplying both the numerator and denominator by the fraction’s conjugate, $2 – \sqrt{2}$.
\begin{aligned}\dfrac{2- \sqrt{2}}{2+ \sqrt{2}} &= \dfrac{2- \sqrt{2}}{2+ \sqrt{2}} \cdot \dfrac{2- \sqrt{2}}{2- \sqrt{2}}\\&= \dfrac{(2 -\sqrt{2})^2}{(2)^2 -(\sqrt{2})^2}\\&=\dfrac{2^2 – 2(2)\sqrt{2} + (\sqrt{2})^2}{4 – 2} \\&= \dfrac{6 – 4\sqrt{2}}{2}\\&=3 – 2\sqrt{2}\end{aligned}
We can apply the power-reducing formula for cosine to evaluate $\cos^2 \dfrac{\pi}{12}$ as shown below.
\begin{aligned}\cos^2 \dfrac{\pi}{12}&= \dfrac{1}{2}\left[1 + \cos \left(2\cdot \dfrac{\pi}{12}\right)\right]\\&= \dfrac{1}{2}\left(1 + \cos \dfrac{\pi}{6}\right)\\&= \dfrac{1}{2} + \dfrac{1}{2}\cos \dfrac{\pi}{6}\\&=\dfrac{1}{2}+ \dfrac{1}{2}\cdot \dfrac{\sqrt{3}}{2}\\&=\dfrac{1}{2}+ \dfrac{\sqrt{3}}{4} \end{aligned}
The three items have shown us that we can also use the three power-reducing formulas to evaluate and find a trigonometric expression’s exact value.
a. $\sin^2 15^{\circ} = \dfrac{1}{2} – \dfrac{\sqrt{3}}{4}$
b. $\tan^2 22.5^{\circ} = 3 – 2\sqrt{2}$
c. $\cos^2 \dfrac{\pi}{12} = \dfrac{1}{2}+ \dfrac{\sqrt{3}}{4}$
Example 4
Find the values of $\theta$ within the interval, $[0, 2\pi]$, that satisfy the equation,$\sin^2 \theta – \cos 2\theta = \dfrac{5}{4}$ .
Solution
It will be ideal to rewrite $\sin^2 \theta$ in terms of cosine in the first power since we have $\cos 2\theta$ as the second term on the left-hand side of the equation.
\begin{aligned}\sin^2 \theta – \cos 2\theta &= \dfrac{5}{4}\\\dfrac{1}{2}(1 – \cos 2\theta) – \cos 2\theta &= \dfrac{5}{4}\end{aligned}
Multiply both sides of the equation by $2$ and further simplify the left-hand side.
\begin{aligned}(1 – \cos 2\theta) – 2\cos 2\theta &= \dfrac{5}{2}\\1- 3\cos 2\theta&=\dfrac{5}{2} \\-3\cos 2\theta &=\dfrac{3}{2}\\\cos 2\theta &= -\dfrac{1}{2} \end{aligned}
Let’s now solve for $\theta$ and make sure that it is within the given interval, $[0, 2\pi]$.
\begin{aligned}2\theta &= \cos^{-1}\left(-\dfrac{1}{2}\right)\\2\theta &= \dfrac{2\pi}{3},\dfrac{4\pi}{3},\dfrac{8\pi}{3},\dfrac{10\pi}{3}\\\theta &= \dfrac{\pi}{3},\dfrac{2\pi}{3},\dfrac{4\pi}{3},\dfrac{5\pi}{3} \end{aligned}
Hence, the values of $\theta$ that satisfy the given equation are $\left\{\dfrac{\pi}{3},\dfrac{2\pi}{3},\dfrac{4\pi}{3},\dfrac{5\pi}{3}\right\}$.
Example 5
Verify the following trigonometric identities using the prove the following identities:
a. $2\cos^5 \alpha – 1 = \cos 10\alpha$
b. $ 2\cos 4\theta – 1 = 1- 8 \sin^2 \theta \cos^2 \theta$
Solution
The goal is to manipulate either the left or the right side of the equation so that both sides are equivalent.
We can use the power-reducing formula for cosine to rewrite the left-hand side of the first identity.
\begin{aligned}2\cos^5 \alpha -1 &= \cos 10\alpha\\2 \cdot \dfrac{1}{2}[1+ \cos 2(5\alpha)] – 1&= \cos 10 \end{aligned}
Simplify the left-hand side further until we end up with $\cos 10 \alpha$.
\begin{aligned}1 + \cos 2(5\alpha) – 1&=\cos 10\alpha\\\cos 10\alpha &= \cos 10\alpha \end{aligned}
As for the second identity, we can manipulate the right-hand side expression since we have both $\sin^2 \theta$ and $\cos^2 \theta$. We can apply the power-reducing formulas on the right-hand side of the identity.
\begin{aligned}\cos 4\theta &= 1- 8 \sin^2 \theta \cos^2 \theta\\&= 1- 8\left[\dfrac{1}{2}(1 – \cos 2\theta) \cdot \dfrac{1}{2}(1 + \cos 2\theta) \right ] \end{aligned}
Let’s factor out $\dfrac{1}{2}$ and apply the algebraic property, $(a – b)(a + b) = a^2 – b^2$, to rewrite the right-hand side.
\begin{aligned}\cos 4\theta &= 1 – 4[1^2 – (\cos 2\theta)^2]\\\cos 4\theta&= 1- 4(1 – \cos^2 2\theta)\\\cos 4\theta&=1- 4+ 4\cos^2 2\theta\\\cos 4\theta &= -3 + 4\cos^2 2\theta\end{aligned}
We can apply the power-reducing formula for cosine once more to rewrite $\cos^2 2\theta$.
\begin{aligned}\cos 4\theta &= -3 + 4 \left[\dfrac{1}{2}(1 + \cos 2\cdot 2\theta) \right ]\\\cos 4\theta &= -3 + 4\cdot\dfrac{1}{2} \left[(1 + \cos 2\cdot 2\theta) \right ]\\\cos 4\theta &= -3 + 2 + 2\cos 4\theta \\\cos 4\theta &= 2\cos 4\theta – 1\end{aligned}
Practice Questions
![]()
Open Problems
Verify the following trigonometric identities using the prove the following identities:
1. $\cos^2 2\alpha – \sin^2 2\alpha = \cos 4\alpha$
2. $\sin^2 \dfrac{\theta}{2} = \dfrac{\sec \theta – 1}{2 \sec \theta}$
Open Problem Solutions
1.
$\begin{aligned}\cos^2 2\alpha – \sin^2 2\alpha &= \cos 4\alpha\\\dfrac{1}{2}(1 + \cos 4\alpha)- \dfrac{1}{2}(1 – \cos 4\alpha)&= \cos 4\alpha\\\dfrac{1}{2} + \dfrac{1}{2}\cos 4\alpha- \dfrac{1}{2}-\dfrac{1}{2} \cos 4\alpha &= \cos 4\alpha\\\cos 4\alpha &=\cos 4\alpha \end{aligned}$
2.
$\begin{aligned}\sin^2 \dfrac{\theta}{2} &= \dfrac{\sec \theta – 1}{2 \sec \theta}\\\dfrac{1}{2}\left(1 – \cos 2\cdot \dfrac{\theta}{2} \right ) &= \dfrac{\sec \theta – 1}{2 \sec \theta}\\\dfrac{1}{2}\left(1 – \cos \theta \right ) &= \dfrac{\sec \theta – 1}{2 \sec \theta}\\\dfrac{\left(1 – \cos \theta \right )}{2} &= \dfrac{\sec \theta – 1}{2 \sec \theta}\\\dfrac{\left(1 – \cos \theta \right )}{2} \cdot \dfrac{\dfrac{1}{\cos \theta}}{\dfrac{1}{\cos \theta}} &= \dfrac{\sec \theta – 1}{2 \sec \theta}\\\dfrac{\dfrac{1}{\cos \theta} – 1}{2 \cdot \dfrac{1}{\cos \theta}} &= \dfrac{\sec \theta – 1}{2 \sec \theta}\\\dfrac{\sec \theta – 1}{2 \sec \theta}&= \dfrac{\sec \theta – 1}{2 \sec \theta} \end{aligned}$
