JUMP TO TOPIC
Probability of An Event – Explanation & Strategies
In the English language, the word event is used to refer to a special or desired occurrence. In probability, we use it in a similar way. Here is the definition:
In probability, we define an event as a specific outcome, or a set of specific outcomes, of a random experiment.
In this article we will further explore:
- What is meant by an event in probability
- Types of Events
- How to find the probability of an event
Once we have gone through the concepts and tried some examples, you will be better able to try the questions at the end. Let’s begin!
What is an event in probability?
In probability, we are interested in the chances of a particular event taking place. For example, getting an even number when you roll a die, or getting a head when you toss a coin. The outcome of getting an even number is considered an event. The outcome of getting a head is also considered an event. How then do we define the term event as used in this context?
Event Definition in Probability
An event is a specific outcome, or a set of specific outcomes, of a random experiment.
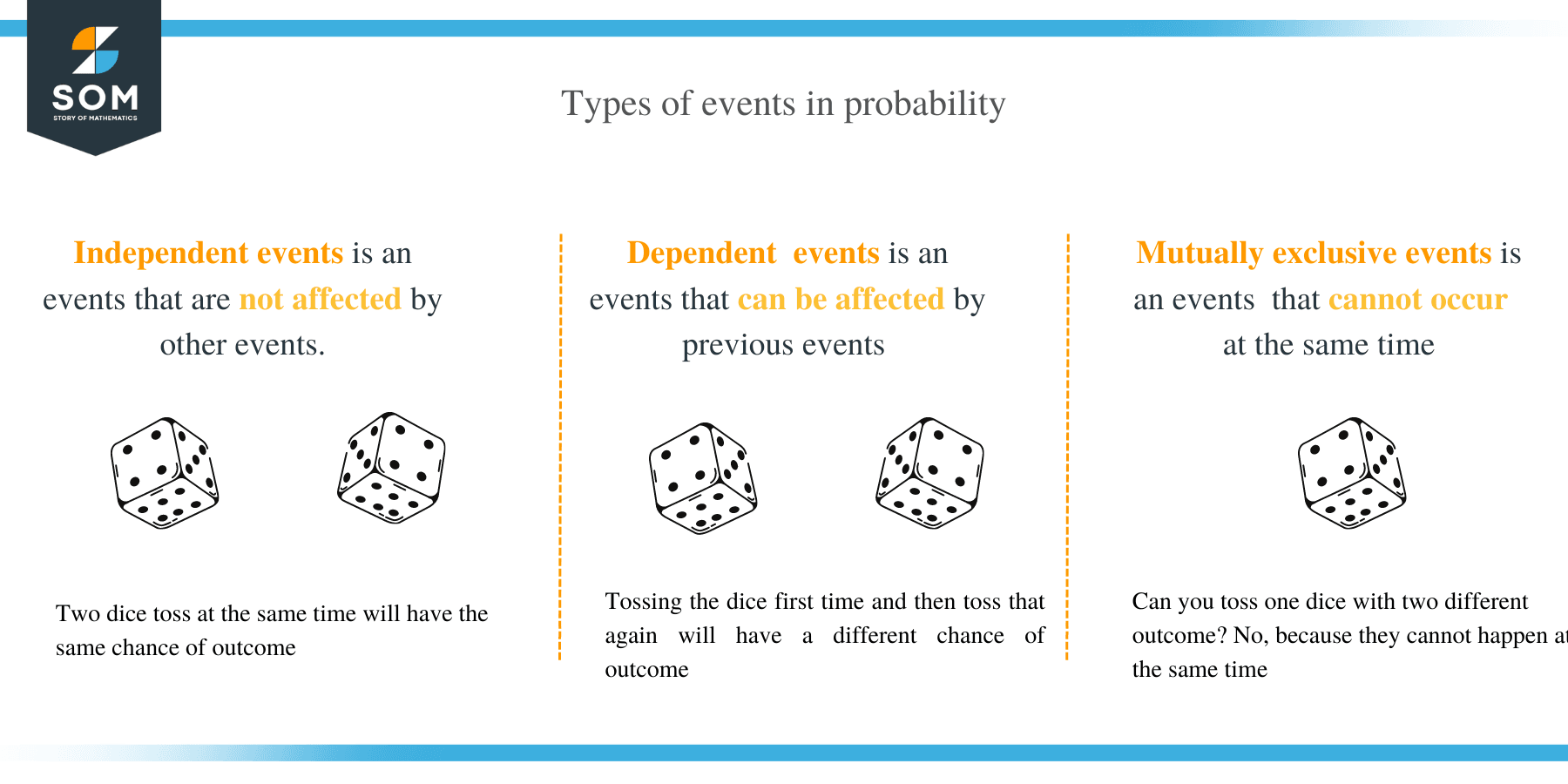
Events can either be independent, dependent, or mutually exclusive. Let’s define these types of events.
Types of Events
Independent Events
Events that are not affected by other events are known as independent events.
For example, you may roll a die and get a 1. You had a $\frac{1}{6}$ chance of getting that 1. Should you roll the die again, you still have a $\frac{1}{6}$ chance of getting a 1. You also have a $\frac{1}{6}$ chance of getting any other number on the die. Getting a 1 on your first throw cannot prevent you from getting a 1 on your second throw. Neither can it predict that you will get another 1 on your second throw.
Similarly, if you roll a die and pick a card from a deck of cards, the chances of picking a jack cannot be affected by the chances of rolling a 1.
Dependent Events
Events that can be affected by a previous event are known as dependent events.
Let’s think about what would happen if we had a bag of 2 blue, 1 red, 3 white, 2 green, and 4 yellow marbles. You pick one marble from the bag and set it aside. If you wanted to know the chances of picking a blue marble on the second try, that chance would affected by the first event. This is because the bag now has less marbles in total. The bag could possibly also have less blue marbles since the first marble could have been blue.
When the chances of the an event depend on the result of another, they are considered to be dependent events.
Mutually Exclusive Events
Events that cannot occur at the same time are called mutually exclusive events.
Do you think you could roll a 1 and a 2 at the same time with the same die? What about getting an Ace that is a Jack from a deck of cards? Well, you certainly cannot. That is because these events are mutually exclusive; they cannot happen at the same time.
How do you find the probability of an event?
For each of the types of events we have discussed, there will be different strategies for finding the probability of an event. You can learn more about that in the articles on the specific topic. However, in this section we will go through the general method for finding the probability of an event
The probability of an event is found by taking the number of outcomes favorable to the event and dividing it by the total possible outcomes of the experiment.
This is expressed mathematically as:
$P(E) = \frac{\text{number of outcomes favorable to the event}}{\text{total possible outcomes of the experiment}}$
Where E is used to denote the event.
Let’s examine a few examples.
Example 1: Find the probability of getting a blue marble from a bag with 1 blue marble, 1 green marble, and 1 orange marble.
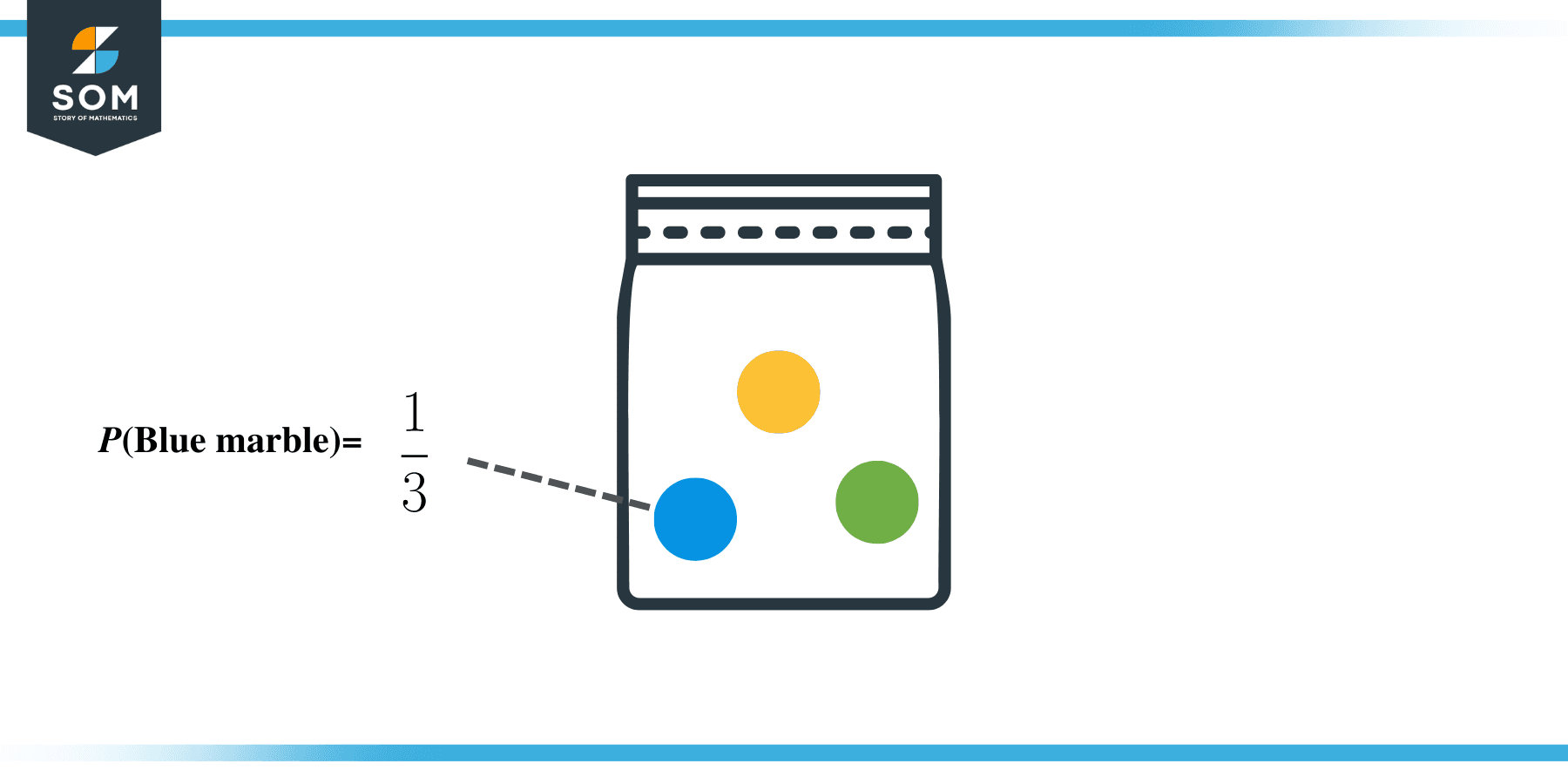
- The number of blue marbles in the bag is 1. So the number of outcomes favorable to the event is 1.
- The total possible number of outcomes of the experiment is 3 as there are three marbles in the bag.
- Thus, the probability of getting a blue marble is:
$P(\text{blue marble}) = \frac{1}{3}$
Example 2: The probability of pulling a 3 from a 52-card deck of playing cards.
- There are 4 outcomes favorable to the event since there are four 3’s in the deck.
- There are 52 total cards in the deck.
- Thus, the probability of getting a 3 is:
$P(3) = \frac{4}{52} = \frac{1}{13}$
It is perfectly okay to simplify the fraction that you get. In fact, you may even write the probability as a decimal. Probabilities of events are written as decimals in most applications.
Example 3: What is the probability of getting a head when you toss a coin?
- There is 1 outcome favorable to the event of getting a head.
- There are two possible outcomes of the experiment.
- Thus, the probability of getting a head is:
$P(\text{Head}) = \frac{1}{2} = 0.5$
Alternatively we can say there is a 50% chance of getting a head.
This is a good point to mention the possible values of a probability. In the above example we said there is a 50% chance of getting a head. If that is the case, then there must also be a 50% chance of getting a tail. Remember that a percent is of 100. This says something about the highest value we can get. Read on to learn more.
Possible Numerical Values of a Probability
Certain Events
Certain events are events that are sure to happen. There is a 100% chance that they will happen. Their probability is 1. That is:
$P(E) = 1$
Let’s think of a few certain events.
Example 1: The probability that a ball that has been thrown up will fall
Example 2: The probability of getting a whole number when you toss a die
Example 3: The probability of getting a head or a tail when you toss a coin.
Impossible Events
These are the opposite of certain events. As the name suggests, impossible events are those that can never occur. Thus:
$P(E) = 0$
This is the lowest extreme and 0 is the lowest value a probability can take. Events with a probability of 0 are impossible. Let’s think of a few.
Example 1: The probability of throwing a 6 sided die and getting a 7.
Example 2: The probability of buying a shirt from a store that only sells shoes.
Example 3: The probability of living forever
All Events
From the two cases above, we can conclude that the probability of all events fall between 0 and 1. That is:
$0 ≤ P(E) ≤ 1$
All of our examples have confirmed this and you may use this as a guide to self-check when computing your probabilities. If you get an answer outside of this range, the probability that your answer is incorrect, is 1.
Here’s a final example. Jake is trying to catch a bus that is numbered 54 at a bus stop that has the buses numbered 52, 54, 42, and 49 passing by. Each route number has 3 buses passing in any given hour. What is the probability that in a given hour Jake will catch his bus?
Solution:
- In a given hour, there are 3 buses running the route that Jake needs to catch, the 54
- In a given hour, there are 12 buses passing Jake’s stop, 3 of each of the 4 routes
- Thus:
$P(\text{Jake catches a 54 in any given hour}) = \frac{3}{12} = \frac{1}{4}$
Now it’s your turn to try some examples.
Examples
What is the probability of each of the following events?
- Getting an odd number when you toss a die?
- Choosing an apple from a bag with 2 apples, 2 bananas, and 1 pear.
- Throwing a 1 and a 2 when you toss 2 dice.
- Throwing a 1 or a 2 when you toss 2 dice.
- Pulling an Ace from a deck of cards on the second try if a King was removed on the first
Solutions
1.Getting an odd number when you toss a die?
$P(\text{odd number}) = \frac{3}{6} = \frac{1}{2}$
2. Choosing an apple from a bag with 2 apples, 2 bananas, and 1 pear.
$P(\text{apple}) = \frac{2}{5}$
3. Throwing a 1 and a 2 when you toss 2 dice.
- We can either get (1, 2) or (2, 1)
- There are 6 × 6 = 36 total outcomes
$P(\text{1 AND 2}) = \frac{2}{36} = \frac{1}{18}$
4. Throwing a 1 or a 2 when you toss 2 dice.
(Refer to article on sample space to see how many outcomes have a 1 and how many have a 2)
$P(\text{1 OR 2}) = \frac{24}{36} = \frac{2}{3}$
5. Pulling an Ace from a deck of cards on the second try if a King was removed on the first
- The first try was a King so we still have 4 Aces remaining
- The first try subtracts 1 from the total number of possible outcomes of the experiment
$P(\text{Ace on second try when king on first}) = \frac{4}{51}$
Some of these questions could have been solved using other methods. Check out the upcoming articles on types of events to learn more