- Home
- >
- Rational function holes – Explanation and Examples
Rational Function Holes – Explanation and Examples
 Ever noticed those hollowed dots or points that functions sometimes have? These are called the holes of rational functions. Curious as to why these points remain unfilled?
Ever noticed those hollowed dots or points that functions sometimes have? These are called the holes of rational functions. Curious as to why these points remain unfilled?
The holes in a rational function are the result of it sharing common factors shared by the numerator and denominator.
These are coordinates that the function passes through but are not part of the function’s domain and range.
When a function contains holes, we actually need them as guide points when graphing the function’s curve. But to highlight that they are not part of the function’s solutions, we leave them as unfilled dots.
Don’t worry. We’ll learn more about holes and how we can manipulate rational functions to find them in the next sections. We’ll also learn how to find the expressions of rational functions based on their holes, intercepts, and asymptotes.
What is a hole in a rational function?
When a rational function’s numerator and denominator share a common factor, $x- a$, a hole is found at $\boldsymbol{(a, f(a))}$. This also means that $a$ will not be included in the domain of the function.
What do these holes represent? These are the values or the coordinates that a function’s graph may pass through but are not defined by the function, hence, the unfilled dots.
Let’s take a look at the graph shown below to understand a rational function’s holes better.
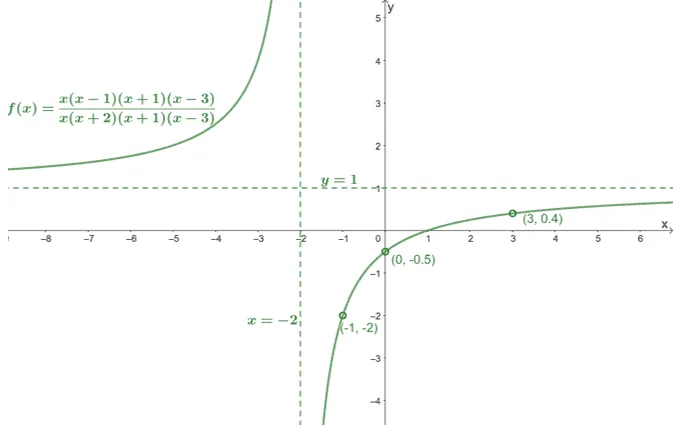
The graph shown above contains three unfilled points at: $(-1, -2)$, $\left(0, -\dfrac{1}{2}\right)$, and $\left(3, \dfrac{2}{5}\right)$. This means that the function has three holes as well.
The graph shows that the graph has discontinuities at the hole and its vertical asymptote at $x = -2$. Hence, our particular example has the following domain and range:
| Domain | $(-\infty, -2) \cup (-2, -1) \cup (-1, 0) \cup (0, 3) \cup (3, \infty)$ |
| Range | $(-\infty, -2) \cup (-2, -0.5) \cup (-0.5, 0.4) \cup (0.4, 1) \cup (1, \infty)$ |
How to find holes in a rational function?
Now that we understand the importance of understanding what the holes of rational functions represent, it’s time that we learn how to determine holes that a function may have.
Here are some helpful steps to remember when finding the holes of a rational function:
- Express the rational function’s numerator and denominator in factored form.
- Look out for common factors shared by the numerator and denominator.
- Equate each common factor to $0$, then solve for $x$.
- Simplify the function’s expression.
- Substitute the values of $x$ from Step 3 into the function’s simplified expression to find the hole’s $y$-coordinate.
- Write the hole as a coordinate, $(x, y)$, using the values from Step 3 and Step 5.
Yes, you might have guessed right. Finding holes in rational functions will require us to apply our knowledge on factoring, so check out these factoring techniques we’ve written in the past if you need a refresher:
- Learn about factoring trinomials here.
- Review your knowledge of factoring by grouping.
- Whenever possible, don’t forget to apply helpful properties such as the difference of two squares and the perfect square trinomial.
Why don’t we apply the six steps mentioned to find the holes of $f(x) = {-3x^3 + 6x^2 + 3x – 6}{4x^3 – 4x}$?
First, let’s express both the numerator and denominator of $f(x)$ in factored form.
Now that $f(x)$ is in factored form note the common factors shared between the numerator and denominator. For our case, we have $x – 1$ and $x + 1$.
This means that there are holes at $x= -1$ and $x = 1$. To find their corresponding $y$-coordinates, substitute these values for $x$ into the simplified form of $f(x)$.
$\begin{aligned}f(x) &= \dfrac{-3\cancel{(x – 1)}\cancel{(x + 1)}(x – 2)}{ 4x\cancel{(x – 1)}\cancel{(x + 1)}}\\&=-\dfrac{3(x-2)}{4x}\end{aligned}$
| $\boldsymbol{x}$ | $\boldsymbol{f(x)} =-\dfrac{3(x-2)}{4x}$ | $\boldsymbol{(x, y)}$ |
| $-1$ | $-\dfrac{9}{4}$ | $\left( -1, \dfrac{9}{4}\right)$ |
| $1$ | $\dfrac{3}{4}$ | $\left( 1, \dfrac{3}{4}\right)$ |
This means that $f(x)$ has holes at $\left( -1, \dfrac{9}{4}\right)$ and $\left( 1, \dfrac{3}{4}\right)$.
These will be presented as unfilled points that the graph of $f(x)$ will pass through.
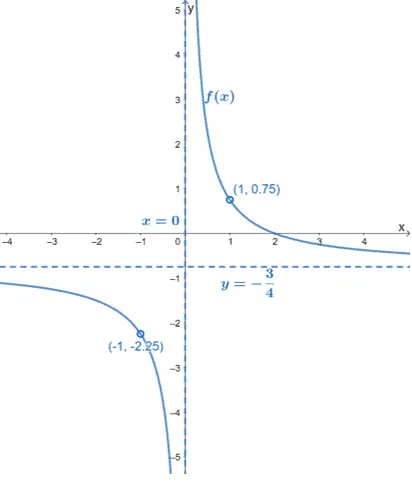
Here’s the graph of $f(x)$ along its holes and asymptotes. This confirms that the function’s curve can pass through these holes, but these values will not be part of the function’s domain and range.
Why don’t we write down $f(x)$’s range and domain?
| Domain | $(\infty, -1) \cup (-1, 0) \cup (0, 1) \cup (1, \infty)$ or $ x\in \mathbb{R}: \{x \neq -1, x \neq 0, x \neq 1\}$ |
| Range | $\left(\infty, -\dfrac{9}{4}\right) \cup \left(-\dfrac{9}{4}, -\dfrac{3}{4}\right) \cup \left(-\dfrac{3}{4}, \dfrac{3}{4}\right) \cup \left(\dfrac{3}{4}, \infty\right)$ or $y\in \mathbb{R}: \left \{y \neq – \dfrac{9}{4}, y \neq – \dfrac{3}{4}, y \neq \dfrac{3}{4} \right\}$ |
Ready to try out more problems? Don’t worry, we’ve prepared some for you! Make sure to review all the techniques and steps mentioned in this article.
Example 1
Find the holes found in the following rational functions.
a. $f(x) = \dfrac{-2(x – 1)(x + 2)(x + 3)}{x^2(x – 1)(x + 4)(x – 3)}$
b. $g(x) = \dfrac{x^2 – 25}{x^2 – 9x + 20}$
c. $h(x) = \dfrac{x^3 – 7x + 6}{x^4 + 4x^3 +x^2 – 6x}$
Solution
Since $f(x)$’s numerator and denominator are already in factored form, we can check them for common factors. For this function, we can see that $(x -1)$ is a factor shared by the numerator and denominator, so there is a hole at $x = 1$.
Simplify $f(x)$ then substitute $x = 1$ into the simplified form of $f(x)$.
$ \begin{aligned} f(x) &= \dfrac{-2\cancel{(x – 1)}(x + 2)(x + 3)}{x^2\cancel{(x – 1)}(x + 4)(x – 3)}\\ &=\dfrac{-2(x + 2)(x+3)}{(x+4)(x-3)}\\\\f(1)&= \dfrac{-2(1 +2)(1 +3)}{(1 + 4)(1 – 3)}\\&=\dfrac{-2(12)}{5(-2)}\\&=\dfrac{12}{5}\end{aligned}$
a. This means that $f(x)$ has a hole at $\left(1, \dfrac{12}{5}\right)$.
Factor the numerator and the denominator of $g(x)$ first then rewrite $g(x)$.
$\begin{aligned} g(x)&=\dfrac{x^2 – 25}{x^2 – 9x + 20} \\&= \dfrac{(x – 5)(x +5)}{(x-4)(x-5)}\end{aligned}$
We can see that $x – 5$ is a common factor shared by the numerator and denominator, so simplify $g(x)$ then substitute $x = 5$ into the simplified form of $g(x)$.
$\begin{aligned} g(x)&=\dfrac{\cancel{(x – 5)}(x +5)}{(x-4)\cancel{(x-5)}}\\&=\dfrac{x+5}{x-4}\\\\g(5)&= \dfrac{5 + 5}{5 – 4}\\&=10\end{aligned}$
b. From this, we can see that $g(x)$ has a hole at $(5, 10)$.The numerator and denominator of $h(x)$ have higher degrees than the previous examples, so let’s break down the factoring process done on both.
| Numerator | $ \begin{aligned} x^3 – 7x + 6 &= x^3 – x – 6x + 6\\&=x(x^2-1) -6(x -1)\\&=x(x-1)(x + 1) -6(x -1)\\&=(x-1)[x(x+1)-6]\\&=(x-1)(x^2 + x -6)\\&=(x -1)(x – 2)(x +3)\end{aligned}$ |
| Denominator | $ \begin{aligned} x^4 + 4x^3 +x^2 – 6x &= x(x^3 + 4x^2 +x – 6)\\&=x(x^3 +3x^2 +x^2+x-6)\\&=x[x^2(x+3)+ (x-2)(x +3)]\\&=x[(x+3)(x^2 + x -2)]\\&=x[(x+3)(x -1)(x +2)]\end{aligned}$ |
| $h(x) = \dfrac{( x -1)(x – 2)(x +3)}{ x(x+3)(x -1)(x+2)}$ | |
We can see that $h(x)$’s numerator and denominator share common factors of $x – 1$ and $x + 3$. Simplify $h(x)$ and substitute each of these values into the simplified form of $h(x)$.
$ \begin{aligned} h(x) &= \dfrac{\cancel{( x -1)}(x – 2)\cancel{( x + 3)}}{ x\cancel{( x + 3)}\cancel{( x -1)}(x+2)}\\&= \dfrac{x – 2}{x(x + 2)}\end{aligned}$
| $\boldsymbol{x}$ | $\boldsymbol{h(x)} =\dfrac{x-2}{x( x + 2)}$ | $\boldsymbol{(x, y)}$ |
| $-3$ | $-3 $ | $(-3, -15)$ |
| $1$ | $1$ | $(1, -3)$ |
c. This means that $h(x)$ has holes at $(-3, -15)$ and $(1, -3)$.
Example 2
The graph of $f(x)$ passes through the $x$-intercepts, $(-2, 0)$ and $(-1, 0)$, and its graph is also shown below.
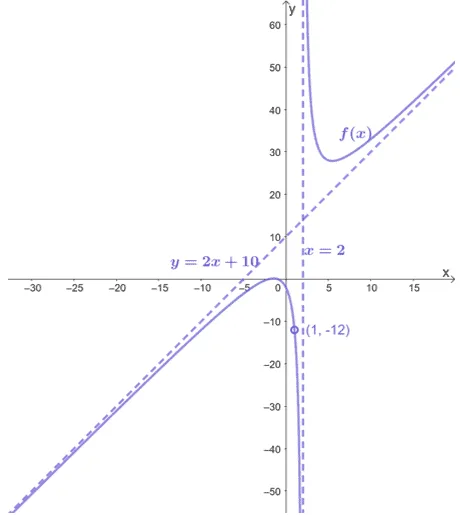
Use the information provided to find an expression that may represent $f(x)$.
Solution
Since we have $(-2, 0)$ and $(-1, 0)$ as the function’s $x$-intercept, the numerator of $f(x)$ has $(x + 2)$ and $(x + 1)$ as factors.
The graph shows a hole at $x = 1$, so $x – 1$ is a common factor shared by the numerator and the denominator.
Why don’t we write down what we have so far?
$f(x) = a\dfrac{(x + 2)(x + 1)(x – 1)}{(x – 1)}$
The variable $a$ represents the constant that we may need for $f(x)$.
Considering that there is a vertical asymptote at $x = 2$, the denominator has $x -2$ as a factor.
$f(x) = a\dfrac{(x + 2)(x + 1)(x – 1)}{(x – 1)(x – 2)}$
When $f(x)$ is simplified and we substitute $x = 1$, we can equate the result to $-12$ to find $a$.
$ \begin{aligned} f(1)&=a\dfrac{(1 + 2)(1 + 1)}{1 – 2}\\&=a \cdot \dfrac{6}{-1}\\&=-6a\\\\-12&=-6a\\a&=2\end{aligned}$
This means that the graph can be represented by $f(x) = \dfrac{2(x + 2)(x + 1)(x – 1)}{(x – 1)}$.
Check out these additional problems to test your knowledge of rational functions and their holes.
Practice Questions
![]()
Images/mathematical drawings are created with GeoGebra.
