Set Equality — Definition & Examples

Sets are one of the most fundamental concepts in mathematics. We have already discussed the basic classification of sets in previous lessons. Now let’s take a look at one of the most important set operations — Set Equality.

This article will explain the concept of Set Equality to help you understand them better.

Two sets are said to be equal if they contain the same elements and the same cardinality. This concept is known as Set Equality.

We will cover the following topics in this article:

• What is set equality?
• How to show that two sets are equal?
• Properties of equal sets.
• Examples
• Practice problems

What is Set Equality?

When young math enthusiasts dive into sets for the first time, they often ask, “what is set equality?” So let’s address this question.

Set equality is the term that is used to indicate that two sets are equal. Any two sets, finite or infinite, are equal if they contain the same elements.

Consider two sets, A and B. These two sets are only equal if and only if each element of set A also exists in set B. The order of the two sets’ elements does not matter as long as the elements are the same. Let’s consider the following two sets, A and B, to understand this statement.

A = {1, 2, 3, 4}

B = {2, 4, 1, 3}

By observing the two sets A and B, it is evident that although the two sets A and B are different, they contain the same elements.

Another factor to consider while analyzing the set equality is that the two equal sets also have the same set size, i.e., equal cardinality. Hence, as long as the two sets have the same elements and equal cardinality, they will be classified as equal sets.

Let’s solve an example to comprehend this concept.

Example 1

Determine which of the following sets are equal sets:

(i) A = {55, 32, 77, 1} and B = {1, 32, 55, 77}

(ii) X = {x : x is a prime number and 2<x<11} and Y = {7, 3, 5}

(iii) S = {2, 4, 6, 8} and T = {2, 4, 6}

Solution

(i) To determine the set equality, we have to consider two things; set elements and set cardinality. The cardinality of set A and B:

|A| = 4

And,

|B| = 4

So,

|A| = |B|

Both sets A and B have the same elements, which are 1, 32, 55, and 7.

Hence, sets A and B are equal sets.

(ii) To determine set equality, let’s first simplify set X.

X = {x : x is a prime number and 2<x<11}

So,

X = {3, 5, 7}

Now, let’s find the cardinality.

|X| = 3

And,

|Y| = 3

So,

|X| = |Y|

Also, both sets have the same elements, which are 3, 5, and 7.

Hence, sets X and Y are equal sets.

(iii) To determine set equality, let’s calculate the cardinality first.

|S| = 4

And,

|T| = 3

As

|S| ≠ |T|

So the two sets, S and T, are not equal sets.

Representation of Equal Sets through Venn Diagram

In previous lessons, we have discussed the importance of Venn diagrams and how we can use them to depict different operations. Equal sets can also be represented through the Venn diagram, and their relation can be portrayed through the intersection operation. 

For this purpose, consider two sets, A and B. Let set A = {2, 6, 8} and set B = {6, 8, 2}. Their representation through the Venn diagram is as follows:

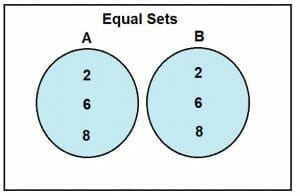
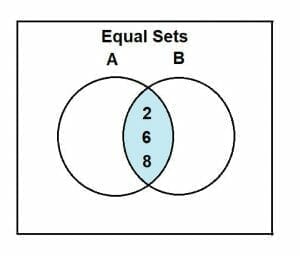
As these sets are equal, so their intersection would be as follows:

A ∩ B = {2, 6, 8}

Hence, 

A ∩ B = A = B

Which shows that A and B are equal sets. 

How to Show that Two Sets are Equal?

Suppose you have a collection of data involving multiple sets. We have already covered how you are going to classify these sets. But what if some sets are identical? How will you identify these identical or equal sets? To answer these questions, we need to understand how to identify that two sets are equal.

To show that two sets are equal, both the sets need to be subsets of one another. A subset is a baby set that contains all or some of the elements of the parent set. The symbol ⊆ is used to indicate a subset.

Earlier, we mentioned that they need to be a subset of one another for two sets to be equal.

Mathematically we can express it as follows:

If A ⊆ B

And B ⊆ A

Then,

A = B

If this condition of subsets is not satisfied, then the two sets are not equal sets.

Let’s solve the following examples to understand this identification.

Example 2

Let set A = {3, 6, 9, 12} and set B = {9, 12, 6, 3}. Evaluate whether the two sets are equal or not.

Solution

To evaluate whether the sets are equal, we will apply the above concept of subsets.

The elements of A are 3, 6, 9, and 12.

The elements of B are 9, 12, 6, and 3.

It is clear that,

A ⊆ B

And also,

B ⊆ A

Hence,

A = B

Therefore, the two sets A and B are equal.

Example 3

Let X = {x : x is even number and 4<x<10} and Y = {y: y is multiple of 2 and 4<y<10}. Determine if the two sets are equal sets.

Solution

To determine the set equality, we will first simplify these sets.

Set A can be rewritten as:

A = {6, 8}

Set B can be rewritten as:

B = {6, 8}

Now, we will apply the concept of subsets.

The elements of A are 6 and 8.

The elements of B are also 6 and 8.

It is clear that,

A ⊆ B

And also,

B ⊆ A

Hence,A = B

Therefore, the two sets A and B are equal.

We will now solve some examples merging the concept of subsets and cardinality to determine the set equality.

Example 4

If set A = {1, 3, 5, 7, 9} and set B = {x : x is an odd number and 1≤x<11}, then determine if the two sets are equal.

Solution

To determine the set equality, we will first simplify the sets.

Set B can be rewritten as:

B = {1, 3, 5, 7, 9}

Now, let’s evaluate their cardinality.

|A| = 5

And,

|B| = 5

So,

|A| = |B|

This proves that the two sets are equal.

Now let’s evaluate the set equality through subsets.

The elements of set A are 1, 3, 5, 7, and 9.

The elements of set B are 1, 3, 5, 7, and 9.

As

A ⊆ B

And also,

B ⊆ A

Hence,

A = B

Therefore, the two sets A and B are equal.

To further strengthen the understanding and the concept of the set equality, consider the following practice problems.

Practice Problem

1. Determine if the following sets are equal:

        (i) A = {10, 20, 30} and B = {20, 10}

        (ii) X = {122, 133, 144} and B = {144, 122, 133}

2. If A = {x : x is an odd number and 3<x<10} and B = {x : x is an even number and 3<x<10}, find if the two sets are equal by evulatihng cardinality.

3. If X = {30, 45, 78, 12} and B = {45, 12, 78, 30}, then find if the sets are equal by evaluating subsets.

Answers

1. (i) Not equal (ii) Equal
2. Not Equal
3. Equal

Previous Lesson | Main Page | Next Lesson