JUMP TO TOPIC
Empty Set – Definition & Examples
In our previous lessons, we have covered the classification of countable and uncountable items. But there are plenty of possibilities and open doors in the world of mathematics. So, what happens when the items for classification are neither countable nor uncountable?
We know this question may sound confusing, but questions like this give birth to a new concept in the realm of set classification. The answer to this question is Empty Sets.
This article will explain what Empty Sets are so you can understand them better and know when, where, and how to use them.
Empty sets are the sets that contain no elements. Since these sets are empty, they are also called void sets.
We will cover the following topics in this article:
- What is an empty set?
- How to represent the empty set?
- Properties of empty sets.
- Examples
- Practice Problems
We also suggest you take a look at the following topics below for a quick refresher before we start diving into Empty Sets:
What is an Empty Set?
If you are a big mathematics fan, you may have asked the question, “what is an empty set?” especially when you have encountered specific problems that cannot be classified as either countable or uncountable. A standard classification that helps us deal with such problems is by classifying them into empty sets.
An empty set, as the name suggests, is empty and does not contain any elements.
These sets are made to simplify calculations and often used to classify the odd items or items that are rare. Some examples in which an empty set is used for classification include a month with 32 days, a week with 2 Mondays, a dog with five legs, or a solar system with no planets. In mathematical terms, an empty set may classify a whole number between 7 and 8. All these examples have no definite answers and hence are classified using an empty set.
Empty sets are unique sets and also possess a unique cardinality. We defined cardinality as the set size or the total number of elements in the set in our previous lessons. Since empty sets contain no elements, hence their cardinality is also zero.
Let’s solve an example to develop a firm understanding of empty sets.
Example 1
Determine which of the following is an empty set:
(i) X = {x : x is a natural number and 4<x<5}
(ii) Y = {y : y is a prime number and 8<y<10}
(iii) Number of cars with 10 doors.
Solution
(i) Consider the set of natural numbers N given below:
N = {1, 2, 3, 4, 5, 6, …}
As no natural number exists between 4 and 5, so the set X is an empty set.
(ii) Consider the set of prime numbers P
P = {2, 3, 5, 7, 11, …}
As no prime number exists between 8 and 10, so the set Y is an empty set.
(iii). In real life, and unless some car manufacturer creates a prototype, it’s impossible to find a car that has ten doors. So, the set containing the cars with ten doors is empty.
How to Represent an Empty Set?
Now that we know what an empty set is, the next topic addresses its representation.
Empty sets are represented by the conventional curly brackets { } which are used to notify sets. However, since these sets are unique, they can also be represented by the special character $\phi$ .
Empty sets contain no elements in them, and they are represented by empty curly brackets { }. Consider an empty set A that has no elements. The notation of this set is:
A = { }
In the previous lessons, we mentioned that we could also represent infinite sets by any letter, word, or phrase. Thus, the same empty set A can have the following notations as well:
Empty set = { }
Or
X = { }
We can also use the symbol $\phi$ to represent an empty set. An example is shown below:
$\phi$ = {x : x is a multiple of 5 and 2<x<4}
Since no multiples of 5 exist between 2 and 4, so the set is an empty set.
Some examples of empty sets are as follows:
Example 2
Determine if the following sets are empty:
(i) A = {x : x is the common point of two parallel lines}
(ii) B = {x : x is an even natural number divisible by 3}
Solution
(i) The definition of parallel lines states that these two lines never intersect and thus, they do not have a common point. So, the given set is an empty set and can be written as:
A = { }
Or
$\phi$ = {x : x is the common point of two parallel lines}
(ii) The given set is an empty set since there is no even natural number that is divisible by 3. We can re-write it as follows:
B = { }
Or
$\phi$ = {x : x is an even natural number divisible by 3}
The difference between a Zero Set and an Empty Set
Many people often mistake the concept of zero sets and calling them empty sets. They claim that the two are of similar classifications. This is not true. We can understand this better by analyzing the definitions of these two sets.
An empty set is a set containing no elements, whereas, the zero set is a set that contains zero. Upon inspecting the definitions, it is evident that an empty set contains no elements at all, whereas, the zero contains one element which is zero.
This difference between the two sets makes the empty set even more unique due to its element-less feature. Therefore, the two sets are distinct as one set contains no element while the other set, the zero set, contains one element.
The following example will help us understand this difference better.
Example 3
Consider a set A = {0} and a set B = {x : x is an odd number divisible by 2}. Differentiate between the two sets.
Solution
To differentiate between these two sets, let’s first simplify them:
A = {0}
It is clear from set B that there is no odd number that is divisible by 2; hence, set B is an empty set. Set B can be written as follows:
B = { }
Or
$\phi$ = B
It is evident that set B is an empty set, whereas set A is a zero set. This is the major difference between the two sets A and B.
Representation of Empty Set through Venn Diagram
Venn Diagrams are the most effective medium to represent sets, especially finite sets. These diagrams are also used to depict the relations of union and intersection between two sets.
An empty set can be represented through a Venn diagram and the relation of the intersection. The relation and presentation are as follows: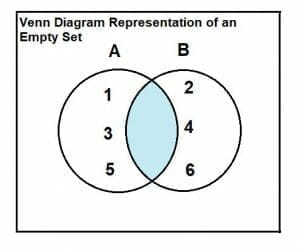
Consider a set A = {1, 3, 5} and a set B = {2, 4, 6}.
As it is clear from the Venn diagram that there are no common or intersecting elements between the two sets, hence the intersection between the two sets is empty.
A∩B = $\phi$
Let’s consider an example relating to this concept.
Example 4
Let set A = {3, 6, 9} and set B = {4, 8, 10}. Find the intersection between the 2 sets.
Solution
We can solve this example with the help of a Venn diagram.
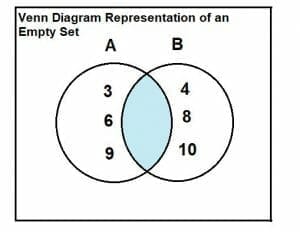
The two sets are indicated below. It is evident from the Venn diagram that there are no common or intersecting elements between the two sets. Hence, the intersection of the two sets is an empty set.
A∩B = $\phi$
Properties of an Empty Set
Empty sets play a phenomenal role in the classification of unique and odd objects. Not only do these empty sets provide ease in the classification aspect, but also help us to simplify the calculations. These empty sets are important through some of its properties that form the foundation of relevant calculations. So, to better grasp the concept of empty sets, let’s analyze these properties.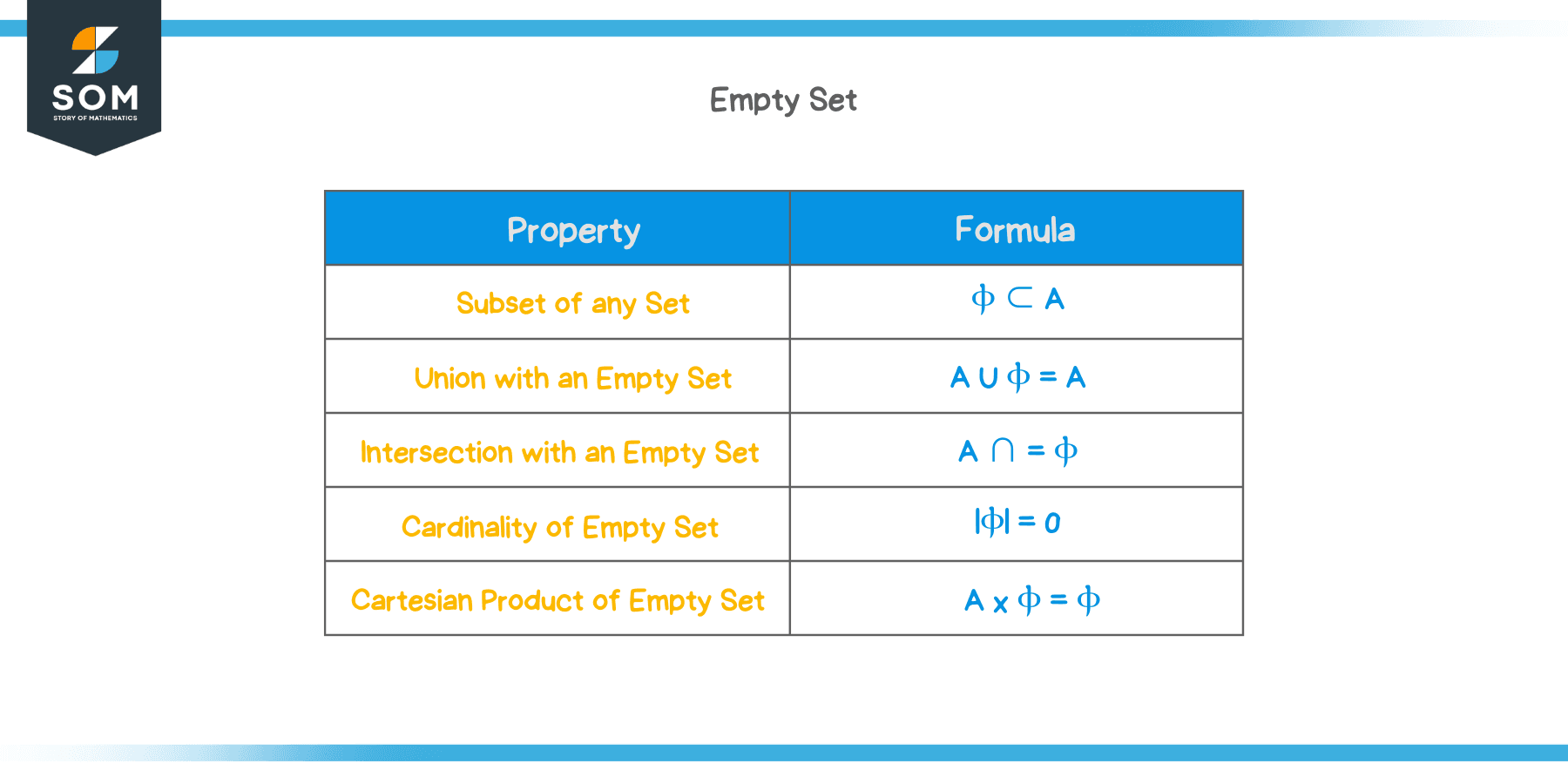 
1. Subset of any Set:
The empty set is the subset of any set A.
We can understand this property by considering any finite or infinite set A. If we chalk out all the possible subsets of set A, then we will always include an empty set in it as well.
For example, consider a finite set A = {1, 3, 5}
All the possible subsets of this set A are:
A = $\phi$ , A = {1}, A = {3}, A = {5}, A = {1,3}, A = {3, 5}, A = {1,5}
We have included an empty set amongst the list of subsets because of the following property:
$\phi$ ⊂ A
The same principle can be applied on infinite sets as well.
For infinite sets, consider an infinte set B = {1, 4, 6, …}.
The list of all the possible subsets of this set are the following:
B = $\phi$, B = {1, 4, ….}, B = {4, 6, …} etc.
And,
$\phi$ ⊂ B
Note that it does not matter whether a set is finite or infinite; an empty set will always be the subset of the given set.
Let’s see an example to understand this property.
Example 5
Consider a set X = {2, 4, 6}. List all its possible subsets.
Solution
To solve this example, we will consider the above property.
The list of all the subsets of set X is:
$\phi$, {2}, {4}, {6}, {2, 4}, {4, 6}, {2, 6}
An empty set is also a subset because of the following relation:
$\phi$ ⊂ X
2. Union with an Empty Set:
The union of any set with an empty set will always be the set itself.
Consider a finite set A. According to this property, the union of this set A with an empty set is as follows:
A U $\phi$ = A
Since an empty set contains no elements at all, its union with any set A produces the same set A as the results.
This set A can be both infinite or finite. The result is the same in both cases as the empty set contains no elements.
Let’s solve an example to verify this property.
Example 6
Consider a set A = {1, 2, 3, 4, 5, 6}. Find the union of this set A with an empty set.
Solution
An empty set contains no elements. The union of set A with the empty set is shown below:
A U $\phi$ = {1, 2, 3, 4, 5, 6} U { }
A U $\phi$ = {1, 2, 3, 4, 5, 6}
This proves the property that the union of any set with an empty set is the set itself.
3. Intersection with an Empty Set:
The intersection of any set with the empty set will always be an empty set.
Consider a set A. According to this property, the intersection is as follows:
A ∩ = $\phi$
Since the empty set contains no elements at all, there will be no common element between an empty and a non-empty set.
This set A can be both finite and infinite. The result is the same in both cases as the empty set contains no elements.
Let’s solve an example to verify this property.
Example 7
Consider a set A = {2, 4, 6, 8}. Find its intersection with the empty set.
Solution
An empty set contains no elements in it. The intersection of an empty set with the set A is like the following:
A ∩ $\phi$ = {2, 4, 6, 8}
A ∩ =$\phi$
Since the empty set has no elements, no common element exists between set A and the empty set.
4. Cardinality of Empty Set:
The cardinality of the empty set is always zero.
The cardinality is defined as the set size or the total number of elements in the set. Since empty sets contain no elements, hence they have a zero cardinality. This is shown below:
|$\phi$| = 0
Therefore, according to the above relation, the cardinality of the empty set will always be zero.
Let’s consider an example based on this property.
Example 8
Find set X’s cardinality where set X = {x: x is an odd multiple of 10}.
Solution
For solving this example, we will first simplify the set.
As there are no odd multiples of 10 in existence, hence the set is empty.
The cardinality can be found as:
|$\phi$| = |x : x is an odd multiple of 10|
|$\phi$ | = 0
5. Cartesian Product of Empty Set:
The Cartesian Product of an empty set will always be an empty set.
The Cartesian Product is the multiplication between two sets A and B, which produces ordered pairs. The Cartesian Product of any set with the empty set will always be empty because the empty set contains no elements.
So we can conclude:
A x $\phi$ = $\phi$
Let’s consider an example based on this property.
Example 9
Find the Cartesian Product of set A = {1, 2, 3, 4} with an empty set.
Solution
The Cartesian Product is the multiplication between the two sets. It is conducted as follows:
A x $\phi$ = {1, 2, 3, 4} x { }
A x $\phi$ = $\phi$
The result is the empty set because an empty set contains no elements, and its multiplication does not produce a definite result. This also verifies the property.
To further strengthen the understanding and the concept of the infinite set, consider the following practice problems.
Practice Problems
- Determine which of the following are empty sets:
(i) P = {set of prime numbers divisible by 10}
(ii) Q = {x : x is even prime number}
- Differentiate between the sets X and Y where X = {0} and Y = { }.
- List all the possible subsets of A = {3, 6, 9, …}.
- Find the union and intersection of A = {10, 20, 30, 50} with an empty set.
- Find the cardinality of B = {number of intersecting parallel lines in a plane}
Answers
- (i) Empty set (ii) Non-empty set
- Zero set, Empty set.
- { }, {3,…}, and so on.
- A, Empty set.
- zero