Solving Logarithmic Equations – Explanation & Examples

As you well know that, a logarithm is a mathematical operation that is the inverse of exponentiation. The logarithm of a number is abbreviated as “log.”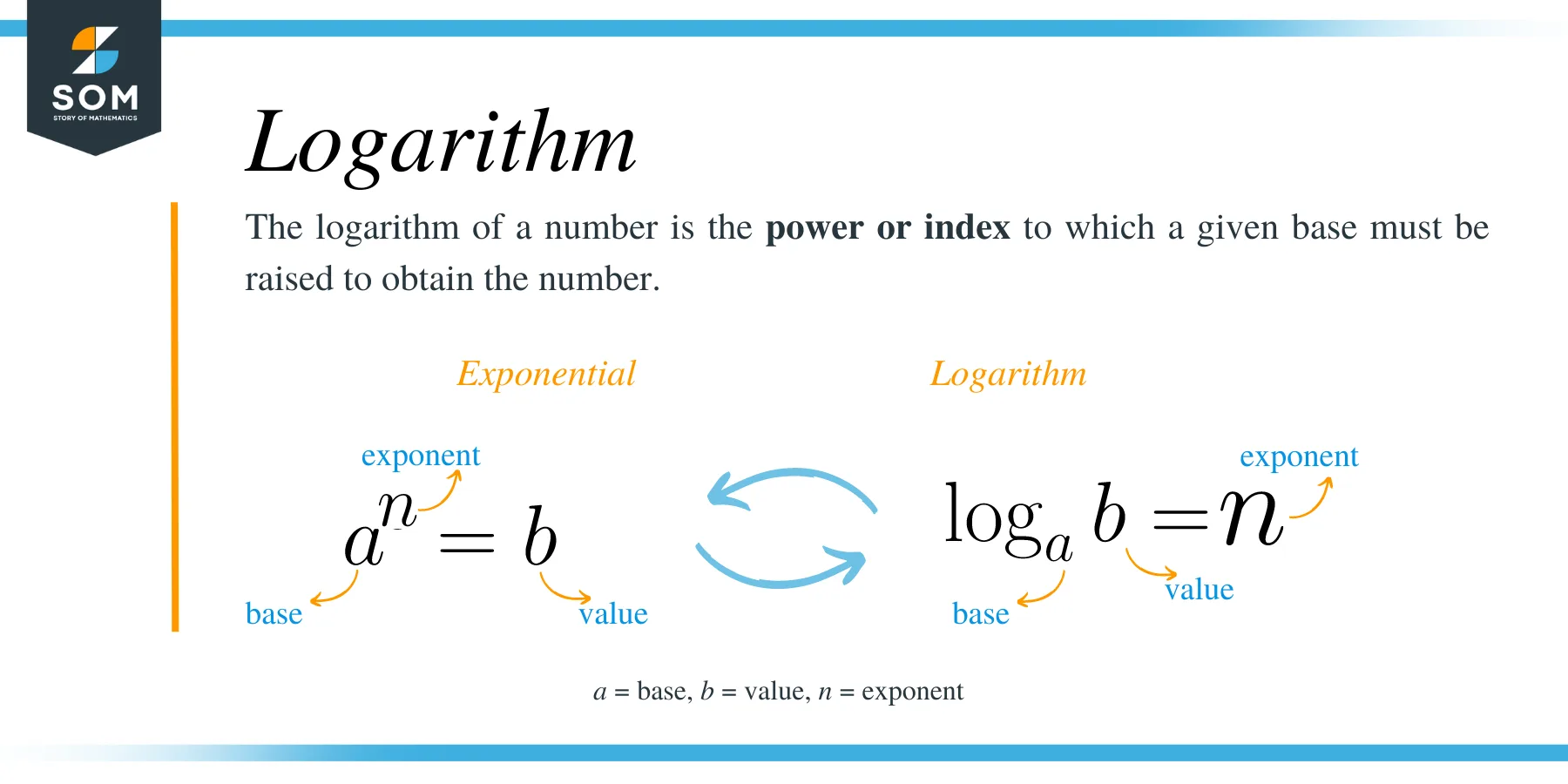

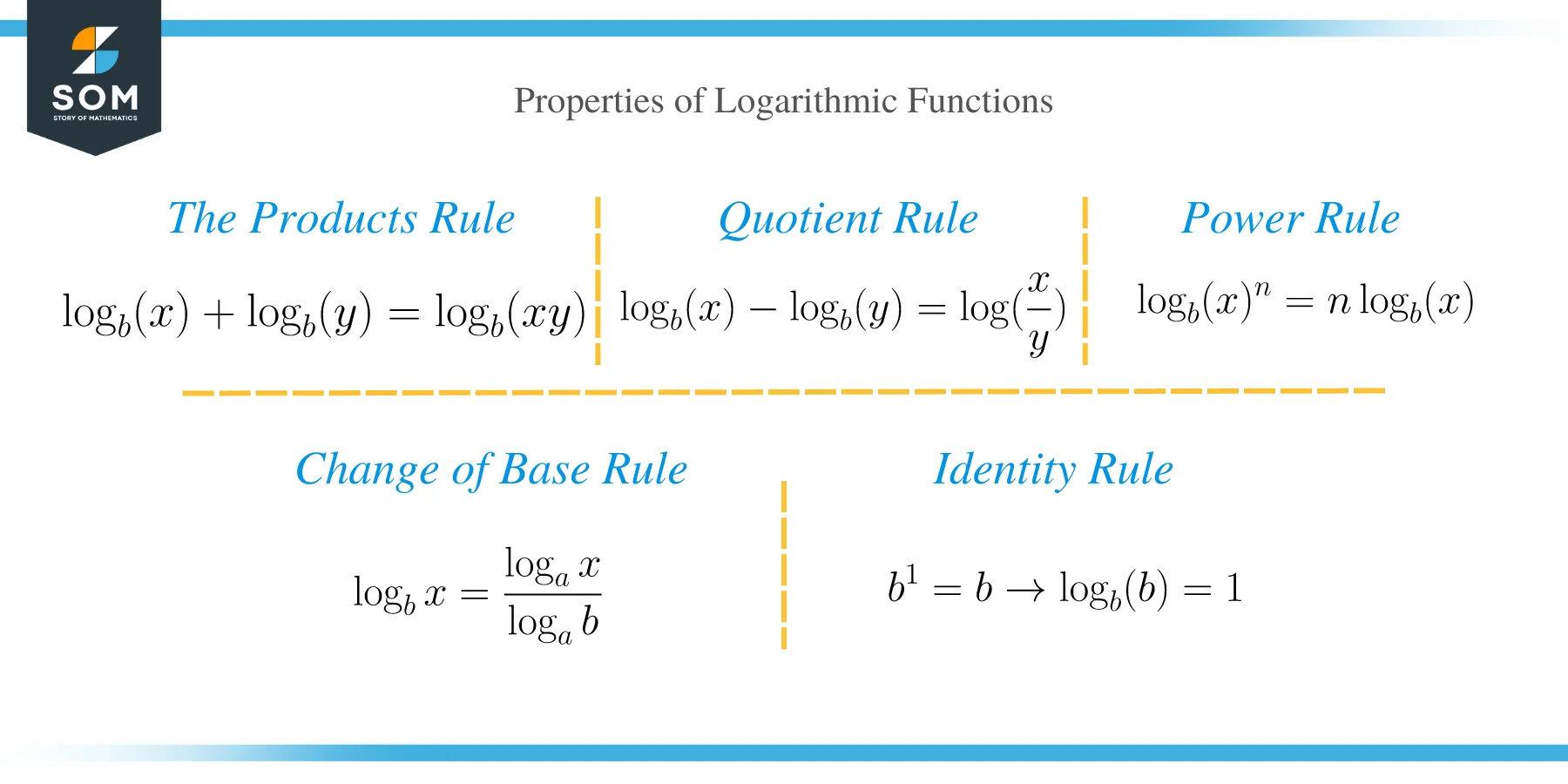
Before we can get into solving logarithmic equations, let’s first familiarize ourselves with the following rules of logarithms:

• The product rule:

The product rule states that the sum of two logarithms is equal to the product of the logarithms.  The first law is represented as;

⟹ log _b (x) + log _b (y) = log _b (xy)

• The quotient rule:

The difference of two logarithms x and y is equal to the ratio of the logarithms.

⟹ log _b (x) – log _b (y) = log (x/y)

• The power rule:

⟹ log _b (x) ⁿ = n log _b (x)

• Change of base rule.

⟹ log _b x = (log _a x) / (log _a b)

• Identity rule

The logarithm of any positive number to the same base of that number is always 1.
b¹=b ⟹ log _b (b)=1.

Example:

• The logarithm of the number 1 to any non-zero base is always zero.
  b⁰=1 ⟹ log _b 1 = 0.

How to Solve Logarithmic Equations?

An equation containing variables in the exponents is knowns as an exponential equation. In contrast, an equation that involves the logarithm of an expression containing a variable is referred to as a logarithmic equation.

The purpose of solving a logarithmic equation is to find the value of the unknown variable.

In this article, we will learn how to solve the general two types of logarithmic equations, namely:

1. Equations containing logarithms on one side of the equation.
2. Equations with logarithms on opposite sides of the equal to sign.

How to solve equations with logarithms on one side?

Equations with logarithms on one side take log _b M = n ⇒ M = b ⁿ.

To solve this type of equations, here are the steps:

• Simplify the logarithmic equations by applying the appropriate laws of logarithms.
• Rewrite the logarithmic equation in exponential form.
• Now simplify the exponent and solve for the variable.
• Verify your answer by substituting it back in the logarithmic equation. You should note that the acceptable answer of a logarithmic equation only produces a positive argument.

Example 1

Solve log ₂ (5x + 7) = 5

Solution

Rewrite the equation to exponential form

logs ₂ (5x + 7) = 5 ⇒ 2 ⁵ = 5x + 7

⇒ 32 = 5x + 7

⇒ 5x = 32 – 7

5x = 25

Divide both sides by 5 to get

x = 5

Example 2

Solve for x in log (5x -11) = 2

Solution

Since the base of this equation is not given, we therefore assume the base of 10.

Now change the write the logarithm in exponential form.

⇒ 10² = 5x – 11

⇒ 100 = 5x -11

111= 5x

111/5 = x

Hence, x = 111/5 is the answer.

Example 3

Solve log ₁₀ (2x + 1) = 3

Solution

Rewrite the equation in exponential form

log₁₀ (2x + 1) = 3n⇒ 2x + 1 = 10³

⇒ 2x + 1 = 1000

2x = 999

On dividing both sides by 2, we get;

x = 499.5

Verify your answer by substituting it in the original logarithmic equation;

⇒ log₁₀ (2 x 499.5 + 1) = log₁₀ (1000) = 3 since 10³ = 1000

Example 4

Evaluate ln (4x -1) = 3

Solution

Rewrite the equation in exponential form as;

ln (4x -1) = 3 ⇒ 4x – 3 =e³

But as you know, e = 2.718281828

4x – 3 = (2.718281828)³ = 20.085537

x = 5.271384

Example 5

Solve the logarithmic equation log ₂ (x +1) – log ₂ (x – 4) = 3

Solution

First simplify the logarithms by applying the quotient rule as shown below.

log ₂ (x +1) – log ₂ (x – 4) = 3 ⇒ log ₂ [(x + 1)/ (x – 4)] = 3

Now, rewrite the equation in exponential form

⇒2 ³ = [(x + 1)/ (x – 4)]

⇒ 8 = [(x + 1)/ (x – 4)]

Cross multiply the equation

⇒ [(x + 1) = 8(x – 4)]

⇒ x + 1 = 8x -32

7x = 33 …… (Collecting the like terms)

x = 33/7

Example 6

Solve for x if log ₄ (x) + log ₄ (x -12) = 3

Solution

Simplify the logarithm by using the product rule as follows;

log ₄ (x) + log ₄ (x -12) = 3 ⇒ log ₄ [(x) (x – 12)] = 3

⇒ log ₄ (x² – 12x) = 3

Convert the equation in exponential form.

⇒ 4^{3 =} x² – 12x

⇒ 64 = x² – 12x

Since this is a quadratic equation, we therefore solve by factoring.

x² -12x – 64 ⇒ (x + 4) (x – 16) = 0

x = -4 or 16

When x = -4 is substituted in the original equation, we get a negative answer which is imaginary. Therefore, 16 is the only acceptable solution.

How to solve equations with logarithms on both sides of the equation?

The equations with logarithms on both sides of the equal to sign take log M = log N, which is the same as M = N.

The procedure of solving equations with logarithms on both sides of the equal sign.

• If the logarithms have are a common base, simplify the problem and then rewrite it without logarithms.
• Simplify by collecting like terms and solve for the variable in the equation.
• Check your answer by plugging it back in the original equation. Remember that, an acceptable answer will produce a positive argument.

Example 7

Solve log ₆ (2x – 4) + log _{6 (}4) = log ₆ (40)

Solution

First, simplify the logarithms.

log ₆ (2x – 4) + log ₆ (4) = log ₆ (40) ⇒ log ₆ [4(2x – 4)] = log ₆ (40)

Now drop the logarithms

⇒ [4(2x – 4)] = (40)

⇒ 8x – 16 = 40

⇒ 8x = 40 + 16

8x= 56

x = 7

Example 8

Solve the logarithmic equation: log ₇ (x – 2) + log ₇ (x + 3) = log ₇ 14

Solution

Simplify the equation by applying the product rule.

Log ₇ [(x – 2) (x + 3)] = log ₇ 14

Drop the logarithms.

⇒ [(x – 2) (x + 3)] = 14

Distribute the FOIL to get;

⇒ x ² – x – 6 = 14

⇒ x ² – x – 20 = 0

⇒ (x + 4) (x – 5) = 0

x = -4 or x = 5

when x = -5 and x = 5 are substituted in the original equation, they give a negative and positive argument respectively. Therefor, x = 5 is the only acceptable solution.

Example 9

Solve log ₃ x + log ₃ (x + 3) = log ₃ (2x + 6)

Solution

Given the equation; log ₃ (x² + 3x) = log ₃ (2x + 6), drop the logarithms to get;
⇒ x² + 3x = 2x + 6
⇒ x² + 3x – 2x – 6 = 0
x² + x – 6 = 0……………… (Quadratic equation)
Factor the quadratic equation to get;

(x – 2) (x + 3) = 0
x = 2 and x = -3

By verifying both values of x, we get x = 2 to be the correct answer.

Example 10

Solve log ₅ (30x – 10) – 2 = log ₅ (x + 6)

Solution

log ₅ (30x – 10) – 2 = log ₅ (x + 6)

This equation can be rewritten as;

⇒ log ₅ (30x – 10) –  log ₅ (x + 6) = 2

Simplify the logarithms

log ₅ [(30x – 10)/ (x + 6)] = 2

Rewrite logarithm in exponential form.

⇒ 5² = [(30x – 10)/ (x + 6)]

⇒ 25 = [(30x – 10)/ (x + 6)]

On cross multiplying, we get;

⇒ 30x – 10 = 25 (x + 6)

⇒ 30x – 10 = 25x + 150

⇒ 30x – 25x = 150 + 10

⇒ 5x = 160

x = 32