- Home
- >
- Squeeze theorem – Definition, Proof, and Examples
JUMP TO TOPIC
Squeeze theorem – Definition, Proof, and Examples
 Squeeze Theorem helps us evaluate complicated functions when all our fundamental techniques do not apply. Oscillating functions (normally containing trigonometric expressions), for example, will need another approach if we want to predict their end behavior at different points. This is when Squeeze Theorem can be most helpful.
Squeeze Theorem helps us evaluate complicated functions when all our fundamental techniques do not apply. Oscillating functions (normally containing trigonometric expressions), for example, will need another approach if we want to predict their end behavior at different points. This is when Squeeze Theorem can be most helpful.
Squeeze Theorem helps us find the limit of complicated functions by squeezing this function between two functions with simpler forms.
In this article, we’ll extensively cover Squeeze Theorem and learn the following:
- The derivation of Squeeze Theorem.
- Understanding when it applies.
- Applying the Squeeze Theorem in different examples.
This theorem is especially important when we’re working with functions resulting from multiplying different types of expressions (such as the product of a polynomial and a trigonometric expression).
We’ll also be applying Squeeze Theorem in advanced pre-Calculus and Calculus classes, so we should start early and master our knowledge on Squeeze Theorem.
Why don’t we begin by understanding the reasoning behind the name of this important theorem?
What is the Squeeze Theorem?
We’ll get into the more technical definition of Squeeze Theorem in the next section, but for now, let’s try to understand the concept behind its name.
Squeeze Theorem (or also known as the sandwich theorem) uses two functions to find the limit of the actual function we’re working on.
Let’s say we want to find the limit of $f(x)$ as $x$ approaches $a$, but the algebraic techniques that we learned in the past are not applicable.
What we can do instead is “squeeze” $f(x)$ between two other simpler functions, $g(x)$ and $h(x)$.
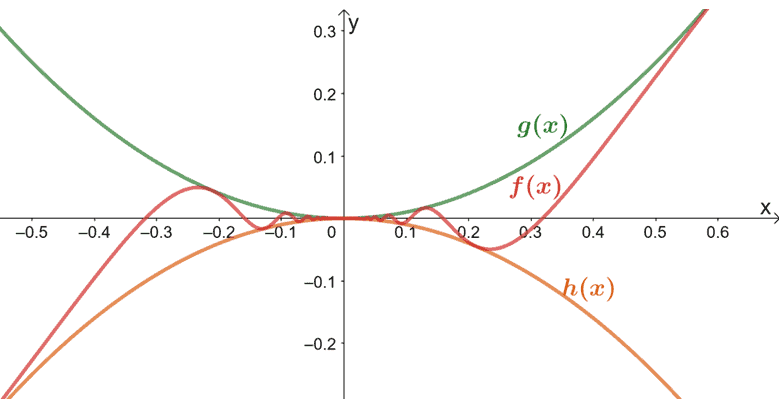
The graph, for example, shows us how $f(x) = x^2 \sin\left( \dfrac{1}{x} \right)$ can be sandwiched between two simpler functions such as $g(x) = x^2$ and $h(x) = -x^2$.
Why do we call them “simpler functions”? That’s because finding the limits of $g(x)$ and $h(x)$ are much easier since we can apply the techniques we’ve learned in the past. In the next sections, we’ll learn about the important conditions when choosing the best functions to sandwich the original function.
But focusing on what we know so far, we can see that the Squeeze Theorem actually lives up to its name – we’re squeezing our original function in between two other functions.
Formal Squeeze Theorem definition
We’ve discussed the Squeeze Theorem’s conceptual idea, but how do we define Squeeze Theorem mathematically?
Given the three functions, $f(x)$, $g(x)$, and $h(x)$ so that $g(x) \leq f(x) \leq h(x)$,
and in addition, when $\lim_{x \rightarrow a} g(x) = \lim_{x \rightarrow a} h(x) = L$,
we also have $\lim_{x \rightarrow a} f(x) = L$.
This means that when $f(x)$ is sandwiched between $g(x)$ and $h(x)$, and if the limit of $g(x)$ and $h(x)$ as $x$ approaches $a$ are both equal to a value,$L$, then the limit of $f(x)$ as $x$ approaches $a$ will also be equal to $L$.
Let’s say we have $-x^2 \leq f(x) \leq x^2$ and $\lim_{x \rightarrow 0} -x^2 = \lim_{x \rightarrow 0} x^2 = 0$, we can apply the Squeeze Theorem to conclude that $\lim_{x \rightarrow 0} f(x) = 0$.
Don’t worry. We’ll learn about this in the later section as well.
When to use Squeeze Theorem?
Keep in mind that we use the Squeeze Theorem when it seems impossible to evaluate the limit of the function using the algebraic techniques that we’ve discussed in this article.
- Squeeze Theorem is most helpful when finding the limit of functions that are oscillating (significant difference in values of $f(x)$ as $x$ varies and approaches infinity).
- This means Squeeze Theorem is helpful when working with complex trigonometric functions’ limits.
- Squeeze Theorem can also be used when it’s easy for us to think of two functions we can sandwich the function in.
These are just some of the functions that may require us to apply Squeeze Theorem to find their limits: $ \lim_{x \rightarrow 0} x^2 \sin \left(\dfrac{1}{x}\right)$ and $ \lim_{x \rightarrow 0} x^2 \cos \left(\dfrac{1}{x}\right)$.
How to use the Squeeze Theorem?
When we have a complicated function,$f(x)$, what we can do is cleverly think of two functions, $g(x)$ and $h(x)$ that satisfy the following conditions:
- The function $f(x)$ must also lie in between the two functions, $g(x) \leq f(x) \leq h(x)$.
- Both $ \lim_{x \rightarrow a} g(x)$ and $ \lim_{x \rightarrow a} g(x)$ are easy to evaluate.
- Confirm that $ \lim_{x \rightarrow a} g(x)$ = $ \lim_{x \rightarrow a} h(x)$.
Once we can confirm these, we can then equate the limit of either $g(x)$ or $h(x)$ to $ \lim_{x \rightarrow a} f(x)$. It helps if $f(x)$ or parts of it can be bound between to values, so finding $g(x)$ and $h(x)$ are much easier.
Here are some steps to remember when evaluating limits using the Squeeze Theorem.
- Start with an initial inequality you can work on.
- Modify this inequality so that the expression in the middle represents the function that we need.
- Evaluate the limits of the right and left ends of the inequalities.
- If they are equal, apply the Squeeze Theorem.
Let’s use the guide and Squeeze Theorem to evaluate $ \lim_{x \rightarrow 0} x^2 \cos \left(\dfrac{1}{x}\right)$.
- Recall that the value of $\cos \left(\dfrac{1}{x} \right)$ ranges between $-1$ and $1$, except when $x = 0$.
- Bound $\cos \left(\dfrac{1}{x} \right)$ between these two values.
- So that we have our original expression in the middle of the inequality, let’s multiply both sides of the inequality by $x^2$.
$\begin{aligned} -1 &\leq \cos\left(\dfrac{1}{x} \right ) \leq 1\\-1 \cdot {\color{blue}x^2} &\leq {\color{blue}x^2}\cdot \cos\left(\dfrac{1}{x} \right ) \leq 1\cdot {\color{blue}x^2}\\-x^2 &\leq x^2 \cos\left(\dfrac{1}{x} \right )\leq x^2 \end{aligned}$
We now have sandwiched our function in between $-x^2$ and $x^2$. Let’s go ahead and evaluate $ \lim_{x \rightarrow 0} -x^2$ and $ \lim_{x \rightarrow 0} x^2$.
This time, it will be easier for us to evaluate their limits since we can just substitute $x = 0$ into each of the expressions.
| $\begin{aligned}\lim_{x\rightarrow 0} -x^2 &= -(0)^2\\&=0 \end{aligned}$ | $\begin{aligned}\lim_{x\rightarrow 0} x^2 &= (0)^2\\&=0 \end{aligned}$ |
Since both the limits are equal to 0, by Squeeze Theorem, we can conclude that $ \lim_{x \rightarrow 0} x^2 \cos \left(\dfrac{1}{x}\right) = 0$.
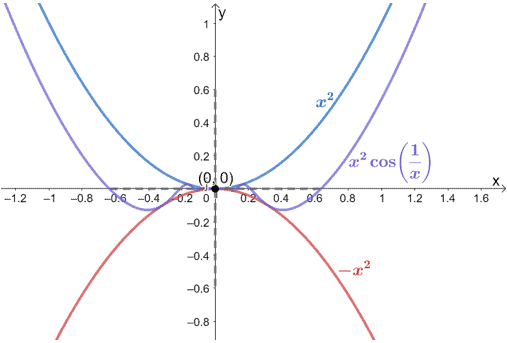
This graph also confirms two things:
- The function $ x^2 \cos \left(\dfrac{1}{x}\right)$ is sandwiched between the graphs of $x^2$ and $-x^2$
- They all share the same value as $x$ approaches $0$. Hence, $ \lim_{x \rightarrow 0} -x^2 = \lim_{x \rightarrow 0} x^2 = \lim_{x \rightarrow 0} x^2 \cos \left(\dfrac{1}{x}\right) = 0$.
From this example, we can also see how the algebraic techniques in evaluating limits are still important even for limits requiring the Squeeze Theorem. Make sure to review all these techniques as well.
Summary of Squeeze Theorem definition and properties
Before we wrap up this discussion, let’s review everything that we have learned so far.
- We can evaluate $\lim_{x \rightarrow a} f(x)$ by Squeeze Theorem only when $g(x) \leq f(x) \leq h(x)$ and $\lim_{x \rightarrow a} g(x) = \lim_{x \rightarrow a} h(x) = L$.
- When this happens, $\lim_{x \rightarrow a} f(x) = L$.
- It’s helpful to bound the expression of $f(x)$ or parts of $f(x)$ by a reasonable range or expression then manipulate the expressions to end up with the bounded expressions sharing the same limit.
Use the helpful guide we have prepared in the earlier section when evaluating limits using the Squeeze Theorem.

Make sure to also refresh your knowledge in evaluating limits as we need our previous knowledge for the third step.
That’s about it – but if you’re curious about how the Squeeze Theorem was derived, here’s a proof of the theorem so we can better understand it.
Additional knowledge: Squeeze Theorem proof
We can prove the Squeeze Theorem using the technical definition of limits.
Our assumptions are $\lim_{x \rightarrow a} g(x) = L$ and $\lim_{x \rightarrow a} h(x) = L$ and that $ g(x) \leq f(x) \leq h(x)$.
Let $\epsilon > 0$ and if we want $\lim_{x \rightarrow a} g(x)$ to also be equal to $L$, there should exist a $\delta_g$ that satisfies the condition below. If $0 < |x – a| < \delta_g$, $|g(x) – L| < \epsilon$ must also be true. Taking out the absolute expression, we will now have $-\epsilon < g(x) – L< \epsilon$.
Similarly, for $\lim_{x \rightarrow a} h(x)$, since this expression must be equal to $L$, there exists a $\delta_h$ so that when $0 < |x – a| < \delta_h$, $|h(x) – L| < \epsilon$. Removing the absolute value for this inequality, we also have $-\epsilon < h(x) – L< \epsilon$.
Let $\delta$ be the smaller between the two: $\delta_g$ and $\delta_h$. It can be shown that when $0 < |x – a|< \delta$, the inequality $|f(x) – L| < \epsilon$ must also be true.
We know that $-\epsilon < g(x) – L< \epsilon$ and given that $ g(x) \leq f(x)$, we have the following:
$\begin{aligned} g(x) &\leq f(x)\\g(x)-L &\leq f(x) – L \\ -\epsilon < g(x)-L&\leq f(x) – L \end{aligned}$
Extending this same thought process to $h(x)$ and knowing that $g(x) \leq h(x)$, we have
$ \begin{aligned} -\epsilon &< g(x)-L \leq f(x) – L\\-\epsilon &< g(x)-L \leq f(x) – L \leq h(x) – L <\epsilon \end{aligned}$
This means that $f(x) – L$ is within the range of $-\epsilon$ and $\epsilon$: $-\epsilon < f(x) – L< \epsilon$. Consequently, $|f(x) – L| < \epsilon$ and so, we have shown that $\lim_{x \rightarrow a} f(x) = L$.
This proof is important when you’re trying to prove limits using their formal definition. For now, let’s try a few more problems, so we can practice what we just learned and apply the Squeeze Theorem to evaluate different functions.
Example 1
Evaluate $\lim_{x \rightarrow 0} 2 + 2x^2 \sin \left(\dfrac{1}{x} \right)$ using the Squeeze Theorem.
Solution
We can start with the fact that $\sin \left(\dfrac{1}{x} \right)$’s value ranges between $-1$ and $1$.
$-1\leq \sin \left(\dfrac{1}{x} \right) \leq 1$
So that we end up with $2 + 2x^2 \sin \left(\dfrac{1}{x} \right)$ the middle of the inequality, we multiply both sides by 2 then add 2 on both sides.
$\begin{aligned}-1&\leq \sin \left(\dfrac{1}{x} \right) \leq 1\\-1 \cdot {\color{blue}2x^2}&\leq {\color{blue}2x^2} \cdot \sin \left(\dfrac{1}{x} \right) \leq 1\cdot {\color{blue}2x^2}\\-2x^2 + {\color{blue}2}&\leq{\color{blue}2} + 2x^2\sin \left(\dfrac{1}{x} \right) \leq 2x^2 + {\color{blue}2}\\-2x^2 +2 &\leq2 + 2x^2\sin \left(\dfrac{1}{x} \right) \leq 2x^2 + 2\end{aligned}$
We can see that $-2x^2 +2 \leq 2 + 2x^2\sin \left(\dfrac{1}{x} \right) \leq 2x^2 + 2$, so we can evaluate the limit of both sides of the inequality and compare the results.
| $\boldsymbol{-2x^2 + 2 }$ | $\boldsymbol{2x^2 + 2}$ |
| $\begin{aligned}\lim_{x\rightarrow 0} -2x^2 + 2 &= -2(0)^2 + 2\\&= 2 \end{aligned}$ | $\begin{aligned}\lim_{x\rightarrow 0} 2x^2 + 2 &= 2(0)^2 + 2\\&= 2 \end{aligned}$ |
We can see that both the limits of the expression are equal. If we have $f(x) = 2 + 2x^2 \sin \left(\dfrac{1}{x} \right)$, we can use $g(x) = -2x^2 + 2$ and $h(x) = 2x^2 + 2$ as the bounding functions.
Since, $\lim_{x \rightarrow 0} g(x) = \lim_{x \rightarrow 0} h(x) = 2$, and $f(x)$ is sandwiched between the two, by Squeeze Theorem, we have $\lim_{x \rightarrow 0} f(x) = 2$.
This means that $\lim_{x \rightarrow 0} 2 + 2x^2 \sin \left(\dfrac{1}{x} \right)$ is equal to $\boldsymbol{2}$.
Example 2
Evaluate $\lim_{x \rightarrow 0} x^2 e^{\sin \frac{1}{x}}$ using the Squeeze Theorem.
Solution
We can once again begin with the fact that $\sin \left(\dfrac{1}{x} \right)$’s value ranges between $-1$ and $1$.
$-1\leq \sin \left(\dfrac{1}{x} \right) \leq 1$
We can then raised both sides of the inequality by $e$.
$ {\color{blue}e}^{-1}\leq {\color{blue}e}^{\sin \frac{1}{x}} \leq {\color{blue}e}^1$
Multiply both sides of the inequality by $x^2$ after.
${\color{blue} x^2}e^{-1}\leq {\color{blue} x^2}e^{\sin \frac{1}{x}} \leq {\color{blue} x^2}e^1$
We now have our desired expression for the expression in the middle of the inequality.
Now that we have bounded our original function with two functions, $x^2 e^{-1}$ and $x^2 e^{1}$, we can evaluate the limits of each expression as $x$ approaches $0$.
| $\boldsymbol{ x^2 e^{-1} }$ | $\boldsymbol{ x^2 e^{1}}$ |
| $\begin{aligned}\lim_{x\rightarrow 0} x^2 e^{-1} &= (0)^2 e^{-1}\\&= 0 \end{aligned}$ | $\begin{aligned}\lim_{x\rightarrow 0} x^2 e^{1} &= (0)^2 e^{1}\\&= 0 \end{aligned}$ |
Since both of their limits are equal, we can use their limit to find $\lim_{x \rightarrow 0} x^2 e^{\sin \frac{1}{x}}$.
Recall that when a function is sandwiched between two functions, if the two functions’ limits are equal, then the sandwiched function will have the same limit.
Hence, we have $\lim_{x \rightarrow 0} x^2 e^{-1} =\lim_{x \rightarrow 0} x^2 e^{1} = \lim_{x \rightarrow 0} x^2 e^{\sin \frac{1}{x}} = \boldsymbol{0}$.
Example 3
Evaluate $\lim_{x \rightarrow \infty} \dfrac{2x(\cos x + \sin^3x)}{(x^4 + 1)(x – 6)}$ using the Squeeze Theorem.
Solution
We can start with the inequality, $-1 \leq \sin x \leq 1$ then modify this so we end up with $\dfrac{2x(\cos x + \sin^3x)}{(x^4 + 1)(x – 6)}$ in the middle of the inequality.
What we can do is cube both sides of the inequality.
$-1 \leq \sin^3 x \leq 1$
Note that we can add $-1 \leq \cos x \leq 1$ to our inequality. Hence, we now have the inequality shown below.
$-2 \leq \cos x + \sin^3 x \leq 2$
We’re near our ideal expression for the expression in the center of the inequality. Let’s go ahead and divide both ends of the inequality by $(x^4 + 1)(x – 6)$.
$\begin{aligned}-2 &\leq \cos x + \sin^3 x \leq 2\\\dfrac{-2}{(x^4 + 1)(x – 6)}&\leq \dfrac{\cos x + \sin^3 x}{(x^4 + 1)(x – 6)} \leq \dfrac{2}{(x^4 + 1)(x – 6)} \end{aligned}$
We have now successfully manipulated the inequality so that we have $\dfrac{2x(\cos x + \sin^3x)}{(x^4 + 1)(x – 6)}$ bounded between two functions: $\dfrac{-2}{(x^4 + 1)(x – 6)}$ and $\dfrac{2}{(x^4 + 1)(x – 6)}$.
Let’s go ahead and evaluate the limits of these two ends and see if they’re equal. When evaluating limits of a function as $x \rightarrow \infty$, let’s try to use $\lim_{x \rightarrow \infty} \dfrac{1}{x^n} = 0$ whenever possible.
To apply this in our expression, divide both numerator and denominator by $x^4$.
$\begin{aligned} \lim_{x \rightarrow \infty}\dfrac{-2}{(x^4 + 1)(x – 6)}&= \lim_{x \rightarrow \infty}\dfrac{\dfrac{-2}{\color{blue}x^4}}{\left(\dfrac{x^4}{{\color{blue}x^4}} + \dfrac{1}{{\color{blue}x^4}}\right)\left(\dfrac{x}{{\color{blue}x^4}} – \dfrac{6}{{\color{blue}x^4}}\right)}\\&= \lim_{x \rightarrow \infty} \dfrac{ -\dfrac{2}{x^4}}{\left(1+ \dfrac{1}{x^4} \right )\left(1- \dfrac{6}{x^4} \right )}\\&= \dfrac{\lim_{x \rightarrow \infty} -\dfrac{2}{x^4}}{\lim_{x \rightarrow \infty}\left(1+ \dfrac{1}{x^4} \right )\left(1- \dfrac{6}{x^4} \right )} \\&= \dfrac{\color{blue}0}{(1+ {\color{blue}0})(1-{\color{blue}0})}\\&=0\end{aligned}$
We can apply the same process for the right-hand expression, $\dfrac{2}{(x^4 + 1)(x – 6)}$.
$\begin{aligned} \lim_{x \rightarrow \infty}\dfrac{2}{(x^4 + 1)(x – 6)}&= \lim_{x \rightarrow \infty}\dfrac{\dfrac{2}{\color{blue}x^4}}{\left(\dfrac{x^4}{{\color{blue}x^4}} + \dfrac{1}{{\color{blue}x^4}}\right)\left(\dfrac{x}{{\color{blue}x^4}} – \dfrac{6}{{\color{blue}x^4}}\right)}\\&= \lim_{x \rightarrow \infty} \dfrac{ \dfrac{2}{x^4}}{\left(1+ \dfrac{1}{x^4} \right )\left(1- \dfrac{6}{x^4} \right )}\\&=0\end{aligned}$
From this, we can see that $\dfrac{-2}{(x^4 + 1)(x – 6)} = \dfrac{2}{(x^4 + 1)(x – 6)} = 0$.
Since these are the two expressions bounding $\dfrac{2x(\cos x + \sin^3x)}{(x^4 + 1)(x – 6)}$ and the limits of the bounds are equal, we can apply the Squeeze Theorem.
Hence, we have $\lim_{x \rightarrow \infty} \dfrac{2x(\cos x + \sin^3x)}{(x^4 + 1)(x – 6)}$ is equal to $\boldsymbol{0}$.
Images/mathematical drawings are created with GeoGebra.
Previous Lesson | Main Page | Next Lesson
Practice Questions
![]()
Open Problem
If $\lim_{x \rightarrow 0} x^3 = 0$ and $\lim_{x \rightarrow 0} x^7 = 0$, use the Squeeze Theorem to prove that $\lim_{x \rightarrow 0} x^5 = 0$.
Open Problem Solution
$\begin{aligned}x^3 \leq x^5 \leq x^7\\\lim_{x\rightarrow 0} x^3 =\lim_{x\rightarrow 0} x^7 =0\\\Rightarrow \lim_{x\rightarrow 0} x^5 =0\end{aligned}$
Images/mathematical drawings are created with GeoGebra.
