- Home
- >
- Law of Cosines – Explanation & Examples
Law of Cosines – Explanation & Examples
We already know we can determine the unknown parts (sides and angles) of any type of triangles using the Law of Sines. However, this has certain shortfalls as we can’t use it unless we have specific combinations of angles and sides to solve the triangle. This is where the Law of Cosines comes in.
The Law of Cosines helps us determine the missing parts of any triangle if we know the measure of two sides of a triangle and the angle between them. It simply relates the lengths of the legs of any triangle to the cosines of one of its angles.
In this lesson, we will learn the concepts driven by the following questions and be qualified to address them and get accurate and consistent answers.
- What is the Law of Cosines?
- When to use the Law of Cosines?
- How can we use the Law of Cosines?
What Is Law of Cosines?
The Law of Cosines is the relationship between the legs of any triangle to the cosines of one of its angles. This law helps us determine the missing parts of any triangle if we know the measure of two sides of a triangle and the angle between them.
Consider a triangle $△ABC$ with the sides $a$, $b$, and $c$ facing the angles $\alpha$, $\beta$, and $\gamma$ respectively as shown in Figure 14-1.

Note that the side ${\displaystyle {\overline {AC}}}$ of the triangle is along the positive direction of the x-axis with vertex $A$ at the origin, so $∠BAC$ is in the standard position. Thus,
${\displaystyle {\overline {AB}}} = c$
$m∠BAC = \alpha$
Therefore, the coordinates of the point $B$ will be $(c \cos \alpha, c \sin \alpha)%%EDITORCONTENT%%nbsp;
Also
$AC = b$ and point $C$ lies on the x-axis, so
The coordinates of the point $C$ will be $(b, 0)$
By distance formula
$|{\displaystyle {\overline {BC}}}|\:=\:\left(c\:\cos\: \alpha-b\right)^2+\left(c\:\sin\: \alpha-0\right)^2$
$a^2\:=\:c^2\:\cos^2\:\alpha\:+b^2\:-\:2bc\:\cos\:\alpha\:+\:c^2\:\sin^2\:\alpha%%EDITORCONTENT%%nbsp; ∵ ${\displaystyle {\overline {BC}}} = a$
$a^2\:=\:c^2\:\left(\cos^2\:\alpha+\sin^2\:\alpha\right)+b^2\:-\:2bc\:\cos\:\alpha\:\:$
$a^2\:=\:c^2\:\left(1\right)+b^2\:-\:2bc\:\cos\:\alpha%%EDITORCONTENT%%nbsp; ∵ $\cos^2\:\alpha\:+\:\sin^2\:\alpha\:=\:1$
$a^2\:=\:b^2\:+c^2\:-\:2bc\:\cos\:\alpha%%EDITORCONTENT%%nbsp; $— [1]$
Similarly, we can determine
$b^2\:=\:c^2\:+a^2\:-\:2ca\:\cos\:\beta%%EDITORCONTENT%%nbsp; $— [2]$
$c^2\:=\:a^2\:+b^2\:-\:2ab\:\cos\:\gamma%%EDITORCONTENT%%nbsp; $— [3]$
The equations $[1]$, $[2]$, and $[3]$ are known as the Law of Cosines.
Therefore, the Law of Cosines states that the square of the measure of one side of a triangle is equal to the sum of the squares of the other two sides minus twice times the measures of those two sides times the cosine of the angle between them.
It is important to note that the Law of Cosines would reduce to Pythagoras Theorem if $△ABC$ is a right-angled triangle such as:
If
$\alpha = 90^{\circ }$, $\beta = 90^{\circ }$ and $\gamma = 90^{\circ }$ respectively
then
$a^2\:=\:b^2\:+c^2\:-\:2bc\:\cos\:\alpha$ would be $a^2\:=\:b^2\:+c^2%%EDITORCONTENT%%nbsp; ∵ $\cos 90^{\circ } = 0$
$b^2\:=\:c^2\:+a^2\:-\:2ca\:\cos\:\beta$ would be $b^2\:=\:c^2\:+a^2%%EDITORCONTENT%%nbsp; ∵ $\cos 90^{\circ } = 0$
$c^2\:=\:a^2\:+b^2\:-\:2ab\:\cos\:\gamma$ would be $c^2\:=\:a^2\:+b^2%%EDITORCONTENT%%nbsp; ∵ $\cos 90^{\circ } = 0$
In a nutshell, the Law of Cosines simply generalizes the Pythagoras theorem.
The only difference between the Law of Cosines and the Pythagoras theorem is that the Pythagoras theorem is applicable for right-angled triangles and the Law of Cosines holds for any triangle.
When to Use Law of Cosines?
We can use the Law of Cosines when we are given two sides and the included angle to determine a missing side, when we are given three sides to determine a missing angle, or when we are given two sides and the non-included angle to determine a missing side.
We already determined that if a triangle $△ABC$ with the sides $a$, $b$, and $c$ facing the angles $\alpha$, $\beta$, and $\gamma$ respectively, then:
$a^2\:=\:b^2\:+c^2\:-\:2bc\:\cos\:\alpha$
It indicates that the Law of Cosines works with only three legs and one angle at a time, thus we can apply the Law of Sines only if the following conditions are met.
- When we are given two sides and the included angle to determine a missing side — SAS.
- When we are given three sides to determine a missing angle — SSS.
- When we are given two sides and the non-included angle to determine a missing side — SSA.
Take note that the third condition is known as the Ambiguous case and we will explain it in detail in one of our future Trigonometry lessons.
We will only discuss the first two conditions for the moment.
How To Use Law of Cosines
The following examples will help us determine how we can use the Law of Cosines.
When two sides and the included angle is given
Example 1
In triangle $△ABC$, $m∠A = 52^{\circ }$, $b = 9.5$ and $c = 3.4$. What is the length of side $a$?

Solution:
By law of cosines, we have
$a^2\:=\:b^2\:+c^2\:-\:2bc\:\cos\:\alpha$
substituting $b = 9.5$, $c = 3.4$ and $m∠A = 52^{\circ }$ in the formula
$a^2\:=\:(9.5)^2\:+(3.4)^2\:-\:2(9.5)(3.4)\:\cos\:52^{\circ }$
$a^2 = 90.25 + 11.56\: – 39.7717313$
$a^2 = 62.0382687$
$a ≈ 7.9$ units
Thus, the length of side $a$ is approximately $7.9$ units.
When three sides are given
Examples 2
In triangle $△ABC$, $a = 1.1$, $b = 2$ and $c = 1.6$. Determine the measure of the angle $A$ to the nearest integer?

Solution:
By law of cosines, we have
$a^2\:=\:b^2\:+c^2\:-\:2bc\:\cos\:\alpha$
$\cos\:A\:=\:\frac{b^2\:+\:c^2\:-\:a^2}{2bc}$
substituting $a = 1.1$, $b = 2$, and $c = 1.6$ in the formula
$\cos\:A\:=\:\frac{(2)^2\:+\:(1.6)^2\:-\:(1.1)^2}{2(2)(1.6)}$
$\cos\:A\:=\:\frac{4\:+\:2.56\:-\:1.21}{6.4}$
$\cos\:A\:= 0.8359375$
$A = arc cos (0.8359375)$
$A = 33.28641^{\circ }$
$A ≈ 33^{\circ }$
Therefore, the measure of angle $A$ is $33^{\circ }$.
Examples 3
Let $AC$ and $BC$ be the two forces of $F_1=\:400\:N$ and $F_2=\:300\:N$, respectively, which are inclined at an angle of $147^{\circ }$. Determine $AB$, the resultant of $AC$ and $BC$.
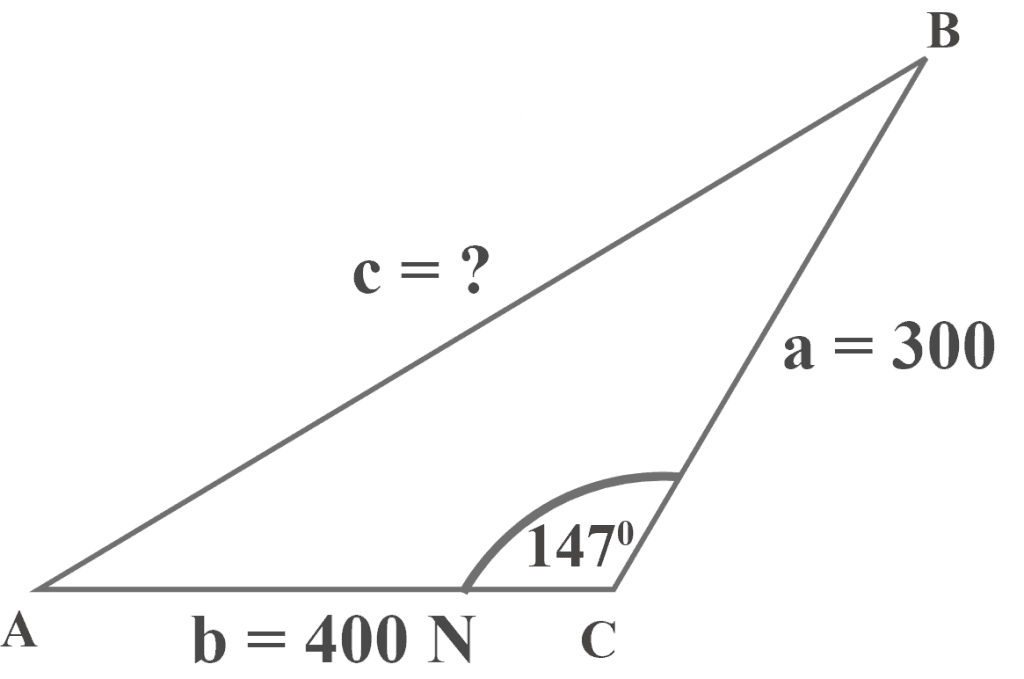
Solution:
Given
$b = AC = F_1=\:400\:N$
$a = BC = F_2=\:300\:N$
$m∠C = 147^{\circ }$
To determine
$AC = ?$
By law of cosines, we have
$c^2\:=\:a^2\:+b^2\:-\:2ab\:\cos C$
substituting $a = 300$, $b = 400$ and $m∠C = 147^{\circ }$ in the formula
$c^2\:=\:a^2\:+b^2\:-\:2ab\:\cos C$
$c^2\:=\:(300)^2\:+(400)^2\:-\:2(300)(400)\:\cos 147^{\circ }$
$c^2\:= 90000 + 160000\:– 2 (300) (400) (–0.83867057)$
$c^2\:= 250000 + 201280.936$
$c^2\:= 451280.936$
$c = 671.774468$
$c ≈ 671.77 N$ (Rounded to the hundredths place)
as
$c = AC$
so
$AC = 671.77 N$
Therefore, the resultant of $AC$ and $BC$ is approximately $671.77 N$.
