Trigonometry angles – Explanation & Examples 

In trigonometry, we often come across situations when we have to find the measure of certain trigonometry angles to solve the real word problems. We already know the three main evergreen trigonometric functions – sin, cosine, and tangent. We can find the length of any missing side if we know the length of one side and an angle measure. They simply receive angles as input and return the side ratios. But, what if you need to find the measure of an angle. Do you feel stuck?

Don’t worry! We just need functions that could ‘undo’ the trigonometric functions. We need inverse functions that receive side ratios as input and return the angles. Yeah, that’s it!

Trigonometry angles can be measured using trigonometry to solve real-world problems. In the context of a right-angled triangle, we can determine any missing angle if we know the length of the two sides of the triangle.

After studying this lesson, we are expected to learn the concepts driven by these questions and be qualified to address accurate, specific, and consistent answers to these questions.

• How do you find an angle using trigonometry?
• The role of inverse trigonometric functions to find the missing angle in a right-angled triangle.
• How can we solve actual problems using regular trigonometric functions and their inverses?

The goal of this lesson is to clear up any confusion you might have about finding the unknown angles in a right-angled triangle.

How do you find an angle using trigonometry?

In figure 6-1, a stair is placed $1$ meter away from the base of a wall. The length of the stair is $2$ meters. We need to know the following four-step method to determine the measure of an angle formed by the ladder and the ground.

Step 1 of 4

Determine the names of the two sides of a right-angled triangle we know

We know that in a right triangle, the terms opposite, adjacent, and hypotenuse are called the lengths of sides. In Figure 6-2, a typical triangle with the reference angle $\theta$ is shown.

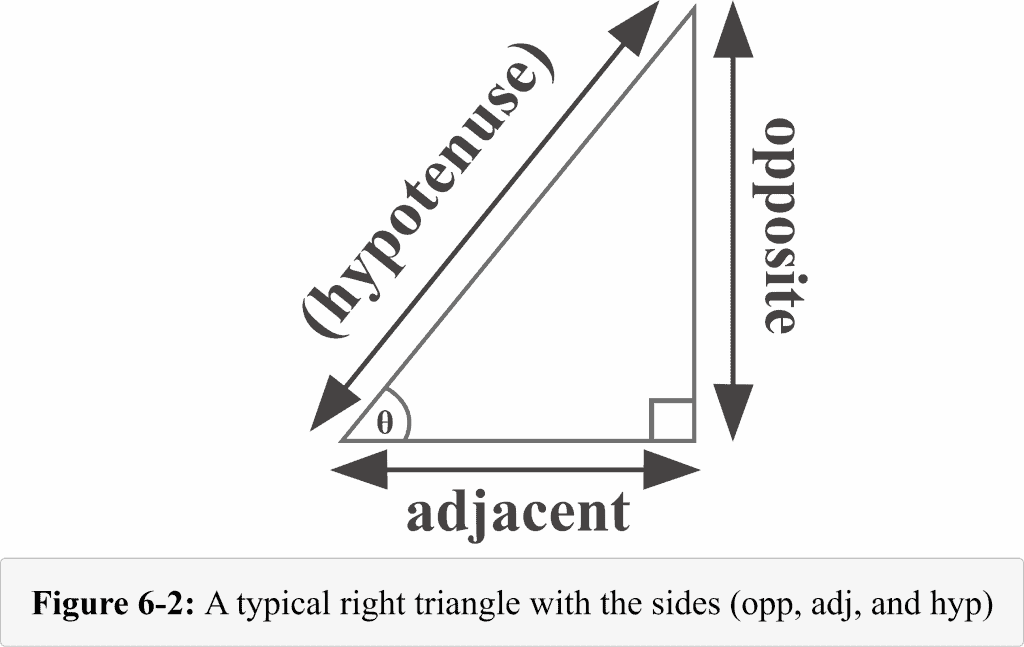
In our stair example, the side of length $1$ m is the adjacent side that lies right next to the reference angle $\theta$, and the side of length $2$ m is the hypotenuse. Thus,

Adjacent = $1$ m

Hypotenuse = $2$ m

Step 2 of 4

Determine and chose the appropriate type of trigonometric function (Out of sine, cos, and tan) based on the two sides we have

In our case, we have identified adjacent and opposite sides, indicating we need to use the Cosine function as shown in Figure 6-3.

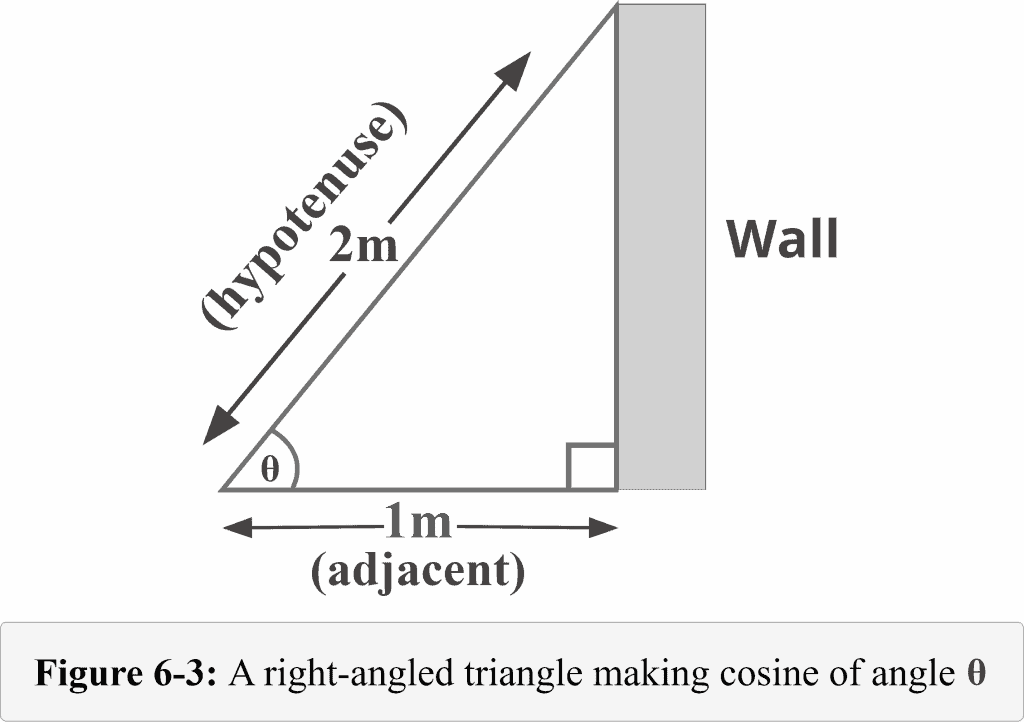
Step 3 of 4

Substituting the values in the appropriate function (In our case, it is cosine function)

We know that that the cosine function is the ratio of the adjacent side to the hypotenuse. Thus, using the formula

${\displaystyle \cos \theta ={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}}$

substitute adjacent = $1$, and hypotenuse = $2$ in the formula

${\displaystyle \cos \theta ={\frac {1}{2}}}$

$\cos \theta = 0.5$

Step 4 of 4

Solve the equation

$\cos \theta = 0.5$

$\theta =\cos^{-1}(0.5)$

Just get the calculator, enter $0.5$ and use the $\cos^{-1}$ button to determine the answer.

$\theta = 60^{\circ }$

Therefore, we conclude that the measure of an angle formed by the ladder and the ground is:

But, what does $\cos^{-1}$ indicate?

 The cosine function ‘cos‘ just receives an angle and returns the ratio ‘${\frac {\mathrm {adjacent}}{\mathrm {hypotenuse}}}$’.

But $\cos^{-1}$ just does the opposite.  It receives the ratio ‘${\frac {\mathrm {adjacent}}{\mathrm {hypotenuse}}}$’ and returns an angle.

Check the illustration in Figure 6-4.

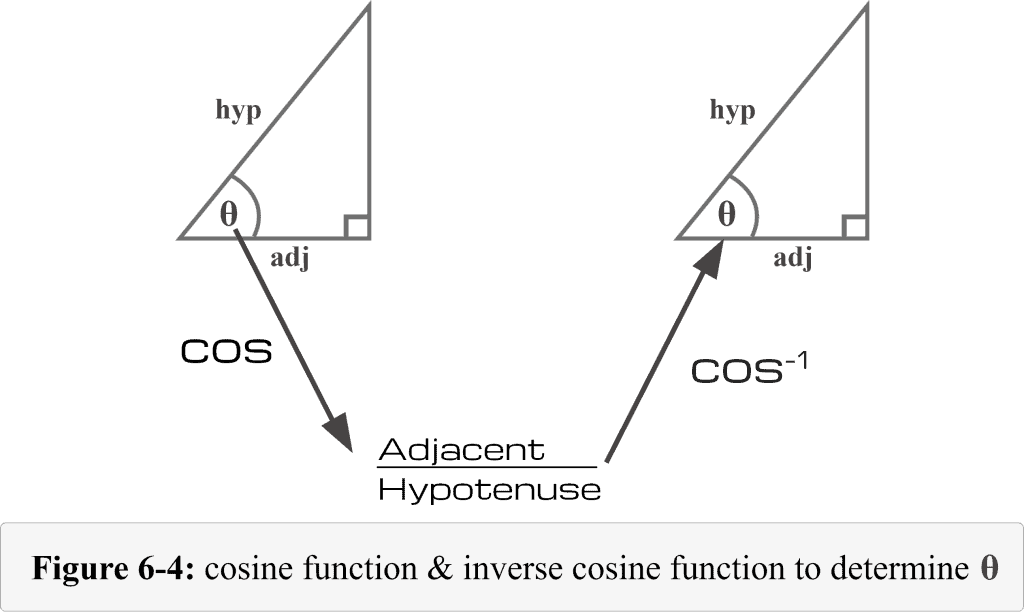
In a nutshell,

$\cos \theta = 0.5$

$\cos^{-1}(0.5) = 60^{\circ }$

Determining the angle using the sine function

What if we are asked to use the sine function to determine the angle formed by the ladder and the ground?

Well, it is very simple. We know that the sine function is the ratio of the opposite side to the hypotenuse. As the length of the opposite side is missing, so first we need to determine the missing side first.

Use the Pythagoras theorem,

$c^{2}=a^{2}+b^{2}$

Again considering the diagram 6-1, we have:

Adjacent $b = 1$

Hypotenuse $c = 2$

Opposite $a =$?

Substitute $b = 1$ and $c = 2$ in the formula 

$2^{2}=a^{2}+1^{2}$

$4=a^{2} + 1$

$a^{2} = 3$

$a = \sqrt{3 }$

Thus, the length of the opposite side is $\sqrt{3 }$ units.

Now, we have:

Opposite $a = \sqrt{3 }$

Hypotenuse $c = 2$

Using the formula of the sine function

${\displaystyle \sin \theta ={\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}}$

substitute opposite = $\sqrt{3 }$, and hypotenuse = $2$ in the formula

${\displaystyle \sin \theta ={\frac {\sqrt{3 }}{2}}}$

solving the equation

$\theta =\sin^{-1}{\frac {\sqrt{3 }}{2}}$

We know that $\sin^{-1}{\frac {\sqrt{3 }}{2}} = 60^{\circ }$

You can again check the calculator to verify.

Therefore, the measure of angle $\theta$ is:

Determining the angle using the tangent function

We know that the tangent function is the ratio of the opposite side to the adjacent side

Again considering diagram 6-1, we have:

Opposite = $\sqrt{3 }$

Adjacent = $1$

Using the formula of the tangent function

${\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

substitute opposite = $\sqrt{3 }$, and adjacent = $1$ in the formula

${\displaystyle \tan \theta ={\frac {\sqrt{3 }}{1}}}$

solving the equation

$\theta =\tan^{-1}(\sqrt{3 })$

We know that $\tan^{-1}(\sqrt{3 }) = 60^{\circ }$

You can again check the calculator to verify.

Therefore, the measure of angle $\theta$ is:

Therefore, we conclude that we can determine any missing angle of a right-angled triangle using any trigonometric function depending upon the sides of the right triangle we have.

We know that $\tan^{-1}(\sqrt{3 }) = 60^{\circ }$

You can again check the calculator to verify.

Therefore, the measure of angle $\theta$ is:

Therefore, we conclude that we can determine any missing angle of a right-angled triangle using any trigonometric function depending upon the sides of the right triangle we have.

Example $1$

Given a right-angled triangle with the reference angle $\alpha$. What is the angle $\alpha$?

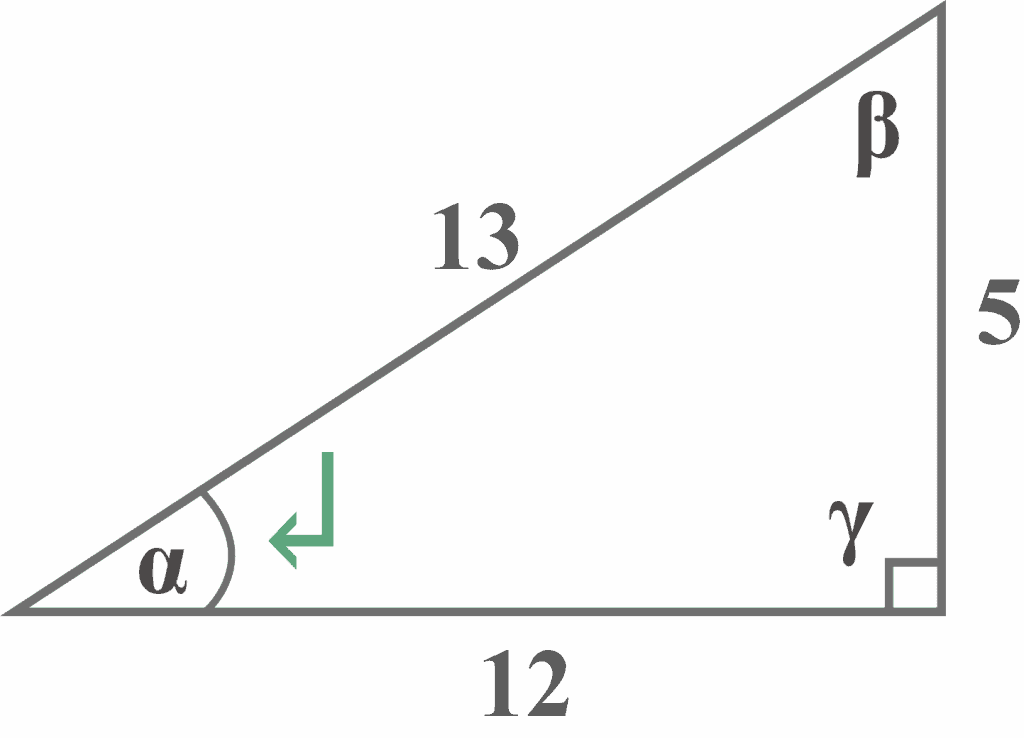
Solution:

Looking at the diagram, it is clear that the side of length $12$ is the adjacent side that lies right next to the reference angle α, and the side of length $5$ is the opposite side that lies exactly opposite the reference angle $\alpha$.

Adjacent = $12$

Opposite = $5$

We know that the tangent function is the ratio of the opposite side to the adjacent side.

${\displaystyle \tan \alpha ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

substitute opposite = $5$, and adjacent = $12$ in the formula

${\displaystyle \tan \alpha ={\frac {5}{2}}}$

$\tan \alpha = 0.41666667$

$\alpha =\tan^{-1}(0.41666667)$

Just get the calculator, enter $0.5$ and use the $\cos^{-1}$ button to determine the answer.

$\theta \approx 22.6^{\circ }$

Therefore, the measure of angle $\alpha$ is:

Please note that we could have also used the sine or cosine function as the right triangle in the diagram shows the lengths of all the sides.

Example $2$

Given a right-angled triangle with the reference angle $\beta$. What is the angle $\beta$?

Solution:

Looking at the diagram, it is clear that

Adjacent = $5$

Hypotenuse = $13$

Thus, the appropriate function to determine the angle $\beta$ should be the cosine function.

Using the formula of the cosine function

${\displaystyle \cos \beta ={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}}$

substitute adjacent = $5$, and hypotenuse = $13$ in the formula

${\displaystyle \cos \beta ={\frac {5}{13}}}$

$\cos \beta = 0.38461538$

$\beta =\cos^{-1}(0.38461538)$

$\beta \approx 67.4^{\circ }$

Therefore, the measure of angle $\alpha$ is:

Example $3$

Given a right-angled triangle with the reference angle $\alpha$. What is the angle $\alpha$?

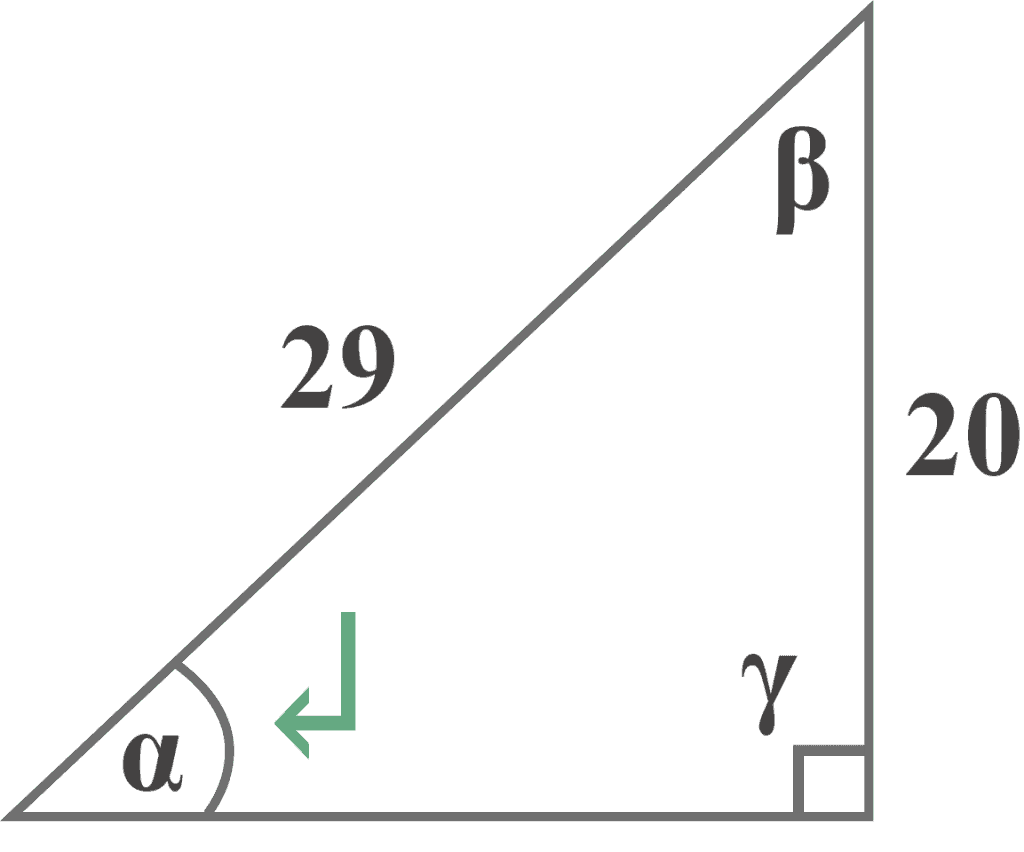
Solution:

Looking at the diagram, it is clear that

Opposite = $20$

Hypotenuse = $29$

Thus, the appropriate function to determine the angle α should be the sine function.

Using the formula of the sine function

${\displaystyle \sin \alpha ={\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}}$

substitute opposite = $20$, and hypotenuse = $29$ in the formula

${\displaystyle \sin \alpha ={\frac {20}{29}}}$

$\sin \alpha = 0.68965517$

$\alpha =\sin^{-1}(0.68965517)$

$\alpha \approx 43.6^{\circ }$

Therefore, the measure of angle $\alpha$ is:

Example $4$

Given a right-angled triangle with the sides $3$ and $4$. Determine: 

       a) The measure of angle $\alpha$ (using tangent function)

       b) The measure of angle $\beta$ (using sine or cosine function)

       c) Prove that $\alpha + \beta + \gamma = 180^{\circ }$

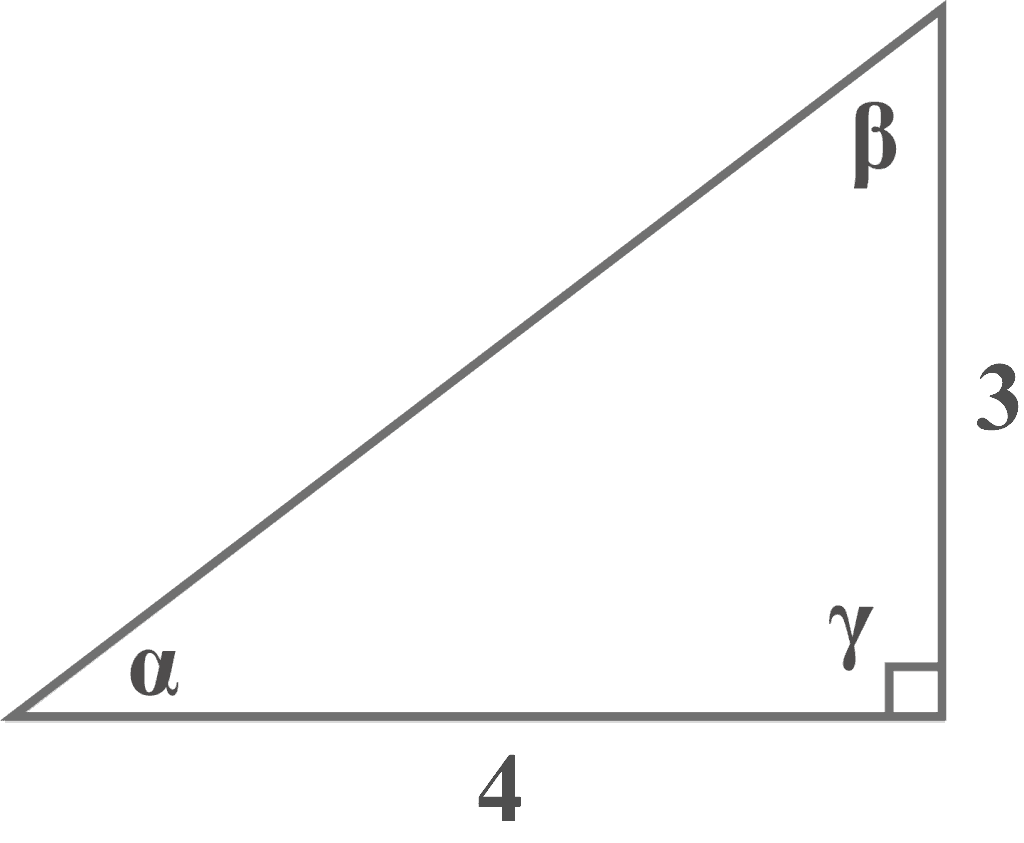Solution:

Part a: Determining the measure of angle $\alpha$

Looking at the diagram from the perspective of the angle $\alpha$, we have

Opposite = $3$

Adjacent = $4$

Thus, the appropriate function to determine the angle $\alpha$ should be the tangent function.

Using the formula of the tangent function

${\displaystyle \tan \alpha ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

substitute opposite = $3$, and adjacent = $4$ in the formula

${\displaystyle \tan \alpha ={\frac {3}{4}}}$

$\tan \alpha = 0.75$

$\alpha =\tan^{-1}(0.75)$

$\alpha \approx 36.9^{\circ }$

Therefore, the measure of angle $\alpha$ is:

Part b: Determining the measure of angle $\beta$

As we have to use either cosine function or sine function to determine the measure of angle $\beta$.

Since both the cosine or sine functions involve hypotenuse, but here hypotenuse is missing.

Thus, first we need to determine the hypotenuse before choosing any of these functions.

Use the Pythagoras theorem to determine the hypotenuse $c$

$c^{2}=a^{2}+b^{2}$

We have:

$a = 3$

$b = 4$

substitute $a = 3$ and $b = 4$ in the formula

$c^{2}=3^{2}+4^{2}$

$c^{2}=9+16$

$c^{2}=25$

$c = 5$ units

Thus, the length of the hypotenuse is $5$ units.

Now, with the perspective of angle $\beta$, we have:

Adjacent = $3$

Opposite = $4$

Hypotenuse = $5$

Let us chose cosine function to determine the angle $\beta$.

Using the formula of the cosine function

${\displaystyle \cos \beta ={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}}$

substitute adjacent = $3$, and hypotenuse = $5$ in the formula

${\displaystyle \cos \beta ={\frac {3}{5}}}$

$\cos \beta = 0.6$

$\beta =\cos^{-1}(0.6)$

$\beta \approx 53.1^{\circ }$

Therefore, the measure of angle $\beta$ is:

Part c: Proving that $\alpha + \beta + \gamma = 180^{\circ }$

Looking at the diagram, tiny square with the angle $\gamma$ shows that it is a right angle. Thus,

$\gamma = 90^{\circ }$

In previous parts, we determined that:

$\alpha = 36.9^{\circ }$

$\beta = 53.1^{\circ }$

Using the formula,

$\alpha + \beta + \gamma = 180^{\circ }$

substituting $\alpha = 36.9^{\circ }$, $\beta = 53.1^{\circ }$ and $\gamma = 90^{\circ }$ in the formula

$36.9^{\circ } + 53.1^{\circ } + 90^{\circ } = 180^{\circ }$

$90^{\circ } + 90^{\circ } = 180^{\circ }$

$180^{\circ } = 180^{\circ }$

L.H.S = R.H.S

Therefore, we proved that the sum of angles in a triangle is always 180^{\circ }.