- Home
- >
- Triple Integral – Definition, General Forms, and Examples
JUMP TO TOPIC
Triple Integral – Definition, General Forms, and Examples
Through triple integrals, we can now extend our understanding of iterated integrals to expressions and functions with three variables. We can use triple integrals to calculate the volume and mass of different objects – which are important components we need in physics, structural engineering, and other fields. This is why understanding triple integrals are important if we want to work with setups where there are now three variables components.
Triple integrals represent the iterated of functions with three variables, $\boldsymbol{f(x, y, z)}$. Instead of integrating our function over a given area, we’re now integrating it over a three-dimensional figure that has volume.
At this point, it is important that you are familiar with how we set up and evaluate iterated and double integrals. Open the embedded links in a separate tab or window in case you need an immediate refresher.
Through this article, we’ll show you how we can visualize and understand what triple integrals represent. We’ll also provide a thorough explanation of how to evaluate different triple integrals. By the end of the discussion, you should also learn how to solve problems that involve triple integrals.
Are you ready?
Let’s begin by visualizing triple integrals in three-dimensional coordinate systems then use these representations to define them.
What Is a Triple Integral?
A triple integral is an iterated integral with three variables and over a three-dimensional region. We can treat triple integrals’ definition as an extension of that of the double integrals, but this time, we’re integrating over a volume instead of an area.
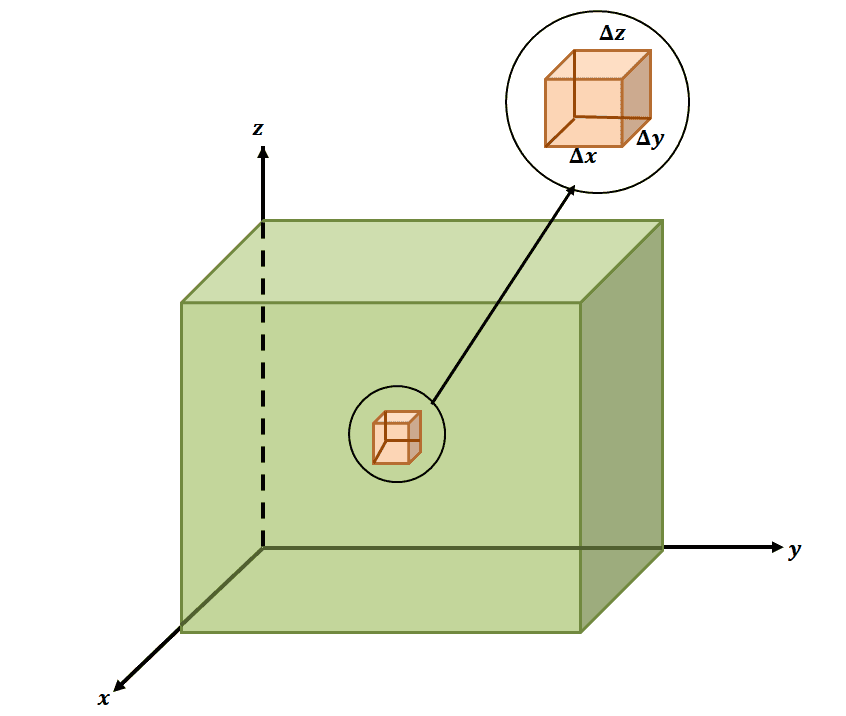
Similar to double integrals, we can start with a simple triple integral: divide the rectangular space into smaller boxes with the following dimensions: $\Delta x \times \Delta y \times \Delta z$. Adding the volume up and taking the volume’s limit will return the triple integral shown below:
\begin{aligned}\int \int \int_{S} f(x, y, z) \phantom{x} dV\end{aligned}
Keep in mind that for the triple integral to exist for the region $S$, $f(x,y , z)$ must be continuous and integrable on $S$. Let’s say we are integrating over the box with the following bounds:
\begin{aligned}S &= [a, b] \times [c, d] \times, [m, n] \end{aligned}
For this case, $[a, b]$ represents the limits with respect to $x$, $[c, d]$ are the limits for $y$, and $[m, n]$ are the limits for $z$. We can write the triple integral of $f(x, y, z)$ bounded by the box, $S$, as shown below.
\begin{aligned}\int \int \int_{S} f(x, y, z) \phantom{x} dV &= \int_{m}^{n} \int_{c}^{d} \int_{a}^{b} f(x, y, z) \phantom{x} dxdydz \end{aligned}
This is the common form that we’ll encounter when working with triple integrals, but there are six possible forms for triple integrals, in general. Now, let’s see how the expression for the triple integral changes when we’re working with more complex regions such as the one shown below.
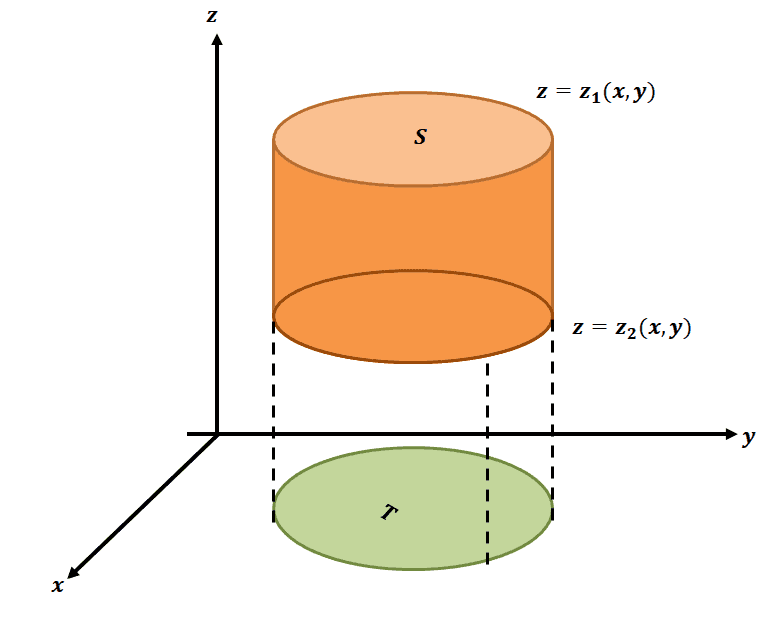
Suppose that we’re now integrating the function over a general region, $S$. The image above shows a region, $S$, in space and parallel to the $z$-axis. This region is bounded by the region shown as $T$ and is projection of $S$ onto the $xy$-plane.
\begin{aligned}T &= \{(x, y, z) | (x, y) \in T, z_1(x, y) \leq z \leq z_2(x, y)\}\end{aligned}
This notation highlights the conditions for $S$ and $T$ as well as the limits of integration for $z$ defined by the two other variables: $x$ and $y$. We use these limits to define the triple integral of $f(x, y, z)$ over the space, $S$.
\begin{aligned}\int \int \int_S f(x, y, z) \phantom{x} dV &= \int \int \int_{z_1(x, y)}^{z_2(x, y)} \phantom{x} dA\end{aligned}
As we have learned in the past, we integrate the remaining double integral over $dA$ by integrating with respect to $x$ then $y$. Hence, we have the following:
\begin{aligned}\int \int \int_S f(x, y, z) \phantom{x} dV &= \int_{z_1}^{z_2} \int_{y_1(z)}^{y_2(z)} \int_{z_1(x, y)}^{z_2(x, y)} \phantom{x} dA\end{aligned}
There are two other possible three-dimensional figures that may encounter when working with triple integrals: the space that has a projected region on the $xz$-plane and the space that can be projection on the $yz$-plane.
\begin{aligned}\boldsymbol{xz}\textbf{-plane} &: \{S = {(x, z) \in T, y_1(x, z) \leq y_2(x, z)}\}\\\boldsymbol{yz}\textbf{-plane} &: \{S = {(y, z) \in T, x_1(y, z) \leq x_2(y, z)}\}\end{aligned}
We’re now working with three variables where we project over a two-dimensional figure each time. This means that we’re expecting six possible iterated integrals in Cartesian form and we can find all six combinations by switching the places of $dx$, $dy$, and $dz$.
| Order of Integration | Triple Integral | Order of Integration | Triple Integral |
| $x \rightarrow y \rightarrow z$ | $\int_{z_1}^{z_2} \int_{y_1(z)}^{y_2(z)}\int_{x_1(y, z)}^{x_2(y, z)} f(x, y, z)\phantom{x}dx dy dz$ | $y \rightarrow z \rightarrow x$ | $\int_{x_1}^{x_2} \int_{z_1(x)}^{z_2(x)}\int_{y_1(x, y)}^{y_2(x, y)} f(x, y, z)\phantom{x}dx dy dz$ |
| $x \rightarrow z \rightarrow y$ | $\int_{y_1}^{y_2} \int_{z_1(y)}^{z_2(y)}\int_{x_1(y, z)}^{x_2(y, z)} f(x, y, z)\phantom{x}dx dz dy$ | $z \rightarrow x \rightarrow y$ | $\int_{z_1}^{z_2} \int_{x_1(z)}^{x_2(z)}\int_{y_1(x, z)}^{y_2(x, z)} f(x, y, z)\phantom{x}dx dz dy$ |
| $y \rightarrow x \rightarrow z$ | $\int_{z_1}^{z_2} \int_{x_1(z)}^{x_2(z)}\int_{y_1(x, z)}^{y_2(x, z)} f(x, y, z)\phantom{x}dy dx dz$ | $z \rightarrow y \rightarrow x$ | $\int_{x_1}^{x_2} \int_{y_1(x)}^{y_2(x)}\int_{z_1(x, z)}^{z_2(x, z)} f(x, y, z)\phantom{x}dy dx dz$ |
Let’s break down the first triple integral shown in this table to help you better understand how we define triple integrals.
\begin{aligned}\int_{z_1}^{z_2} \underbrace{\int_{y_1(z)}^{y_2(z)}\overbrace{\int_{x_1(y, z)}^{x_2(y, z)} f(x, y, z)\phantom{x}dx}^{^{\displaystyle{\text{Resulting function is in terms of $y$ and $z$}}}}dy}_{^{\displaystyle{\text{Resulting function is in terms of $z$}}}}dz\end{aligned}
Similar to double integrals, the bounds of the innermost integral are defined by the remaining variables. These bounds are the region we label as $T$. Now that we’ve shown you the different ways we can define triple integrals, it’s time for us to learn how we can set up the limits of integration for triple integrals and eventually learn how to evaluate them.
How To Do Triple Integrals?
Use the iterated form of the triple integral to evaluate the function with respect to $x$, $y$, and $z$. Here are some general pointers to remember when working with triple integrals:
- Set up the three pairs of limits of integration correctly.
- Integrate the function with respect to the innermost variable – innermost to the outermost.
- When integrating the functions, only work with one variable while treating the remaining variables as constants.
- Evaluate the resulting expression at the given bounds then repeat the process until we have integrated it three times in a row.
The complexity of the process will actually depend on the given values. As expected, integrating the function, $f(x, y, z)$ over a rectangular box will be straightforward. It becomes more challenging when we have to integrate over a more complex region. In this section, we’ll show you examples to help you understand the process of triple integration.
Finding the Triple Integral Over a Rectangular Box
When working with a triple integral defined by a rectangular box, we simply use the limits based on the box’s bounds with respect to $x$, $y$, and $z$, respectively. Since we’re working with a rectangular box, $S$, we can define its limits as $[a, b] \times [c, d] \times [m, n]$.
\begin{aligned}\int \int \int_{S} f(x, y, z) \phantom{x} dV &= \int_{m}^{n} \int_{c}^{d} \int_{a}^{b} f(x, y, z) \phantom{x} dxdydz \end{aligned}
Let’s say we want to evaluate $\int \int \int_{S} 2xyz \phantom{x} dV$ over the region, $S = [1, 2] \times [0, 4] \times [1, 3]$. Set up the triple integral by using $[1, 2]$, $[0,4]$, and $[1, 3]$ as the limits of integrations for $x$, $y$, and $z$, respectively.
\begin{aligned}\int \int \int_{S} 2xyz \phantom{x} dV &= \int_{1}^{3} \int_{0}^{4} \int_{1}^{2} 2xyz \phantom{x} dxdydz \end{aligned}
In fact, we can switch the orders for $dx$, $dy$, $dz$, and the value of the triple integral should remain the same. Just make sure that we use the correct limits of integration for each variable! Now, let’s evaluate our triple integral, $S = \int_{1}^{3} \int_{0}^{4} \int_{1}^{2} 2xyz \phantom{x} dxdydz $, by integrating the function with respect to $x$ first since it’s the innermost function. Keep in mind that we’ll be treating $y$ and $z$ as constants.
\begin{aligned}\int_{1}^{3} \int_{0}^{4} \int_{1}^{2} 2xyz \phantom{x} dxdydz &= \int_{1}^{3} \int_{0}^{4} \left[\int_{1}^{2} 2xyz \phantom{x} dx \right ]dydz\\&= \int_{1}^{3} \int_{0}^{4} 2yz\left[\int_{1}^{2} x \phantom{x} dx \right ]dydz\\&= \int_{1}^{3} \int_{0}^{4} 2yz\left[\dfrac{x^2}{2}\right]_{1}^{2}dydz \\&= \int_{1}^{3} \int_{0}^{4} 2yz\left(\dfrac{2^2}{2} – \dfrac{1^2}{2}\right)dydz\\&= \int_{1}^{3} \int_{0}^{4} 3yz \phantom{x}dydz \end{aligned}
As we have expected, the resulting function is defined by $y$ and $z$ only. We continue integrating our double integral, now with respect to $y$ this time.
\begin{aligned}\int_{1}^{3} \int_{0}^{4} 3yz \phantom{x}dydz &= \int_{1}^{3} \left[\int_{0}^{4} 3yz \phantom{x}dy \right ]dz\\&= \int_{1}^{3} 3z\left[\int_{0}^{4} y \phantom{x}dy \right ]dz\\&= \int_{1}^{3} 3z\left[\dfrac{y^2}{2}\right ]_{0}^{4}dz\\&= \int_{1}^{3} 3z\left[\dfrac{4^2}{2} – \dfrac{0^2}{2} \right ] dz \\&= \int_{1}^{3} 24z \phantom{x}dz\end{aligned}
We’re now left with a single integral, so let’s continue to evaluate and simplify our expression.
\begin{aligned}\int_{1}^{3} 24z \phantom{x}dz &= 24\left[\dfrac{z^2}{2} \right ]_{1}^{3}\\&= 24 \left[\dfrac{3^2}{2} – \dfrac{1^2}{2}\right ]\\&= 96 \end{aligned}
Hence, we’ve shown you how to evaluate $\int_{1}^{3} \int_{0}^{4} \int_{1}^{2} 2xyz \phantom{x} dxdydz$ and in fact, it is equal to $96$. Let’s now explore a more complex example – evaluating triple integrals over a more complex region.
Finding the Triple Integral Over a General Region
When working with triple integrals that involve more complex regions, it is important that we account for the projection the region forms with respect to the $xy$, $xz$, or $yz$ planes- depending on what works for our problem.
Let us work on $\int \int \int_{S} z \phantom{x}dV$, where $S$ is a solid figure bounded by the following planes: $x = 0$, $y = 0$, $z = 0$, and $x + y + z = 4$. It is most helpful to sketch two graphs: 1) the actual solid region of $S$ and 2) the projection of $S$ on the plane (for our case, we’ll use the $xy$-plane).
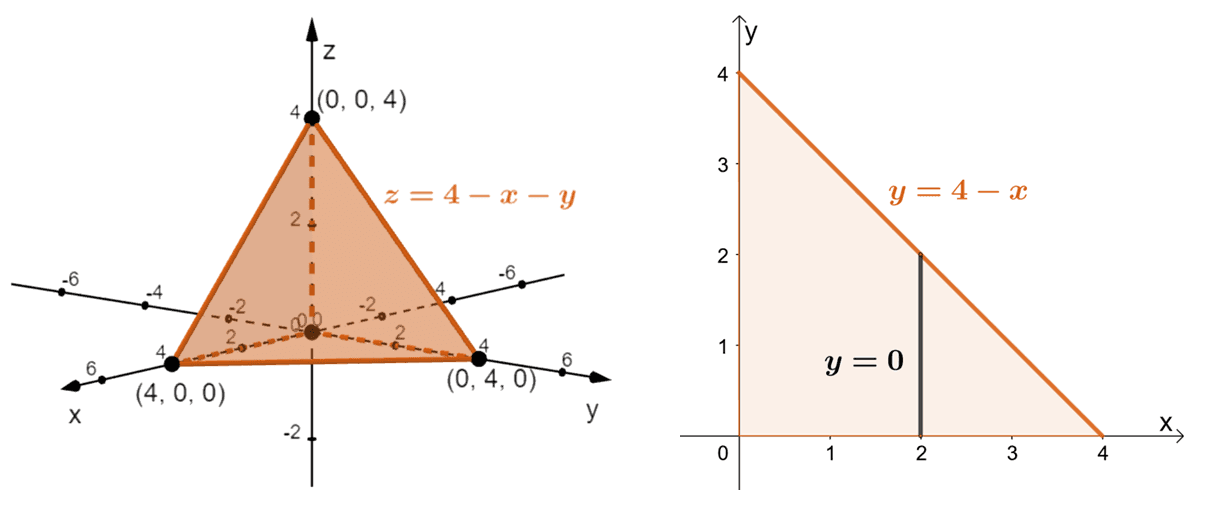
Now, the left graph represents the tetrahedron defining the volume that we’re integrating $z$ over. From the graph, we can see that with respect to $x$, our bounds are from $z = 0$ to $ z = 4- x –y$. Now, the right graph shows the projection of $S$ over the $xy$-plane. This occurs when $z = 0$, hence, we have plane bounded by $y =0$ to $y = 4 – x$ as well as $x = 0$ to $x = 4$. We can summarize the limits of integration using the notation shown below.
\begin{aligned}S &= \{(x, y, z) | 0 \leq x \leq 4, 0 \leq y \leq 4 – x, 0 \leq z \leq 4 – x –y \} \end{aligned}
Use these limits of integration to set up the complete expression for $\int \int \int_{S} z \phantom{x}dV$ – arrange the expressions so that we use the correct limits of integration for $dx$, $dy$, and $dz$.
\begin{aligned}\int \int \int_{S} z \phantom{x}dV &= \int_{0}^{4} \int_{0}^{4 – x} \int_{0}^{4 – x – y} z \phantom{x}dzdydx\end{aligned}
Once we’ve set up the triple integral, it’s time for us to evaluate the triple integral by integrating $z$ with respect to $z$ first.
\begin{aligned} \int_{0}^{4} \int_{0}^{4 – x} \int_{0}^{4 – x – y} z \phantom{x}dzdydx &= \int_{0}^{4} \int_{0}^{4 – x} \left[\int_{0}^{4 – x – y} z \phantom{x}dz \right ]dydx\\ &= \int_{0}^{4} \int_{0}^{4 – x} \left[\dfrac{z^2}{2}\right ]_{0}^{4 – x – y} dydx\\&= \dfrac{1}{2}\int_{0}^{4} \int_{0}^{4 – x} (4 – x -y)^2dydx\end{aligned}
Integrate the resulting expression with respect to $y$ then do the same with respect to $x$. We’ve simplified the calculations for you but you can work them out by applying the u-substitution method twice in a row.
\begin{aligned}\dfrac{1}{2}\int_{0}^{4} \int_{0}^{4 – x} (4 – x -y)^2dydx &= \dfrac{1}{2}\int_{0}^{4} \left[\int_{0}^{4 – x} (4 – x -y)^2dy \right ]dx\\&= \dfrac{1}{2} \int_{0}^{4} \left[- \dfrac{(4 – x – y)^3}{3}\right ]_{0}^{4 – x} dx\\&= -\dfrac{1}{6} \int_{0}^{4} [(4 – x – (4 – x))^3 – (4 – x – 0)^3]dx\\&= \dfrac{1}{6} \int_{0}^{4} (4 – x)^3 \phantom{x}dx\\&= \dfrac{1}{6}\left[-\dfrac{(4 -x)^4}{4} \right ]_{0}^{4}\\&= -\dfrac{1}{24}[(4 – 4)^4 – (4 – 0)^4]\\&= \dfrac{32}{3}\end{aligned}
From this, we can see that $\int_{0}^{4} \int_{0}^{4 – x} \int_{0}^{4 – x – y} z \phantom{x}dzdydx$ is equal to $\dfrac{32}{3}$ or approximately equal to $10.67$.
Are you getting the hang of it? Don’t worry, we’ve prepared more examples for you – from triple integrals involving rectangular boxes to integrals involving complex regions. When you’re ready to work on more problems, head over to the next section to master the process of evaluating triple integrals!
Example 1
Calculate the triple integral, $\int_{0}^{1} \int_{0}^{2} \int_{0}^{4} (xz + y) \phantom{x}dxdydz$.
Solution
The triple integral has constants as limits of integrations, so we know that we’re integrating it over a rectangular box. There is no need for us to sketch the region, so we’ll go ahead and integrate the expression three times in a row with respect to $x \rightarrow y \rightarrow z$- in that particular direction.
\begin{aligned}\int_{0}^{1} \int_{0}^{2} \int_{0}^{4} (xz + y) \phantom{x}dxdydz &= \int_{0}^{1} \int_{0}^{2} \left[\int_{0}^{4} (xz + y) \phantom{x}dx \right ]dydz\\&=\int_{0}^{1} \int_{0}^{2} \left[\dfrac{zx^2}{2} + yx\right ]_{0}^{4}dydz\\&=\int_{0}^{1} \int_{0}^{2} \left[\dfrac{z(4^2)}{2} + y(4)\right ] dydz \\&= \int_{0}^{1} \int_{0}^{2} (8z + 4y) \phantom{x}dydz\\&= \int_{0}^{1} \left[8zy + \dfrac{4y^2}{2}\right]_{0}^{2} dz\\&=\int_{0}^{1} (16z + 8) \phantom{x}dz\\&= \left[\dfrac{16z^2}{2} + 8z \right ]_{0}^{1}\\&= 8 + 8 – 0 \\&= 16 \end{aligned}
From this, we can see that $\int_{0}^{1} \int_{0}^{2} \int_{0}^{4} (xz + y) \phantom{x}dxdydz$ is equal to $16$. Apply a similar process when evaluating triple integrals over a rectangular box of any dimensions.
Example 2
Calculate the triple integral, $\int_{0}^{1} \int_{0}^{z^2} \int_{0}^{2} y\sin(z^5) \phantom{x}dxdydz$.
Solution
We’ll apply a similar process when integrating the expression, $\int_{0}^{1} \int_{0}^{z^2} \int_{0}^{2} y\sin(z^4) \phantom{x}dxdydz$. First, let’s integrate the expression with respect to $x$ first and treating the rest of the variables constant.
\begin{aligned}\int_{0}^{1} \int_{0}^{z^2} \int_{0}^{2} y\sin(z^5) \phantom{x}dxdydz &= \int_{0}^{1} \int_{0}^{z^2} \left[\int_{0}^{2} y\sin(z^5) \phantom{x}dx \right ]dydz\\&= \int_{0}^{1} \int_{0}^{z^2} \left[ y\sin(z^5)\int_{0}^{2} \phantom{x}dx \right ]dydz\\&= \int_{0}^{1} \int_{0}^{z^2} \left[ y\sin(z^5)(2 – 0) \right ]dydz\\&= \int_{0}^{1} \int_{0}^{z^2} \left[ 2y\sin(z^5)\right ]dydz\end{aligned}
Now that we have a double integral, we apply a similar process but this time, we integrate with respect to $y$ then with respect to $z$. Apply the $u$-substitution method to integrate the single integral expression. When you let $u = z^5$, we have $du = 5z^4 \phantom{x}dz$.
\begin{aligned}u &= z^5 \\ du &= 5z^4 \phantom{x}dz\\\\ \int z^4 \sin(z^5) \phantom{x}dz &= \dfrac{1}{5}\int \sin u \phantom{x}du\\&= -\dfrac{1}{5} \cos u\\&= -\dfrac{1}{5}\cos z^5\end{aligned}
Use this expression to simplify our triple integral further and find its actual value.
\begin{aligned}\int_{0}^{1} \int_{0}^{z^2} \int_{0}^{2} y\sin(z^5) \phantom{x}dxdydz &= \int_{0}^{1}z^4 \sin(z^5) \phantom{x}dz\\ &= – \dfrac{1}{5} \left[\cos z^5 \right ]_{0}^{1}\\&= -\dfrac{1}{5}[\cos 1 – 1]\\&\approx 0.0919\end{aligned}
This means that the triple integral’s value is approximately equal to $0.0919$.
Example 3
Evaluate the triple integral, $\int \int \int_{S} \sqrt{x^2 + z^2} \phantom{x}dV$, where $S$ is a solid figure bounded by the following:
\begin{aligned}\textbf{paraboloid}&: y = x^2 + z^2\\\textbf{plane}&: y = 9\end{aligned}
Solution
We’ve discussed projecting solids on the $xy$-plane and if we apply this technique to this problem, we’ll end up with a complex triple integral shown below.
\begin{aligned}\int \int \int_{S} \sqrt{x^2 + z^2} \phantom{x}dV &= \int_{-3}^{3} \int_{9}^{x^2} \int_{\sqrt{y – x^2}}^{-\sqrt{y – x^2}} sqrt{x^2 + z^2} \phantom{x}dzdydx \end{aligned}
This example will highlight why it’s helpful to also consider the other projections. Since we’re given a paraboloid, $y = x^2 + z^2$, it’s much easier to project on the $xz$-plane.
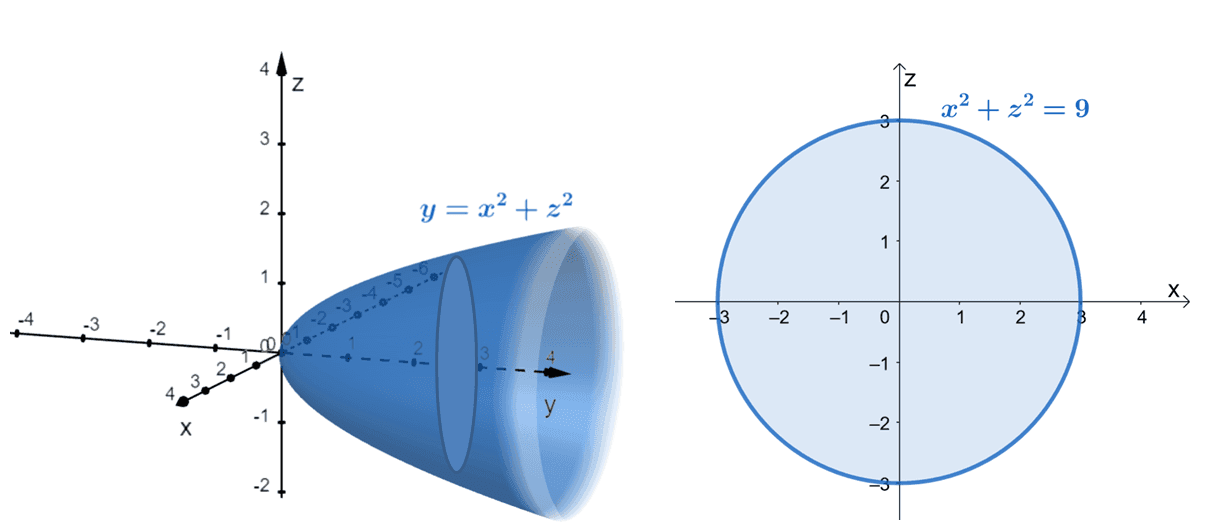
As with our previous example, it helps if you sketch the two graphs: the actual 3D figure (paraboloid) and the projected plane (circle). From the graph, we can see that the projected plane, $x^2 + z^2 = 9$, occurs only when $y = x^2 +z^2 \leq 9$. Now looking at the range of $y$ from the 3D-coordinate system, we can see that our bounds are from the paraboloid, $y = x^2 + z^2$, and the plane, $y = 9$. This means that it’s most helpful when $dy$ is the innermost differential.
\begin{aligned}\int \int \int_{S} \sqrt{x^2 + z^2} \phantom{x}dV &=\int \int_{S_{3}} \left[\int_{ x^2 + z^2}^{9 } \sqrt{x^2 + z^2} \phantom{x}dy\right] dA \end{aligned}
We won’t be expanding the rest of the triple integral, for now, so we’ll go ahead and work on integrating $\sqrt{x^2 + z^2}$ with respect to $y$.
\begin{aligned}\int_{x^2 + z^2}^{9} \sqrt{x^2 + z^2} \phantom{x}dy&=\sqrt{x^2 + z^2} \int_{x^2 + z^2}^{9} \phantom{x}dy \\&= \sqrt{x^2 + z^2} \left[y \right ]_{x^2 + z^2}^{9}\\&= \sqrt{x^2 + z^2} \left[ 9 -(x^2 + z^2)\right ]\\&= \sqrt{x^2 + z^2}(9 – x^2 -z^2) \\\\\int \int_{S_{3}} \left[\int_{9}^{x^2 + z^2} \sqrt{x^2 + z^2} \phantom{x}dy\right] dA&= \int \int_{S_3} (9 – x^2 – z^2)\sqrt{x^2 + z^2} \phantom{x}dA \end{aligned}
The reason why we’re not expanding $dA$ (although it’s possible) is that it’s much easier to evaluate the remaining double integral using polar coordinates. Using the projection on the $xz$-plane, we can rewrite $x$ as $r\cos \theta$ and $z$ as $r\sin \theta$, where $2\pi \leq \theta \leq 0$ and $0 \leq r \leq 3$. Rewrite the function and $dA$ in polar form first.
\begin{aligned}\int \int \int_{S} \sqrt{x^2 + z^2} \phantom{x}dV &= \int \int_{S_3} (9 – x^2 – z^2)\sqrt{x^2 + z^2} \phantom{x}dA \\&= \int_{0}^{2\pi} \int_{0}^{3} (9 – r^2) \sqrt{r^2} \phantom{x}rdrd\theta\\&= \int_{0}^{2\pi} \int_{0}^{3} (9r^2 – r^4) \phantom{x}drd\theta\end{aligned}
Evaluate the resulting double integral in polar coordinates. Integrate the expression with respect to $r$ then with respect to $\theta$. Check out our calculations below in case you need a guide in working out the double integral.
\begin{aligned}\int \int \int_{S} \sqrt{x^2 + z^2} \phantom{x}dV &= \int_{0}^{2\pi} \int_{0}^{3} (9r^2 – r^4) \phantom{x}drd\theta\\&=\int_{0}^{2\pi} \left[ \int_{0}^{3} (9r^2 – r^4) \phantom{x}dr\right ]d\theta \\&= \int_{0}^{2\pi} \left[3r^3 – \dfrac{r^5}{5} \right ]_{0}^{3} \phantom{x}d\theta\\&= \int_{0}^{2\pi} \dfrac{162}{5} \phantom{x}d\theta\\&= \dfrac{162}{5} (2\pi)\\&= \dfrac{324\pi}{5}\end{aligned}
This means that $\int \int \int_{S} \sqrt{x^2 + z^2} \phantom{x}dV$ is equal to $\dfrac{324\pi}{5}$ or approximately equal to $203.58$. You can also try setting up the triple integral in Cartesian form and confirm that they return the same value!
Example 4
One of the important applications of triple integrals is finding a solid object’s mass, moments, and center of mass. We can represent these components using the triple integrals shown below.
| Mass | \begin{aligned}m &= \int \int \int_{S} \rho(x, y, z) \phantom{x}dV\end{aligned} |
| Moments | \begin{aligned}M_{yz} &= \int \int \int_{S} x\rho(x, y, z) \phantom{x}dV\\M_{xz} &= \int \int \int_{S} y\rho(x, y, z) \phantom{x}dV\\M_{xy} &= \int \int \int_{S} z\rho(x, y, z) \phantom{x}dV\end{aligned} |
| Center of Mass | \begin{aligned}\overline{x} &= \dfrac{M_{yz}}{m} \\\overline{y} &= \dfrac{M_{xz}}{m}\\ \overline{z} &= \dfrac{M_{xy}}{m} \end{aligned} |
Determine the center of mass of a solid with a constant density, $\rho(x, y, z)$, bounded by the solid, $x = 4y^2$, and the following planes: $x = 2z$, $z = 0$, and $x = 4$.
Solution
First, let’s visualize how the solid (it’s in fact a parabolic cylinder) looks like and its project on the $xy$-plane.
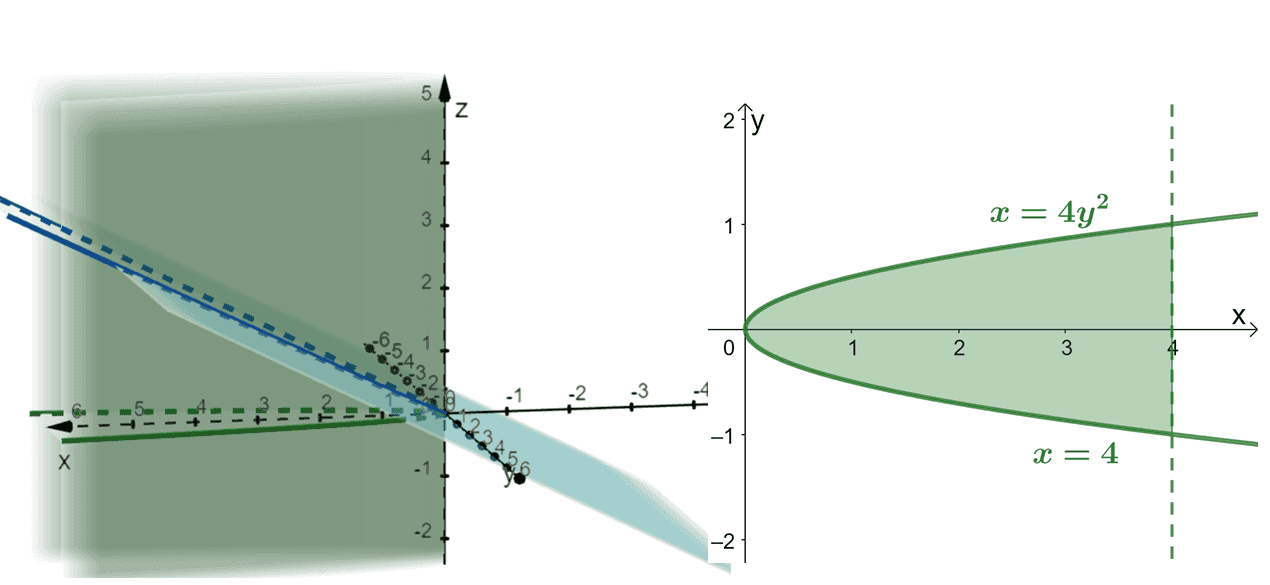
The graphs above highlight the solid, $S$, and its projection on the $xy$-plane. Using these regions, we can set up the bounds of $S$ as shown below.
\begin{aligned}S&= \left\{(x, y, z) | -1 \leq y \leq 1, 4y^2 \leq x \leq 4, 0 \leq z\leq \dfrac{x}{2}\right\}\end{aligned}
We can set up the triple integral representing the mass of the solid first and let $\rho (x, y,z)$ as the constant, $\rho$.
\begin{aligned}m &= \int \int\int_{S} \rho\phantom{x}dV\\&= \int_{-1}^{1}\int_{4y^2}^{4}\int_{0}^{x/2} \rho \phantom{x}dzdxdy\end{aligned}
Evaluate the expression by integrating the function with respect to the following variables in this specific order: $z \rightarrow x \rightarrow y$.
\begin{aligned}\int_{-1}^{1}\int_{4y^2}^{4}\int_{0}^{x/2} \rho \phantom{x}dzdxdy &= \int_{-1}^{1}\int_{4y^2}^{4}\left[\int_{0}^{x/2} \rho \phantom{x}dz \right ]dxdy\\&= \rho\int_{-1}^{1}\int_{4y^2}^{4}\dfrac{x}{2} \phantom{x} dxdy\\&= \dfrac{\rho}{2}\int_{-1}^{1}\left[\dfrac{x^2}{2}\right]_{4y^2}^{4}\phantom{x}dy\\&=\dfrac{\rho}{4}\int_{-1}^{1} (16 – 16y^4)\phantom{x}dy\\&= 4\rho\int_{-1}^{1} (1- y^4)\phantom{x} dy\\&= \dfrac{32\rho}{5}\end{aligned}
In terms of the constant density, $\rho$, the mass of the solid object is equal to $\dfrac{32 \rho}{5}$. Now that we have the mass of the object, it’s time for us to calculate its moments as shown below.
| \begin{aligned}\boldsymbol{M_{yz} = \int \int \int_{S} x\rho(x, y, z)dV}\end{aligned} | \begin{aligned}\int_{-1}^{1}\int_{4y^2}^{4}\int_{0}^{x/2} x\rho \phantom{x}dzdxdy &= \int_{-1}^{1}\int_{4y^2}^{4}\left[\int_{0}^{x/2} x\rho \phantom{x}dz \right ]dxdy \\&= \rho \int_{-1}^{1}\int_{4y^2}^{4} \dfrac{x^2}{2} \phantom{x}dxdy \\&= \dfrac{\rho}{2} \int_{-1}^{1}\left[\dfrac{x^3}{3}\right]_{4y^2}^{4} \phantom{x}dy \\&=\dfrac{\rho}{6} \int_{-1}^{1}\left[4^3 – (4y^2)^3\right] \phantom{x}dy \\&= 64\cdot\dfrac{\rho}{6} \int_{-1}^{1} (1 – y^6) \phantom{x}dy\\&= \dfrac{32\rho}{3}\left[y – \dfrac{y^7}{7} \right ]_{-1}^{1}\\&= \dfrac{128\rho}{7} \end{aligned} |
| \begin{aligned}\boldsymbol{M_{xz} = \int \int \int_{S} y\rho(x, y, z)dV}\end{aligned} | \begin{aligned}\int_{-1}^{1}\int_{4y^2}^{4}\int_{0}^{x/2} y\rho \phantom{x}dzdxdy &= \int_{-1}^{1}\int_{4y^2}^{4}\left[\int_{0}^{x/2} y\rho \phantom{x}dz \right ]dxdy \\&= \rho \int_{-1}^{1}\int_{4y^2}^{4} \dfrac{yx}{2} \phantom{x}dxdy \\&= \dfrac{\rho}{2} \int_{-1}^{1}\left[\dfrac{yx^2}{2}\right]_{4y^2}^{4} \phantom{x}dy \\&=\dfrac{\rho}{4} \int_{-1}^{1}\left[4^2y – (4y^2)^2y\right] \phantom{x}dy \\&= 4\rho\int_{-1}^{1} (y – y^3) \phantom{x}dy\\&= 4\rho\left[\dfrac{y^2}{2} – \dfrac{y^4}{4} \right ]_{-1}^{1}\\&= 0\end{aligned} |
| \begin{aligned}\boldsymbol{M_{xy} = \int \int \int_{S} z\rho(x, y, z)dV}\end{aligned} | \begin{aligned}\int_{-1}^{1}\int_{4y^2}^{4}\int_{0}^{x/2} z\rho \phantom{x}dzdxdy &= \int_{-1}^{1}\int_{4y^2}^{4}\left[\int_{0}^{x/2} z\rho \phantom{x}dz \right ]dxdy \\&= \rho \int_{-1}^{1}\int_{4y^2}^{4} \dfrac{x^2/4}{2} \phantom{x}dxdy \\&= \dfrac{\rho}{8} \int_{-1}^{1}\left[\dfrac{x^3}{3}\right]_{4y^2}^{4} \phantom{x}dy \\&=\dfrac{\rho}{24} \int_{-1}^{1}\left[4^3 – (4y^2)^3\right] \phantom{x}dy \\&= 64\cdot\dfrac{\rho}{24} \int_{-1}^{1} (1 – y^6) \phantom{x}dy\\&= \dfrac{8\rho}{3}\left[y – \dfrac{y^7}{7} \right ]_{-1}^{1}\\&= \dfrac{32\rho}{7} \end{aligned} |
Now that we have the moments as well as the mass of the object, we can now find the coordinates for its center of mass using the equation, $(\overline{x}, \overline{y}, \overline{z}) = \left(\dfrac{M_{yz}}{m}, \dfrac{M_{xz}}{m}, \dfrac{M_{xy}}{m}\right)$.
| \begin{aligned} \boldsymbol{\overline{x}}\end{aligned} | \begin{aligned} \boldsymbol{\overline{y}}\end{aligned} | \begin{aligned} \boldsymbol{\overline{z}}\end{aligned} |
| \begin{aligned}\overline{x}&= \dfrac{M_{yz}}{m}\\&= \dfrac{\dfrac{128\rho}{7}}{\dfrac{32\rho}{5}}\\&= \dfrac{20}{7}\end{aligned} | \begin{aligned}\overline{x}&= \dfrac{M_{xz}}{m}\\&= \dfrac{0}{\dfrac{32\rho}{5}}\\&= 0\end{aligned} | \begin{aligned}\overline{z}&= \dfrac{M_{xy}}{m}\\&= \dfrac{\dfrac{32\rho}{7}}{\dfrac{32\rho}{5}}\\&= \dfrac{5}{7}\end{aligned} |
| \begin{aligned}\boldsymbol{(\overline{x}, \overline{y}, \overline{z})} &= \left(\dfrac{20}{7}, 0, \dfrac{5}{7}\right) \end{aligned} | ||
This means that the solid has a center of mass at $\left(\dfrac{20}{7}, 0, \dfrac{5}{7}\right)$. This problem shows just one of the many applications of triple integrals. This is why it’s important that we understand how to set up and evaluate triple integrals. When you’re ready, we’ve prepared more examples for you to try!
Practice Questions
1. Calculate the triple integral, $\int_{0}^{2} \int_{0}^{4} \int_{0}^{1} (xy -z) \phantom{x}dxdydz$.
2. Calculate the triple integral, $\int_{0}^{2} \int_{0}^{z^2} \int_{0}^{3} y\cos(z^5) \phantom{x}dxdydz$.
3. Evaluate the triple integral, $\int \int \int_{S} z \phantom{x}dV$, where $S$ is a solid figure bounded by the following planes: $x = 0$, $y = 0$, $z = 0$, and $x + y + z = 9$.
4. Evaluate the triple integral, $\int \int \int_{S} \sqrt{x^2 + z^2} \phantom{x}dV$, where $S$ is a solid figure bounded by the following:
\begin{aligned}\textbf{paraboloid}&: y = x^2 + z^2\\\textbf{plane}&: y = 16\end{aligned}
5. Set up a triple integral to determine the volume of the tetrahedron, $S$, bounded by the following planes: $x = 0$, $x = 4y$, $z = 0$, and $x + 4y + z = 4$.
6. Determine the center of mass of a solid with a constant density, $\rho(x, y, z)$, bounded by the solid, $x = y^2$, and the following planes: $x = z$, $z = 0$, and $x = 1$.
Answer Key
1. $\int_{0}^{9} \int_{0}^{9 – x} \int_{0}^{9 – x – y} z \phantom{x}dzdydx = \dfrac{2187}{8}$
2. $\int_{0}^{2} \int_{0}^{z^2} \int_{0}^{3} y\cos(z^5) \phantom{x}dxdydz = \dfrac{3\sin 32}{10} \approx 0.165$
3. $\int_{0}^{2} \int_{0}^{4} \int_{0}^{1} (xy -z) \phantom{x}dxdydz = 0$
4.$\int \int_{S_3} \left[\int_{x^2 + z^2}^{16} \sqrt{x^2 + z^2}\phantom{x} dy\right] dA = \dfrac{4096\pi}{15} \approx 857.86$
5. $\int_{0}^{2} \int_{x/4}^{1- x/4} \int_{0}^{4 – x – 4y} \phantom{x}dzdydx = \dfrac{4}{3}$
6. $(\overline{x}, \overline{y}, \overline{z}) = \left(\dfrac{5}{7}, 0, \dfrac{5}{14}\right)$
Images/mathematical drawings are created with GeoGebra.
