- Home
- >
- Zeros of a function – Explanation and Examples
JUMP TO TOPIC
Zeros of a function – Explanation and Examples
 One of the most common problems we’ll encounter in our basic and advanced Algebra classes is finding the zeros of certain functions – the complexity will vary as we progress and master the craft of solving for zeros of functions.
One of the most common problems we’ll encounter in our basic and advanced Algebra classes is finding the zeros of certain functions – the complexity will vary as we progress and master the craft of solving for zeros of functions.
From its name, the zeros of a function are the values of x where f(x) is equal to zero.
We find zeros in our math classes and our daily lives. For example, if we want to know the amount we need to sell to break even, we’ll end up finding the zeros of the equation we’ve set up. That’s just one of the many examples of problems and models where we need to find f(x) zeros.
With the extensive application of functions and their zeros, we must learn how to manipulate different expressions and equations to find their zeros. In this article, we’ll learn to:
- Know what a function’s zero represents.
- Learn how to find the zeros of common functions.
- Identify zeros of a function from its graph.
Let’s go ahead and start with understanding the fundamental definition of a zero.
What is the zero of a function?
Understanding what zeros represent can help us know when to find the zeros of functions given their expressions and learn how to find them given a function’s graph. In general, a function’s zeros are the value of x when the function itself becomes zero.
The zeros of a function may come in different forms – as long as they return a y-value of 0, we will count it as the function’s zero.
Zeros of a function definition
The zeros of a function are the values of x when f(x) is equal to 0. Hence, its name. This means that when f(x) = 0, x is a zero of the function. When the graph passes through x = a, a is said to be a zero of the function. Hence, (a, 0) is a zero of a function.
- The function f(x) = x + 3 has a zero at x = -3 since f(-3) = 0.
- The function g(x) = x2 – 4 has two zeros: x = -4 and x = 4. This means that f(-4) = 0 and f(4) = 0.
- The graph of h(x) passes through (-5, 0), so x = -5 is a zero of h(x) and h(-5) = 0.
When given the graph of a function, its real zeros will be represented by the x-intercepts. This makes sense since zeros are the values of x when y or f(x) is 0.
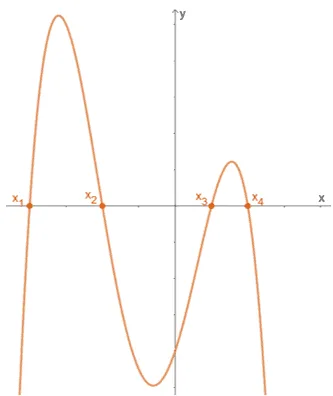
The x-intercepts of the function are (x1, 0), (x2, 0), (x3, 0), and (x4, 0). This means that for the graph shown above, its real zeros are {x1, x2, x3, x4}.
There are instances, however, that the graph doesn’t pass through the x-intercept. This doesn’t mean that the function doesn’t have any zeros, but instead, the functions’ zeros may be of complex form.
How to find the zeros of a function?
Finding the zeros of a function can be as straightforward as isolating x on one side of the equation to repeatedly manipulating the expression to find all the zeros of an equation.
In general, given the function, f(x), its zeros can be found by setting the function to zero. The values of x that represent the set equation are the zeroes of the function. To find the zeros of a function, find the values of x where f(x) = 0.
How to find zeros of a quadratic function?
There are a lot of complex equations that can eventually be reduced to quadratic equations. This is why in our intermediate Algebra classes, we’ll spend a lot of time learning about the zeros of quadratic functions.
To find the zeros of a quadratic function, we equate the given function to 0 and solve for the values of x that satisfy the equation. Here are some important reminders when finding the zeros of a quadratic function:
- Make sure the quadratic equation is in standard form (ax2 + bx + c = 0).
- Factor whenever possible, but don’t hesitate to use the quadratic formula.
- A quadratic function can have at most two zeros.
We’ve learned about the different strategies for finding the zeros of quadratic functions in the past, so here’s a guide on how to choose the best strategy:
| Guide Questions | Strategy |
| Is the quadratic function factorable? | Use factoring techniques to solve the quadratic equation. |
| Does the quadratic function exhibit special algebraic properties? | Solve the equation using the difference of two square or perfect square trinomial. |
| Is the function not factorable? | Apply the quadratic formula. |
How to find zeros of a polynomial function?
The same process applies for polynomial functions – equate the polynomial function to 0 and find the values of x that satisfy the equation. This guide can help you in finding the best strategy when finding the zeros of polynomial functions.
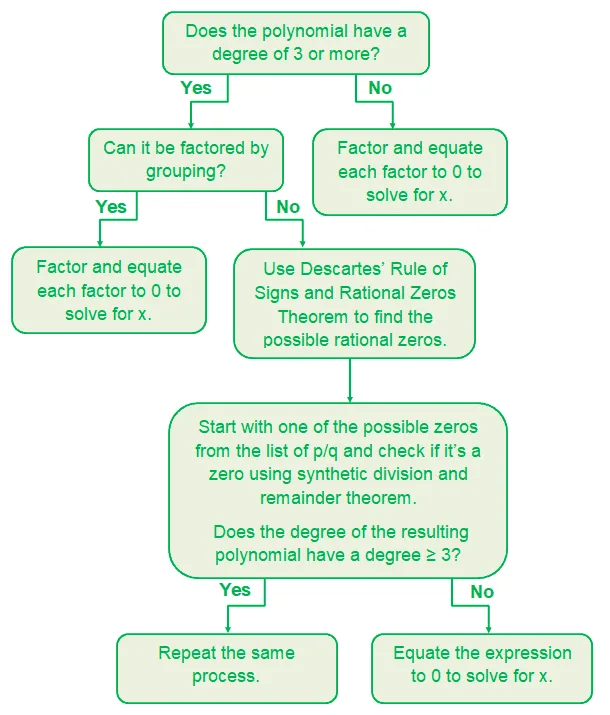
Need further review on solving polynomial equations? No worries, check out this link here and refresh your knowledge on solving polynomial equations.
How to find zeros of a rational function?
Rational functions are functions that have a polynomial expression on both their numerator and denominator. Applying the same principle when finding other functions’ zeros, we equation a rational function to 0.
Let’s say we have a rational function, f(x), with a numerator of p(x) and a denominator of q(x).
f(x) = p(x)/q(x)
To find its zero, we equate the rational expression to zero.
p(x)/q(x) = 0
Since q(x) can never be equal to zero, we simplify the equation to p(x) = 0. What does this mean for all rational functions?
When finding the zero of rational functions, we equate the numerator to 0 and solve for x.
How to find zeros of other functions?
As you may have guessed, the rule remains the same for all kinds of functions. When given a unique function, make sure to equate its expression to 0 to finds its zeros.
Here are some more functions that you may already have encountered in the past:
| Type of Function | Example |
| Logarithmic Function | f(x) = log2 2x Learn how to solve logarithmic equations here. |
| Power Function | f(x) = 3x1/3 Practice solving equations involving power functions here. |
| Exponential Function | f(x) = 2x + 1 |
| Trigonometric Function | f(x) = -3 sin x |
The zeros from any of these functions will return the values of x where the function is zero. When given the graph of these functions, we can find their real zeros by inspecting the graph’s x-intercepts.
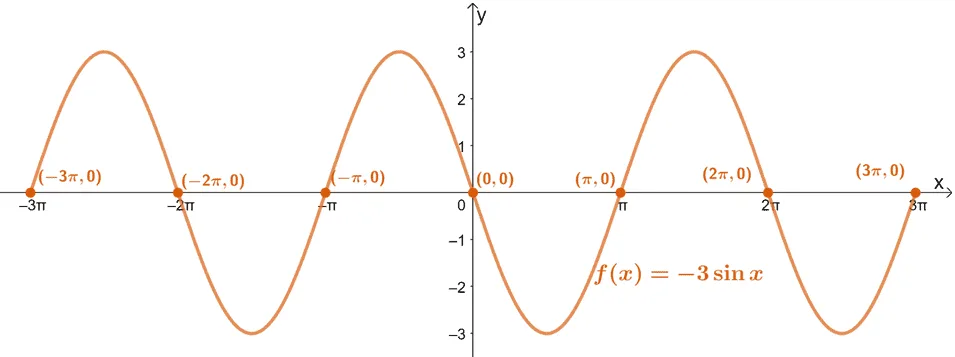
The graph above is that of f(x) = -3 sin x from -3π to 3π. All the x-intercepts of the graph are all zeros of function between the intervals. Hence, the zeros between the given intervals are: {-3π, -2π, – π, 0, π, 2π, 3π}.
Ready to apply what we’ve just learned? Let’s go ahead and try out some of these problems.
Example 1
The function f(x) has the following table of values as shown below.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | 64 | 9 | 0 | 1 | 0 | 9 | 64 |
Based on the table, what are the zeros of f(x)?
Solution
Always go back to the fact that the zeros of functions are the values of x when the function’s value is zero.
We can see that when x = -1, y = 0 and when x = 1, y = 0 as well. Hence, the zeros of f(x) are -1 and 1.
Example 2
The graph of f(x) is shown below. Using this graph, what are the zeros of f(x)?
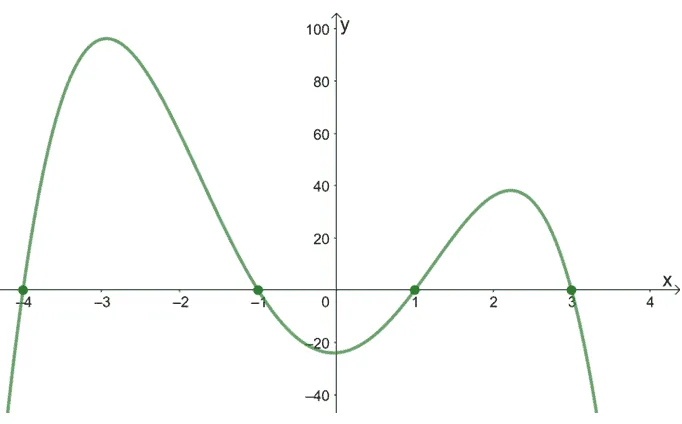
Solution
The graph of f(x) passes through the x-axis at (-4, 0), (-1, 0), (1, 0), and (3, 0). These are the x-intercepts and consequently, these are the real zeros of f(x).
Hence, the zeros of f(x) are {-4, -1, 1, 3}.
Example 3
What are the zeros of g(x) = –x3 – 3x2 + x + 3?
Solution
Find the zero of g(x) by equating the cubic expression to 0.
–x3 – 3x2 + x + 3 = 0
Rearrange the equation so we can group and factor the expression.
–x3 + x – 3x2 + 3 = 0
-x(x2 – 1) – 3(x2 – 1) = 0
(-x-3)(x2 – 1) = 0
Apply the difference of two squares property, a2 – b2 = (a – b),(a + b) on the second factor.
(-x-3)(x – 1)(x + 1) = 0
Equate each factor to 0 to find for x.
-x- 3 = 0 -x = 3 x = 3 | x – 1 = 0 x = 1 | x + 1 = 0 x = -1 |
Hence, the zeros of g(x) are {-1, 1, 3}.
Example 4
What are the zeros of h(x) = –2x4 – 2x3 + 14x2 + 2x – 12?
Solution
Equate the expression of h(x) to 0 to find its zeros. This will result in a polynomial equation.
–2x4 – 2x3 + 14x2 + 2x – 12 = 0
Divide both sides of the equation to -2 to simplify the equation.
x4 + x3 – 7x2 – x + 6 = 0
List down the possible rational factors of the expression using the rational zeros theorem. For our case, we have p = 1 and q = 6.
| Factors of p | ±1 |
| Factors of q | ±1, ±2, ±3, ±6 |
| Possible zeros (p/q) | ±1/6, ±1/3, ±1/2, ±1 |
Let’s go ahead and use synthetic division to see if x = 1 and x = -1 can satisfy the equation.
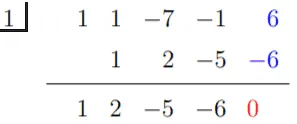
This means that x = 1 is a solution and h(x) can be rewritten as -2(x – 1)(x3 + 2x2 -5x – 6). Use the cubic expression in the next synthetic division and see if x = -1 is also a solution.
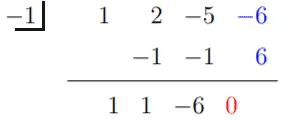
Hence, x = -1 is a solution and (x + 1) is a factor of h(x). Hence, we have h(x) = -2(x – 1)(x + 1)(x2 + x – 6).
To find the two remaining zeros of h(x), equate the quadratic expression to 0.
x2 + x – 6 = 0
(x – 3)(x + 2) = 0
x + 2 = 0 x = -2 | x – 3 = 0 x = 3 |
Hence, the zeros of h(x) are {-2, -1, 1, 3}.
Example 5
What are the zeros of g(x) = (x4 -10x2 + 9)/(x2 – 4)?
Solution
The function g(x) is a rational function, so to find its zero, equate the numerator to 0.
x4 -10x2 + 9 = 0
Solve for x that satisfies the equation to find the zeros of g(x).
Let a = x2 and reduce the equation to a quadratic equation.
(x2)2 – 10x2 + 9 = 0
a2 – 10a + 9 = 0
(a – 1)(a – 9) = 0
Equate each factor to 0 to find a then substitute x2 back to find the possible values of g(x)’s zeros.
a – 1 =0 x2 – 1 = 0 x2 = 1 x = ± 1 | a – 9 =0 x2 – 9 = 0 x2 = 9 x = ± 3 |
Hence, the zeros of g(x) are {-3, -1, 1, 3}.
Practice Questions
![]()
Images/mathematical drawings are created with GeoGebra.
