Alternating series test – Definition, Conditions, and Examples

The alternating series test is one of the common convergence tests you’ll learn in your precalculus and calculus class. It’s also one of the easiest tests to apply, so it’ll come in handy when we’re left with a few choices in testing the convergence of a particular series.

The alternating series test (or also know as the Leibniz test) helps us determine whether a given alternating series is convergent or not.

In this article, we’ll learn what type of series will benefit from the alternating series test. We’ll also review how we can confirm whether the series is alternating and apply important limit laws.
This means that it’s important to prepare before diving right into the main topic:
• Review what makes alternating series special and how we can confirm if the terms of the series are increasing or not.
• Make sure to review your knowledge on limit laws and properties that need to evaluate limits.

Let’s begin by visualizing how an alternating series behaves and what to expect from the partial sum of the series as $n$ approaches infinity.

What is the alternating series test?                

The alternating series test is utilized to test a given alternating series’ convergence or divergence.

It’s a test that uses the nature of $a_n$ as well as the behavior of the nth term as it approaches infinity.

Recall that the alternating series is a special type of series where the signs of the terms are alternating.

Review what makes alternating series special and how we can confirm if the terms of the series are increasing or not.

Make sure to review your knowledge on limit laws and properties that need to evaluate limits.

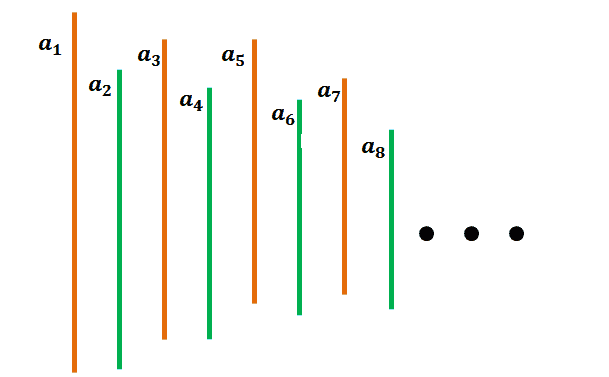
The image above is a good visualization of how an alternating series behaves as we expand the terms.

To predict the value of the sum (chances are it’s somewhere in the middle), it helps to know how the new terms behave as $n$ approaches infinity.

Before we do so, it will save us time to know whether the sum of the series approaches a certain value. It helps if we also know if the sum alternates to a particular value or not.

To confirm the convergence of a particular series, the alternating series test plays a huge role. We’ll learn more about the process and conditions of this particular test in the next sections.

Alternating series test definition

The alternating series test (or also known as the Leibniz test) is an essential infinite series test used in predicting whether a given alternating series is convergent or not.

\begin{aligned} \lim_{n \rightarrow \infty} (-1)^n a_n = S\end{aligned}

The alternating series test can confirm whether the alternating series converges to a sum, $S$, as $n$ approaches infinity.

According to the alternating series test, if the alternating series’s terms continue to decrease and approach $0$, the series is convergent.

In the next section, we’ll dive right into the actual process of the alternating series test.

How to do alternating series test?                

Let’s say we have an infinite series,$\sum_{n=1}^{\infty} a_n$, to check if it is convergent using the alternating series test, we can follow the steps shown below:

Step 1: Check if the series is an alternating series – they are normally of the forms, $\sum_{n=1}^{\infty} (-1)^n a_n$ or $\sum_{n=1}^{\infty} (-1)^{n + 1} a_n$ .

Step 2: Make sure that the series meets the conditions required by the alternating series test.

Step 3: If the alternating series meets the two conditions, the series is convergent.

Alternating series test conditions

We’ve mentioned the conditions we need for the alternating series to meet before applying the alternating series test. Given that $a_n > 0$ for all values of $n$, below are the two important conditions you’ll need to meet:

1. The value of $a_n$ is a decreasing sequence for large values of $n$ (or as it approaches infinity).

2. The value of $\lim_{n \rightarrow \infty}$ is equal to $0$.

When these conditions are met, we can conclude that $\sum_{n=1}^{\infty} a_n$ is convergent.

Let’s say we have $-1 + \dfrac{1}{4} – \dfrac{1}{9} + \dfrac{1}{16} – ….$.

By inspection, we can see that the terms alternate in signs. Observing the first four terms, we have:

\begin{aligned}-1 &= (-1)^1 \cdot \dfrac{1}{1^2}\\ \dfrac{1}{4} &= (-1)^2 \cdot \dfrac{1}{2^2}\\-\dfrac{1}{9} &= (-1)^3 \cdot \dfrac{1}{3^2}\\\dfrac{1}{16} &= (-1)^4 \cdot \dfrac{1}{4^2}\\.\\.\\.\end{aligned}

This means that we can actually express the series above as $\sum_{n=1}^{\infty} (-1)^n \dfrac{1}{n^2}$. After confirming that the series is indeed an alternating series, we can now check the series for the two conditions:

1. We can see that as $n$ increases, the value of $\dfrac{1}{n^2}$ decreases.

2. $\lim_{n\rightarrow \infty} \dfrac{1}{n^2} = 0$

Since the series meets the two conditions, we can conclude that the given series is convergent at $0$.

This is a great example showing how it is easy for us to apply this series once we identify and confirm that the terms satisfy the required conditions. Before we try out more problems, why don’t we go ahead and understand the proof of this particular test?

Proof of Leibniz test or alternating series test

The other name for the alternating series test is called the Leibniz test. This is why this section included its name, just in case you encounter this in your higher math classes.

In this section, we’ll show you why the alternating series test or the Leibniz test works. Let’s say we have $ \sum_{n=1}^{\infty} (-1)^n a_n$ – we can observe the behavior of the partial sums as we add more terms. Particularly, let’s focus on the behavior of $S_n$ when $n$ is even.

\begin{aligned}S_2 &= a _1 – a_2 > 0 \\S_4 &= S_2 + (a_3 – a_4) \geq S_2\\S_6 &= S_4 + (a_5 – a_6) \geq S_4\\.\\.\\.\end{aligned}

This means that the value of $S_{2n}$ is expected to be larger than $S_{2n – 2}$. We can also use our observations from the first three even sums to relate the sums as shown below.

\begin{aligned} S_{2n} &= S_{2n – 2} + (a_{2n – 1} – a_{2n}) \geq S_{2n – 2} \end{aligned}

What does this mean for the series? The sum continues to grow for $S_{2n}$.

\begin{aligned}S_2n &= a_1 – a_2 + a_3 – a_4 + …-a_{2n – 2} + a_{2n – 1} – a_{2n}\\&= a_1 – (a_2 – a_3) -(a_4 – a_5) + … -(a_{2n – 2} – a_{2n – 1}) – a_{2n}\end{aligned}

By rewriting the expression the $2n$th partial sum, we can see that $s_{2n}$ is indeed less than or equal to $a_1$.

We have established that $S_{2n}$ is increasing and is bounded, so it’s given that the sequence is convergent. Let’s say $S = \lim_{n \rightarrow} S_{2n}$, we can find the limit of $S_{2n + 1}$ as shown below.

\begin{aligned}\lim_{n \rightarrow \infty} S_{2n + 1} &= \lim_{n \rightarrow \infty} (S_{2n} + a_{2n + 1})\\&= \lim_{n \rightarrow \infty} S_{2n} +\lim_{n \rightarrow \infty} a_{2n + 1}\\&= S + 0\\&= S\end{aligned}

Since the limit for $S_{2n}$ and $S_{n+1}$ as $n$ approaches infinity is equal to $S$, and $S_{2n}$ is convergent, this shows that the series is indeed convergent and a limit of $S$.

We’ve discussed everything we need to know about the alternating series test, so let’s go ahead and apply this test to confirm a certain series is convergent or not.

Example 1

Determine if the series,$ \sum_{n=1}^{\infty} \dfrac{(-1)^n }{2n + 5}$, is convergent or divergent.

Solution

We can first rewrite the series to check if it is indeed an alternating series.

\begin{aligned}\sum_{n=1}^{\infty} \dfrac{(-1)^n }{2n + 5} &= \sum_{n=1}^{\infty} (-1)^n \dfrac{1}{2n + 5}\end{aligned}

This shows that the series is indeed an alternating series. We can even write down the first few terms to confirm this.

The first four terms of the series confirm that the series contains terms that are alternating in sign. Now, let’s go ahead and check if the series satisfies the first condition of the alternating series test.

When $n > 0 $, $2n + 5$ will be smaller than $2(n + 1) + 5 = 2n + 7$.

\begin{aligned}2n + 5 &< 2n + 7\\\dfrac{1}{2n + 5} &> \dfrac{1}{2n + 7}\\a_n &> a_{n + 1}\end{aligned}

Since $a_{n + 1}$ is smaller than $a_n$, we can see that the series’ terms are decreasing as the $n$ increases. Meaning, the series satisfies the first condition.

The second condition requires us to check the value of $\lim_{n \rightarrow \infty} a_n$, where $a_n = \dfrac{1}{2n + 5}$.

\begin{aligned}\lim_{n\rightarrow \infty} \dfrac{1}{2n + 5} &= \lim_{n\rightarrow \infty} \dfrac{1}{2n + 5}\cdot \dfrac{\dfrac{1}{n}}{\dfrac{1}{n}}\\&= \lim_{n \rightarrow \infty} \dfrac{\dfrac{1}{n}}{2 + \dfrac{5}{n}}\\&= \dfrac{\lim_{n \rightarrow \infty} \dfrac{1}{n}}{\lim_{n \rightarrow \infty} 2 + \dfrac{5}{n}}\\&= \dfrac{0}{2 +0 }\\&= 0 \end{aligned}

Since we have shown that the limit of $a_n$ is equal to $0$, we can conclude that the series is convergent.

Example 2

Determine if the series,$ \sum_{n=1}^{\infty} \dfrac{(-1)^n n^2}{n^2 + 8}$, is convergent or divergent.

Solution

First, let’s rewrite the series as shown below.

\begin{aligned}\sum_{n=1}^{\infty} \dfrac{(-1)^n n^2}{n^2 + 8} &= \sum_{n=1}^{\infty} (-1)^n \dfrac{n^2}{n^2 + 8}\end{aligned}

From this, we can see that the series is an alternating series of the form, $\sum_{n=1}^{\infty} (-1)^n a_n$, where $a_n = \dfrac{n^2}{n^2 + 8}$. We can now check if the two conditions are met by the series.

\begin{aligned}n^2 &< (n + 1)^2\\n^2 + 8 &< (n + 1)^2 + 8\\\dfrac{n^2}{n^2 + 8} &>\dfrac{(n + 1)^2}{(n + 1)^2 + 8}\\a_n &> a_{n + 1}\end{aligned}

We can see that terms progress in the series, the value of $a_n$ decreases. This means the series meets the first condition required for the test. We can now take the limit of $a_n$ as $n$ approaches infinity.

\begin{aligned}\lim_{n\rightarrow \infty} \dfrac{n^2}{n^2 + 8} &=\lim_{n\rightarrow \infty} \dfrac{n^2}{n^2 + 8} \cdot \dfrac{\dfrac{1}{n^2}}{\dfrac{1}{n^2}}\\&= \lim_{n\rightarrow \infty} \dfrac{1}{1 + \dfrac{8}{n^2}}\\&= \dfrac{1}{1 +0}\\&= 1\\&\neq 0\end{aligned}

We can see that $\lim_{n \rightarrow \infty} a_n \neq 0$, so the series does not meet the conditions for it to be convergent. What do we do now? Since we can’t conclude that the series is convergent, we can then see if the series is divergent.

We can do this by finding the value of $\lim_{n\rightarrow \infty} (-1)^n \dfrac{n^2}{n^2 + 8}$.

\begin{aligned}\lim_{n\rightarrow \infty}\left[(-1)^n \dfrac{n^2}{n^2 + 8}\right]&= \left[\lim_{n\rightarrow \infty}(-1)^n \right]\left(\lim_{n\rightarrow \infty}\dfrac{n^2}{n^2 + 8} \right)\\&=\left[\lim_{n\rightarrow \infty}(-1)^n \right](1)\\&=\lim_{n\rightarrow \infty}(-1)^n\end{aligned}

From this, we can see that the limit alternates between $-1$ and $1$, so we can say that the series is indeed divergent.

Example 3

Determine if the series,$ \sum_{n=1}^{\infty} \dfrac{(-1)^n }{\sqrt{n + 1}}$, is convergent or divergent.

Solution

Why don’t we go ahead and check the first few terms of the series?

\begin{aligned} \sum_{n=1}^{\infty} \dfrac{(-1)^n }{\sqrt{n + 1}} &= \sum_{n=1}^{\infty}(-1)^n\dfrac{1}{\sqrt{n + 1}}\\\\a_1 &= -\dfrac{1}{\sqrt{2}}\\a_2 &= \dfrac{1}{\sqrt{3}}\\a_3 &= -\dfrac{1}{\sqrt{4}}\\a_4 &= \dfrac{1}{\sqrt{5}}\\.\\.\\. \end{aligned}

From this, we can see that the series is indeed an alternating series. Since we’ve confirmed the nature of the series, we can now review the two conditions that we need to check to confirm whether the series is convergent or not.

Let’s first confirm is $a_{n + 1}$ is indeed smaller than $a_n$:

\begin{aligned} n + 1 &> n\\(n + 1) + 1 &> n + 1\\n + 2 &> n + 1\\\dfrac{1}{n + 2} &\leq \dfrac{1}{n + 1} \\\sqrt{\dfrac{1}{n + 2}} &\leq \sqrt{\dfrac{1}{n + 1}}\\\dfrac{1}{\sqrt{n + 2}} &\leq \dfrac{1}{\sqrt{n + 1}}\\ a_{n + 1} &\leq a_n\end{aligned}

From this we can see that as the term progresses, the value of $a_n$ decreases. We have now confirmed the first condition, so let’s move on to checking whether $\lim_{n \rightarrow \infty} a_n =0$, where $a_n = \dfrac{1}{\sqrt{n + 1}}$.

\begin{aligned} \lim_{n \rightarrow \infty} \dfrac{1}{\sqrt{n + 1}} &= \lim_{n \rightarrow \infty} \dfrac{1}{\sqrt{n + 1}} \cdot \dfrac{\dfrac{1}{n^2}}{\dfrac{1}{n^2}}\\&= \lim_{n \rightarrow \infty} \dfrac{\dfrac{1}{n^2}}{\dfrac{\sqrt{n + 1}}{n^2}}\\&= \lim_{n \rightarrow \infty} \dfrac{\dfrac{1}{n^2}}{\sqrt{\dfrac{n + 1}{n}}}\\&= \lim_{n \rightarrow \infty} \dfrac{\dfrac{1}{n^2}}{\sqrt{1 +\dfrac{1}{n}}}\\&= \dfrac{0}{\sqrt{1 + 0}}\\&= 0\end{aligned}

We have just shown that the limit of $a_n$ is equal to $0$ as $n$ approaches infinity. Since the series meets the two conditions that the alternating series test requires, the series is convergent.