Convergent series – Definition, Tests, and Examples

When we’re working with different series, one of the important properties of a series we often ask is whether the given series is convergent or not. Learning how to identify convergent series can help us understand a given series’s behavior as they approach infinity.

A series is said to be convergent when it approaches a certain value as the series approaches infinity.

Since we’re working with series in this article, it will be helpful to keep these resources handy in case you need a quick refresher:

• Refresh your knowledge on arithmetic, geometric, and recursive
• Review our knowledge on the nth term test and see how they can be useful.
• Understand what a divergent series is since we normally intertwine these two topics.
• Ensure your knowledge of limits and evaluating limits to understand the technical definition of limits better.

In this article, we’ll focus on understanding what makes convergent series unique. We’ll also learn how we can confirm if a given series is convergent or not. Let’s go ahead and first visualize what it means to have a convergent series.

What is a convergent series?                

Let’s begin this section by visualizing how terms of convergent series appear on a graph.

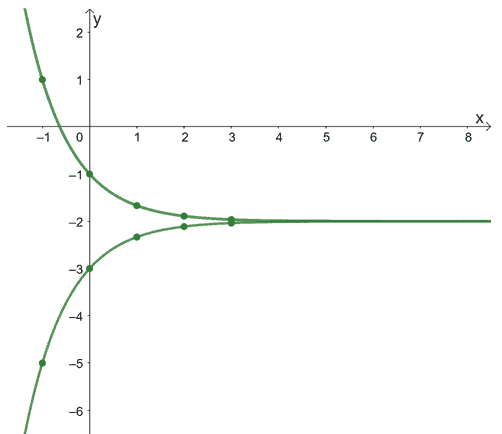
From this, we can see that the series’s partial sums approach a certain number as the value of $n$ increases. This means that the sum of a convergent series will approach a certain value as we add more terms and approach infinity.

Here’s another example that we can use to understand what makes convergent series special. Below is convergent series and a geometric series:

\begin{aligned}\dfrac{1}{3} + \dfrac{1}{9} + \dfrac{1}{27} + \dfrac{1}{81} + … \end{aligned}

Let’s observe how the sum progresses as we add more terms:

From this, we can see that the convergent series approaches $0.50 = \dfrac{1}{2}$ as the partial sums are made up of more terms.

Here’s a quick exercise: try to plot the function $\dfrac{1}{2^x}$ and check if it also converges.

Convergent series definition            

We’ve shown different examples that can help us understand the conceptual idea of convergent series. Now, why don’t we define convergent series technically?

A convergent series exhibit a property where an infinite series approaches a limit as the number of terms increase.

This means that given an infinite series, $\sum_{n=1}^{\infty}a_n = a_1 + a_2 + a_3 + …$, the series is said to be convergent when $\lim_{n \rightarrow \infty}\sum_{n=1}^{\infty}a_n = L$, where $L$ is a constant.

This clearly shows that what makes the convergent series special is that it approaches a constant value as more terms are added to the partial sum.

However, some instances will make inspection tedious and make it impossible for us to confirm a convergence series. When this happens, there are other ways for us to tell when a given series is convergent or not.

How to tell if a series converges?                

We’ve learned in the past how to confirm if a series is divergent using the nth term test, so it’s no surprise to know that there are different methods we can utilize to test if a series converges.

The trick here is to know which method works best for the given series. Check out the summary we’ve prepared for the common tests we can apply, and we’ve included quick notes on when they’re best utilized.

Method 1: Manually Testing the  Partial Sum

The first, of course, is for us to manually add terms and compare their partial sums, as we have shown in our earlier example. This method is best used when the terms are easy to manipulate or have a calculator handy.

As you might guess, it will be a tedious process, especially if we’re working with complex terms and series.

Method 2: Comparison Test

This test is most helpful when we know a series that has been proven to be a convergent series and can be used to prove another series’ convergence.

Let’say we have $0 \leq a_n \leq b_n$ for all values of $n$. The comparison states that:

• If $\sum_{n=1}^{\infty}b_n$ is convergent, the series $\sum_{n=1}^{\infty}a_n$ is also convergent.
• If $\sum_{n=1}^{\infty}a_n$ is divergent, the series $\sum_{n=1}^{\infty}b_n$ is also divergent.

Method 3: Geometric Test

This test can only be used when we want to confirm if a given geometric series is convergent or not.

Let’s say we have $\sum_{n =1}^{\infty}a r^{n – 1}$, where $r$ is the common ratio shared by the series.

• If $|r| < 1$, the series is convergent and is expected to approach $\dfrac{a}{1 – r}$.
• If $|r| \geq 1$, the series is not convergent and is divergent instead.

Method 4: Ratio Test

This test helps find two consecutive terms’ expressions in terms of $n$ from the given infinite series.

Let’s say that we have the series, $\sum_{n=1}^{\infty}a_n$.

• The series is convergent when $\lim_{x \rightarrow \infty} \left | \dfrac{a_{n + 1}}{a_n} \right | <1$.
• The series is divergent when $\lim_{x \rightarrow \infty} \left | \dfrac{a_{n + 1}}{a_n} \right | > 1$.
• When $\lim_{x \rightarrow \infty} \left | \dfrac{a_{n + 1}}{a_n} \right | =1$, we won’t be able to conclude anything.

Method 5: Ratio Test

This test helps find two consecutive terms’ expressions in terms of $n$ from the given infinite series.

Let’s say that we have the series, $\sum_{n=1}^{\infty}a_n$.

• The series is convergent when $\lim_{x \rightarrow \infty} \left | \dfrac{a_{n + 1}}{a_n} \right | <1$.
• The series is divergent when $\lim_{x \rightarrow \infty} \left | \dfrac{a_{n + 1}}{a_n} \right | > 1$.
• When $\lim_{x \rightarrow \infty} \left | \dfrac{a_{n + 1}}{a_n} \right | =1$, we won’t be able to conclude anything.

Method 6: Root Test

The root test has a similar process to the ratio test, but this time, we’re working with the nth term’s roots.

Let’s say that we have the series, $\sum_{n=1}^{\infty}a_n$.

• The series is convergent when $\lim_{x \rightarrow \infty} \sqrt[n]{a_n} <1$.
• The series is divergent when $\lim_{x \rightarrow \infty} \sqrt[n]{a_n} >1$ .
• When $\lim_{x \rightarrow \infty} \sqrt[n]{a_n} =1$, we won’t be able to conclude anything.

There are actually two more commonly applied methods: the alternating series test and the integral test. We’ve allotted a separate article for the alternating series test because of its interesting properties, so make sure to check the articles we wrote about it as well as the alternating series.

We’ve thoroughly discussed what makes a series convergent and the different techniques we can apply to test a series for convergence. It’s now time for us to apply our knowledge and try out these examples shown below.

Example 1

Determine if the following infinite series is converging or not by finding the first four partial sums of each series.

    a. $(-1)^0 + (-1)^1 + (-1)^2 + (-1)^3 + (-1)^4 + …$
    b. $\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{8} + \dfrac{1}{16} …$
    c. $\sum_{n=1}^{\infty}a_n$, where $a_n = \dfrac{1}{n + 2}$

Solution

It’ll be more organized if we summarize the first four partial sums in a table. Why don’t we work on the first item and simply the first four terms.

\begin{aligned}(-1)^0 + (-1)^1 + (-1)^2 + (-1)^3  + … = 1 + (-1) + 1 + (-1) + …  \end{aligned}

We can see that the partial sums alternate between $0$ and $1$, so this series does not converge.

Let’s apply a similar process to for the next series, $\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{8} + \dfrac{1}{16} …$.

From this, we can see that as we progress with the infinite series, we can see that the partial sum approaches $1$, so we can say that the series is convergent.

We can also confirm this through a geometric test since the series a geometric series.

The third series requires more steps since we’ll need to find the values of the first four terms first.

By inspection, we can see that the partial sums increase as more terms are added. If we add more terms, you can also see the partial sums continue increasing.

This means that the partial sum won’t approach a fixed value as more terms are added, so the series is not convergent.

Example 2

Apply different techniques to check if the following series is convergent or not.

    a. $\sum_{n=1}^{\infty} \dfrac{1}{2^n}$
    b. $\sum_{n=1}^{\infty} \dfrac{1}{2^n + 4}$
    c. $\sum_{n=1}^{\infty} \dfrac{3^n}{n!}$

Solution

The first series, $\sum_{n=1}^{\infty} \dfrac{1}{2^n}$, is a geometric series. Why don’t we write down the first four terms?

\begin{aligned}\dfrac{1}{2^1} &= \dfrac{1}{2}\\ \dfrac{1}{2^2} &= \dfrac{1}{4}\\ \dfrac{1}{2^3} &= \dfrac{1}{8}\\\dfrac{1}{2^4} &= \dfrac{1}{16}\\.\\.\\.\end{aligned}

From this, we can see that the common ratio is $\dfrac{1}{2}$. Recall that through the geometric test, since $|r| <1$, the series is convergent.

The second series, $\sum_{n=1}^{\infty} \dfrac{1}{2^n + 4}$, looks similar to the first one, but the difference is that the second expression has a $+4$ in its denominator.

When this happens, we can use the comparison test. To see which of the expression is greater as $n$ increases and when $n \geq 1$, let’s compare their first four terms first.

We can see that the nth term of $\sum_{n=1}^{\infty} \dfrac{1}{2^n + 4}$ are much smaller than the nth term of $\sum_{n=1}^{\infty} \dfrac{1}{2^n}$.This will be true for all terms since $2^n < 2^n + 4$ and consequently, $\dfrac{1}{2^n} > \dfrac{1}{2^n + 4}$.

Since we’ve shown that the series, $\sum_{n=1}^{\infty} \dfrac{1}{2^n}$, is convergent, and $\dfrac{1}{2^n} > \dfrac{1}{2^n + 4}$, we can conclude that the second series is convergent as well.

It will be tedious to find the different terms of the series such as $\sum_{n=1}^{\infty} \dfrac{3^n}{n!}$. But we can immediately find the expressions for the nth term and the term before that.

\begin{aligned}a_{n + 1} &= \dfrac{3^{n +1}}{(n +1)!}\\a_n &= \dfrac{3^n}{n!}\end{aligned}

When we have a series like a root test will be the best option since we can simplify the ratio of $a_{n + 1}$ and $a_n$.

\begin{aligned}\dfrac{a_{n+1}}{a_n} &= \dfrac{\dfrac{3^{n +1}}{(n +1)!}}{\dfrac{3^n}{n!}}\\&= \dfrac{3^{n +1}}{(n +1)!} \cdot\dfrac{n!}{3^n} \\&= \dfrac{3^{n +1}}{3^n} \cdot \dfrac{n!}{(n +1)!}\\&=\dfrac{3^{n +1}}{3^n} \cdot \dfrac{n!}{n!(n +1)}\\&= 3 \cdot \dfrac{1}{n +1}\\&= \dfrac{3}{n +1} \end{aligned}

Now that we have the simplified ratio, $\left | \dfrac{a_{n+1}}{a_n} \right | = \left | \dfrac{3}{n + 1} \right |$, we can find its limit as it approaches infinity.

\begin{aligned}\lim_{n\rightarrow \infty} \left | \dfrac{a_{n+1}}{a_n} \right | &= \lim_{n\rightarrow \infty}\left | \dfrac{3}{n + 1} \right |\\&= 0\\ &<1 \end{aligned}

From this, we can see that the limit of their ratio as $n$ approaches infinity is $0$ and is less than $1$.

According to the ratio test, when $\lim_{n\rightarrow \infty} \left | \dfrac{a_{n+1}}{a_n} \right | < 1$, the series is convergent.

These three examples show that are certain series that will be more compatible with particular convergence tests. This is why familiarizing yourself with the tests and when they’re best used will go a long way in identifying different series’ convergence (and divergence).