Distance Formula – Explanation and Examples

The distance formula is an equation used to calculate the length of a line segment given its endpoints.

Since the inputs for the distance formula are two points, it can also be used to determine the distance between two points.

The distance formula is used for line segments and points in two-dimensional space. It is a good idea to make sure you have a solid understanding of coordinate geometry before moving on with this subject. It is also a good idea to review the Pythagorean Theorem since we can use it to derive the distance formula.

This topic will cover the following subtopics:

• What is the Distance Formula?
• Where did the Formula Come From?
• Deriving the Formula
• How to Use the Distance Formula
• How to Find the Distance Between Two Points

What is the Distance Formula?

If we have two points (x₁, y₁) and (x₂, y₂), the distance between them is:

D=√((x₁-x₂)²+(y₁-y₂)2).

Note that we will get the same answer regardless of which point we choose as (x₁, y₁) and which we choose as (x₂, y₂).

The distance formula tells us the length of a line segment with the given points as endpoints. More generally, it tells us the distance between the two given points.

The distance formula may seem complicated and difficult to remember. Actually, however, the easiest way to keep the plus and minus signs and squares and square roots straight is to remember the origins of the formula.

Where Did the Formula Come From?

The distance formula is actually related to the Pythagorean Theorem!

Why?

Let’s consider a line segment that starts at the origin and ends at the point (3, 4).

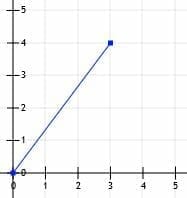
We can then draw lines from (0, 0) to (3, 0) and from (3, 0) to (3, 4).

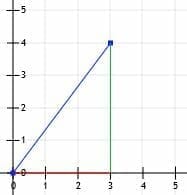
We now have a right triangle! Since the legs of this triangle are precisely horizontal and vertical and since they intersect grid lines, we can just count their lengths. The horizontal line is 3 units, and the vertical line is 4 units.

Then, we know this is a special 3-4-5 triangle, and the length of the horizontal line is 5 units.

But, if we consider how we constructed this triangle, we realize that every line segment can be modeled as the hypotenuse of a right triangle.

Deriving the Formula

Therefore, we can use the Pythagorean Theorem to derive the distance formula.

If the Pythagorean Theorem is a²+b²=c², where a is the horizontal line and b is the vertical line in this case, then the length of the hypotenuse, c, is:

√(a²+b²).

The length of any horizontal line is the difference between the two x-values in two points. In our initial example, for instance, the difference is 0-3=3 units. Likewise, the length of any vertical line is the difference between the two y-values. Again, in our initial example, the length was 4-0=4 units.

Therefore, we can replace a with x₁-x₂ and b with y₁-y₂ to get:

C=√(((x₁-x₂))²+((y₁-y₂))²).

This is the distance formula!

How to Use the Distance Formula

We can use the distance formula to find the length of a line segment or the distance between two points.

First, if we do not already know the coordinates of the line segment’s endpoints or the two points in question, we have to find those.

Recall that the coordinates of a point are simply (x, y), where x and y are real numbers representing the horizontal distance from the origin and the vertical distance from the origin respectively. Negative numbers represent movement left and down, while positive numbers represent movement up and to the right.

Coordinate planes will usually have grid lines representing a fixed interval. This can be 1 unit, 2 units, pi units, 100 units, etc. It can also be different for horizontal and vertical grid lines. Always check the grid line interval length before determining the coordinates of a point.

Then, finally, we can figure out a particular point’s x-coordinate by counting the number of vertical grid lines between it and the origin and then multiplying that number by the grid line interval length. Likewise, the y-coordinate is the number of horizontal grid lines between it and the origin multiplied by the interval length.

How to Find the Distance Between Two Points

Now, pick one of the points to be (x₁, y₁), and let the other be (x₂, y₂).

We can determine the distance between these two points by simply plugging the numbers in to the distance formula.

Remember, it doesn’t matter which point you select as (x₁, y₁) and which point you select as (x₂, y₂). Since the distance formula involves squaring the difference, it doesn’t matter if we have x₁-x₂ or x₂-x₁ because (x₁-x₂)²=(x₂-x₁)². In fact, expanding both equations gives us x₁²+x₂²-2x₁x₂. The same is true for y₁ and y₂.

Note that, in the special case where one of the points is the origin, the distance formula simplifies to:

D=√(x²+y²).

Examples

In this section, we will go over common problems involving the distance formula as well as the step-by-step solutions to these problems.

Example 1

Find the coordinates of the vertices of the triangle shown. Then, use the distance formula to find the perimeter of the triangle.

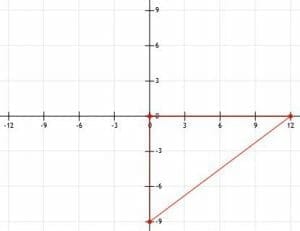
Example 1 Solution

Because this is a right triangle, we could actually just find the lengths of the horizontal and vertical lines. Then, we could find the length of the hypotenuse using the Pythagorean Theorem. However, we will use the distance formula in this solution to get some practice with it.

Let’s consider the horizontal line first. Let the origin be (x₁, y₁) and let the point (12, 0) be (x₂, y₂). Then, plugging in the values, we have:

D=√((0-12)²+(0-0)²).

This simplifies as:

D=√((12)²+0).

D=√(144).

Finally, we know D=√(144)=12. Therefore, the length of the horizontal line is 12 units.

Likewise, if the origin is (x₁, y₁) and the point (0, -9) is (x₂, y₂), we have:

D=√((0-0)²+(0+9)²)

D=√(81)

Thus, we can conclude that D=√(81)=9 units, and this is the length of the vertical line.

Finally, let (12, 0) be (x₁, y₁) and let (0, -9) be (x₂, y₂). The length of the hypotenuse is therefore:

D=√((12-0)²+(0+9)²)

D=√(144+81)

We can further simplify this to:

D=√(225)=15.

Therefore, the lengths are 8 units, 9 units, and 15 units. The perimeter of the triangle is 8+9+15=32.

What if we had just found the length of the horizontal and vertical lines and then used the Pythagorean Theorem? We would have had 8²+9²=64+91=225. The square root of 225 is 15, so either way works for getting the answer.

Example 2

Compare the lengths of four line segments with a common endpoint at the origin. Line A ends at (7, 16), line B ends at (-7, 16), line C ends at (-7, -16), and line D ends at (7, -16).

Example 2 Solution

A quick sketch graphically shows us that these four segments all have the same length.

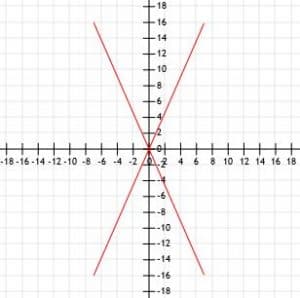
Let’s use the distance formula and see if we get the same results.

Line A:

Let the origin be (x₁, y₁) and let (7, 16) be (x₂, y₂). Then, we have:

D=√((0-7)²+(0-16)²)

D=√(49+256)

This is equivalent to:

D=√(305)

Since 305=5×61, this number is in simplest form.

Line B:

Let the origin be (x₁, y₁), and let (-7, 16) be (x₂, y₂). Then, we have:

D=√((0+7)²+(0-16)²)

D=√(49+256)

As before, then, D=√(305).

Line C:

Once again, let (x₁, y₁) be the origin and (-7, -16) be (x₂, y₂). The distance is:

D=√((0+7)²+(0+16)²)

D=√(49+256)

Again, the distance is D=√(305).

Line D:

Finally, let (x₁, y₁) be the origin and let (7, -16) be (x₂, y₂). The distance is:

D=√((0-7)²+(0+16)²)

D=√(49+256)

Like the other lines, D’s distance is D=√(305).

This example Illustrates both the fact that the distances do not have to be whole numbers and that, since the horizontal and vertical differences are squared in the formula, the order of the numbers is not very important.

Example 3

Find the distance between the points (-8, 3) and (5, 6).

Example 3 Solution

Let’s let (-8, 3) be the point (x₁, y₁), and let (5, 6) be (x₂, y₂).

Then, plugging the values into the formula gives us:

D=√((-8-5)²+(3-6)²)

D=√(13²+3²)

Simplifying further gives us

D=√(169+9)

D=√(178)

Since 178=2×89, √(178) cannot be further simplified. Therefore, this is the distance between the two points.

Example 4

Find perimeter of the triangle with end points ABC, where A=(1, 2), B=(-3, 4), and C=(-1, -5).

Example 4 Solution

We have to first find the lengths of AB, BC, and AC, and then add them up.

AB:

Let A be (x₁, y₁), and let B be (x₂, y₂). AB is:

D=√((1+3)²+(2-4)²)

D=√((4²+2²)

This further simplifies to:

D=√(16+4)

D=√(20)

Since 20 is divisible by 4, √(20)=√(4×5)=√(4)×√(5)=2√(5).

BC:

Let B be (x₁, y₁) and let C be (x₂, y₂). The distance is:

D=√((-3+1)²+(4+5)²)

D=√((-2)²+(9)²)

This is:

D=√(4+81)

D=√(85)

Since 85=17×5, √(85) cannot be simplified and is the length of the segment.

AC:

Let A be (x₁, y₁), and C be (x₂, y₂). The length of the line segment is:

D=√((1+1)²+(2+5)²)

D=√((2)²+(7)²)

This simplifies to:

D=√(4+49)

D=√(53)

Since 53 is prime, this length is √(53).

Therefore, the perimeter is√(53)+√(5)+2√(5). It’s okay to leave this number as is. Rounding to the nearest hundredth, however, gives us 20.97.

Example 5

The lines A and B have the same distance. If A has coordinates at (8, 2) and (-3, -4) and B has coordinates at (6, 4) and (7, c), what is the value of c?

Example 5 Solution

In this case, we will have to find the length of A and then work backwards to find the value of c.

Let (8, 2) be (x₁, y₁), and let (-3, -4) be (x₂, y₂).

Then, the length of A is:

D=√((8+3)²+(2+4)²)

D=√(11²+6²)

Simplifying further gives us

D=√(121+36)

D=√(157)

Since 157 is prime, this is the length of A.

Now, since we already know the length of B and three of the four coordinates, we can plug in the values we know. Let (6, 4) be (x₁, y₁), and let (7, c) be (x₂, y₂).

√(157)=√((6-7)²+(4-c)²)

√(157)=√(1+(4-c)²)

Squaring both sides gives us:

157=1+(4-c)².

156=(4-c)².

Now, we take the square root of both sides to get:

√(156)=4-c.

Therefore, 4-√(156)=c. Since 156 is divisible by 4, this can be further simplified to c=4(1-√(39)).

Example 6

A farmer looks at a survey of his property. He wants to build a new fence that extends from a point one-half acre east and one-fourth of an acre north of the southwest corner of his property to a point two acres east and one and a half acres north of the southwest corner of his property. What is the length of the fence?

Example 6 Solution

First, we need t convert the fence’s endpoints to coordinates. Let’s let the southwest corner of the property be the reference point and east and north be the positive direction. Therefore, the starting point for the fence is (½, ¼). Let’s call this (x₁, y₁). The ending point, (x₂, y₂) is (2, ³/₂).

The length of the fence is therefore:

D=√((¹/₂-2)²+(¹/₄–³/₂)²)

D=√((-³/₂)²+(-⁵/₄)²)

Squaring the numerator and denominator of the improper fractions gives us:

D=√(⁹/₄+²⁵/₁₆)=√(³⁶/₁₆+²⁵/₁₆).

This is:

√(⁶¹/₁₆).

We can rewrite this as ¹/₄√(61) acres.