Logarithm Rules – Explanation & Examples

What is a logarithm? Why do we study them? And what are their rules and laws?

To start with, the logarithm of a number ‘b’ can be defined as the power or exponent to which another number ‘a’ must be raised to produce the result equal to the number b.

We can represent this statement symbolically as;

log _a b = n.

Similarly, we can define the logarithm of a number as the inverse of its exponents. For instance, log _a b = n can be represented exponentially as; a ⁿ = b.

Therefore, we can conclude that;

aⁿ = b ⇔ log _a b = n.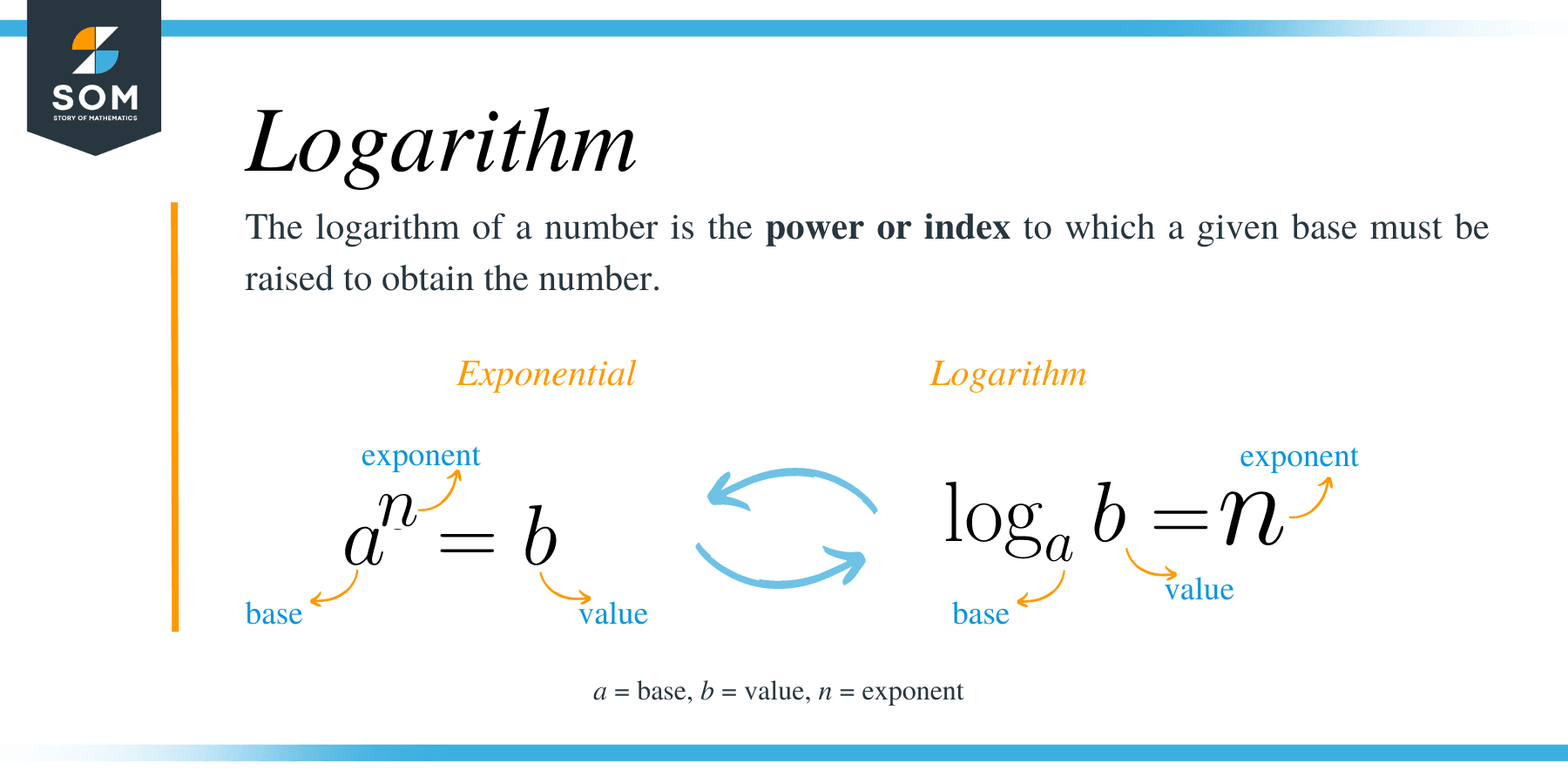

Although logarithms are taught in schools to simplify computation involving large numbers, they still have a significant role in our daily lives.

Let’s see some of these applications of logarithms:

• We use logarithms to measure the acidity and alkalinity of chemical solutions.
• Measurement of earthquake intensity is performed on the Richter scale using logarithms.
• The level of noise is measured in dB (decibels) on a logarithmic scale.
• Exponential processes such as the decay of ratio active isotopes, growth of bacteria, the spread of an epidemic in a population, and cooling of a dead body are analyzed using logarithms.
• A logarithm is used to calculate the payment period of a loan.
• In calculus, the logarithm is used to differentiate complex problems and determine the area under curves.

Like exponents, logarithms have rules and laws that work the same way as the rules of exponents. It is important to note that the laws and rules of logarithms apply to logarithms of any base. However, the same base must be used throughout a calculation.

We can use laws and rules of logarithms to perform the following operations:

• Changing logarithmic functions to exponential form.
• Addition
• Subtraction
• Multiplication
• Division
• Expanding and condensing
• Solving logarithmic equations.

Laws of logarithms

The logarithmic expressions can be written in different ways but under certain laws called laws of logarithms. These laws can be applied on any base, but during a calculation, the same base is used.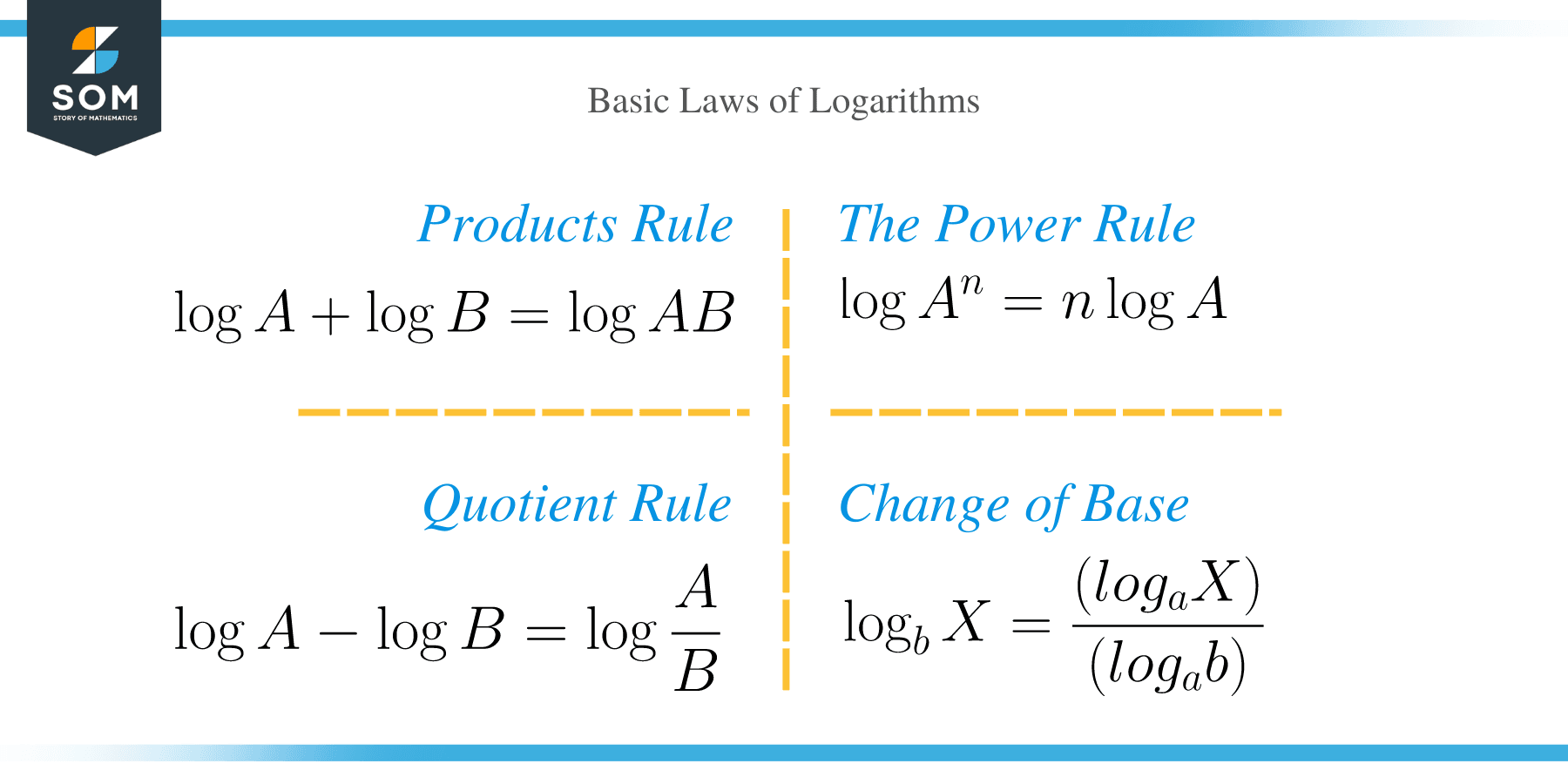

The four basic laws of logarithms include:

The Product Rule Law

The first law of logarithms state that the sum of two logarithms is equal to the product of the logarithms.  The first law is represented as;

⟹ log A + log B = log AB

Example:

1. log ₂ 5 + log ₂ 4 = log ₂ (5 × 4) = log ₂ 20
2. log ₁₀ 6 + log ₁₀ 3 = log ₁₀ (6 x 3) = log ₁₀ 18

• log x + log y = log (x * y) = log xy

1. log 4x + log x = log (4x * x) = log 4x²

The Quotient Rule Law

Subtraction of two logarithms A and B is equal to dividing the logarithms.

⟹ log A − log B = log (A/B)

Example:

1. log ₁₀ 6 – log ₁₀ 3 = log ₁₀ (6/3) = log ₁₀ 2
2. log ₂ 4x – log ₂ x = log ₂ (4x/x) = log ₂ 4

The Power Rule Law

⟹ log A ⁿ = n log A

Example:

1. log ₁₀ 5³ = 3 log ₁₀ 5
2. 2 log x = log x²

• log(4x)³ = 3 log (4x)

1. 5 ln x² = ln x ^{(2 *5)} = ln x¹⁰

Change of Base Rule Law

⟹ log _b x = (log _a x) / (log _a b)

Example 4:

• log ₄16 = (log 16) / (log 4).

Rules of Logarithms

Logarithms are a very disciplined field of mathematics. They are always applied under certain rules and regulations.

Following rules needed to be remembered while playing with logarithms:

• Given that aⁿ= b ⇔ log _a b = n, the logarithm of the number b is only defined for positive real numbers.

⟹ a > 0 (a ≠ 1), aⁿ > 0.

• The logarithm of a positive real number can be negative, zero or positive.

Examples

1. 3²= 9 ⇔ log ₃ 9 = 2
2. 5⁴= 625 ⇔ log ₅ 625 = 4
3. 7⁰= 1 ⇔ log ₇ 1 = 0
4. 2^-3= ¹/₈ ⇔ log ₂ (¹/₈) = -3
5. 10^-2= 0.01 ⇔ log ₁₀01 = -2
6. 2⁶= 64 ⇔ log ₂ 64 = 6
7. 3^{– 4}= 1/3⁴ = 1/81 ⇔ log ₃ 1/81 = -4
8. 10^-2= 1/100 = 0.01 ⇔ log ₁₀01 = -2

• Logarithmic values of a given number are different for different bases.

Examples

1. log ₉ 81 ≠ log ₃ 81
2. log ₂ 16 ≠ log ₄ 16

• Logarithms to the base of 10 are referred to as common logarithms. When a logarithm is written without a subscript base, we assume the base to be 10.

Examples

1. log 21 = log ₁₀
2. log 0.05 = log ₁₀ 05

• Logarithm to the base ‘e’ is called natural logarithms. The constant e is approximated as 2.7183. Natural logarithms are expressed as ln x, which is the same as log _e
• The logarithmic value of a negative number is imaginary.
• The logarithm of 1 to any finite non-zero base is zero.
  a⁰=1 ⟹ log _a 1 = 0.

Example:

7⁰ = 1 ⇔ log ₇ 1 = 0

• The logarithm of any positive number to the same base is equal to 1.

a¹=a ⟹ log _a a=1.

Examples

1. log ₁₀ 10 = 1
2. log ₂ 2 = 1

• Given that, x = log _aM then a ^{log a M} = a

Example 1

Evaluate the following expression.

log ₂ ​8 + log ₂ ​4

Solution

Applying the product rule law, we get;

log ₂ ​8 + log ₂ ​4 = log ₂ (8 x 4)

= log ₂ 32

Rewrite 32 in exponential form to get the value of its exponent.

32 = 2⁵

Therefore, 5 is the correct answer

Example 2

Evaluate log ₃ ​162 – log ₃ 2

Solution

This is a subtraction expression; therefore, we apply the quotient rule law.

log ₃ ​162 – log ₃ 2 = log ₃ (162/2)

= log ₃ 81

Write the argument in exponential form

81 = 3 ⁴

Hence, the answer is 4.

Example 3

Expand the logarithmic expression below.

log ₃ ​ (27x ² y ⁵)

Solution

log ₃ ​ (27x ² y ⁵) = log ₃ 27 + log ₃ x² + log ₃ y⁵

= log ₃ (9) + log ₃ (3) + 2log ₃ x + 5log ₃ y

But log ₃ 9 = 3

Substitute to get.

= 3 + log ₃ (3) + 2log ₃ x + 5log ₃ y

Example 4

Calculate the value of log_√2 64.

Solution

⟹ log_√264 = log_√2 (2)⁶

⟹ log_√264 = 6log_√2(2)

⟹ log_√264 = 6log_√2(√2)²

⟹ log_√264= 6 * 2log_√2(√2)

⟹ log_√264 = 12 * 2(1)

⟹ log_√264 = 12

Example 5

Solve for x if log _0.1 (0.0001) = x

Solution

⟹ log_0.1(0.0001) = log_0.1(0.1)⁴

⟹ log_0.1(0.0001) = 4log_0.10.1

⟹ log_0.1(0.0001) = 4(1)

⟹ log_0.1(0.0001) = 4

Therefore, x = 4.

Example 6

Find the value of x given, 2log x = 4log3

Solution

2logx = 4log3

Divide each side by 2.

⟹ log x = (4log3) / 2

⟹ log x = 2log3

⟹ log x = log3²

⟹ log x = log9

x = 9

Example 7

Evaluate log ₂ (5x + 6) = 5

Solution

Rewrite the equation in exponential form

2⁵ = 5x + 6

Simplify.

32 = 5x + 6

Subtract both sides of the equation by 6

32 – 6 = 5x + 6 – 6

26 = 5x

x = 26/5

Example 8

Solve log x +log (x−1) = log (3x + 12)

Solution

⇒ log [x (x − 1)] = log (3x + 12)

Drop the logarithms to get;

⇒ [x (x − 1)] = (3x + 12)

Apply the distributive property to remove brackets.

⇒ x² – x = 3x + 12

⇒ x² – x – 3x – 12 = 0

⇒ x² – 4x – 12 = 0

⇒ (x−6) (x+2) = 0

⇒x = − 2, x= 6

Since argument of a logarithm cannot be negative, then the correct answer is x = 6.

Example 9

Evaluate ln 32 – ln (2x) = ln 4x

Solution

ln [32/(2x)] = ln 4x

Drop the natural logs.

[32/ (2x)] = 4x

32/ (2x) = 4x.

Cross multiply.

32 = (2x)4x

32 = 8x²

Divide both sides by 8 to get;

x² = 4

x = – 2, 2

Since, we cannot have the logarithm of a negative number, then x = 2 remains to be the correct answer.

Practice Questions

1. Evaluate log​ ₄ ​​64 + log​ ₄ 16
2. log​ ₃ 14−2log​ ₃ ​​5
3. Evaluate 2 log₃5 + log₃ 40 – 3 log₃ 10
4. Condense log ₂4 + log ₂ 5
5. Expand log₃(xy³/√z)
6. Condense the following expression 5 ln x + 13 ln (x³+ 5) – 1/2 ln (x + 1)
7. Simplify log _a28 – log _a 4 as a single logarithm
8. Solve for the value of log ₅ 8 + ₅ (1/1000)
9. Solve for x in the logarithm 3log ₅ 2 = 2log ₅ X
10. Rewrite log12 + log 5 as a single logarithm