- Home
- >
- Parametrize a circle – Equations, Graphs, and Examples
Parametrize a circle – Equations, Graphs, and Examples
 Learning how we can parametrize a circle is helpful, especially when we want to visualize a given object’s position over time. As with other applications of parametric equations, it can help us model relationships that do not necessarily function themselves.
Learning how we can parametrize a circle is helpful, especially when we want to visualize a given object’s position over time. As with other applications of parametric equations, it can help us model relationships that do not necessarily function themselves.
We can parametrize a circle by expressing $\boldsymbol{x}$ and $\boldsymbol{x}$ in terms of cosine and sine, respectively.
We’ve already learned about parametric equations in the past, and this article is an extension of that knowledge – focusing on the process of parametrizing circles. Before we dive right into the essential topic for this article, make sure to review your knowledge on the following:
Review what the general equation for the circle is as a conic section.
Understand how the trigonometric ratios can be obtained on a Cartesian coordinate system.
Ready to learn more? Let’s go ahead and begin by reviewing what we know of parametric equations and see how we can apply these to circles.
How to parametrize a circle?
When given an equation in rectangular form, we can express $x$ and $y$ as a function of $t$. The new element, $t$, is now our new parameter, hence, the name of the relationship shared by $x$, $y$, and $t$.
\begin{aligned}x &= f(t)\\y&= g(t)\end{aligned}
This means that we can rewrite the equation of the circle, $x^2 + y^2 = r^2$, in terms of $t$. We can do this by assigning a special function for $x$ and $y$ – this is where the unit circle and trigonometric ratios enter.
Let’s begin by parametrizing the unit circle’s equation,$x^2 + y^2 = 1$, before generalizing the rules.
Parametrizing a Unit Circle
Recall that when $0 \leq t \leq 2\pi$, we can use the expression $x$ and $y$ in terms of cosine and sine.
\begin{aligned}x &= \cos t\\y &= \sin t\end{aligned}
If we square both sides of the equation and add the two, we’ll develop the unit circle’s parametric form.
\begin{aligned}x^2 &= \cos^2 t\\y &= \sin^2 t\\\\x^2 + y^2 &=1\\\cos^2 t + \sin^2 t &= 1\end{aligned}
Parametrizing a Circle Centered at $\boldsymbol{(0, 0)}$
We can extend this concept with circles centered at the origin but with a radius $r$.This means that $r$ will now be a factor of the parametric forms of $x$ and $y$, as shown below.
\begin{aligned}x&= r\cos t\\y&= r\sin t\end{aligned}
Squaring both equations, we’ll be able to come up with the parametric form of the circle’s equation.
\begin{aligned}x^2 &= r^2\cos^2 t\\y &= r^2\sin^2 t\\x^2 + y^2 &= r^2\\r^2(\cos^2 t + \sin^2 t) &= r^2\end{aligned}
The third case we’ll have to consider is parametrizing a circle that is not centered at the origin.
Parametrizing a Circle Centered at $\boldsymbol{(h, k)}$
Since the $x$ and $y$ coordinates are translated along $h$ and $k$ units, respectively, we’ll have to consider these for the parametrized form of the circle’s equation.
\begin{aligned}x -h&= r\cos t\\x &= h+ r\cos t\\y – k&= r\sin t\\y &= k + r\sin t\end{aligned}
Let’s square both sides of the equation and observe how the equation’s parametric would look.
\begin{aligned}(x- h)^2 &= r^2\cos^2 t\\(y -k)^2 &= r^2\sin^2 t\\\\(x- h)^2 + (y- k)^2 &= r^2\\r^2(\cos^2 t + \sin^2 t) &= r^2\end{aligned}
Now that we know how we can parametrize a circle’s equation, why don’t we see how this affects the graph of the equations?
Graphing the parametric equations of a circle
Parametric equations are best used when we want to account for the direction of the curve. These are some quick pointers to remember when graphing the parametric curve of a circle.
Take note of the assigned interval for $t$.
Assign key values of $t$ and use these values to find the corresponding values of $x$ and $y$.
Plot the parametric curve and account for the circle’s direction based on the resulting table of values.
Why don’t we try graphing the parametric equations shown below and the assigned intervals for $t$.
\begin{aligned}x &= 2\cos t\\y&= 2\sin t\\0&\leq t\leq 2\pi\end{aligned}
We begin by assigning key values for $t$ between the interval, $0\leq t\leq 2\pi$, such as $t = \left\{0, \dfrac{\pi}{2}, \pi, \dfrac{3\pi}{2}\right\}$.
$\boldsymbol{t}$ | $\boldsymbol{x = 2\cos t}$ | $\boldsymbol{y = 2\sin t}$ |
$0$ | \begin{aligned}x &= 2\cos 0\\&=2 \end{aligned} | \begin{aligned}y &= 2\sin 0\\&=0 \end{aligned} |
$\dfrac{\pi}{2}$ | \begin{aligned}x &= 2\cos \dfrac{\pi}{2}\\&=0 \end{aligned} | \begin{aligned}y &= 2\sin \dfrac{\pi}{2}\\&= 2 \end{aligned} |
$\pi$ | \begin{aligned}x &= 2\cos \pi\\&=-2 \end{aligned} | \begin{aligned}y &= 2\sin \pi\\&=0 \end{aligned} |
$\dfrac{3\pi}{2}$ | \begin{aligned}x &= 2\cos \dfrac{3\pi}{2}\\&=0 \end{aligned} | \begin{aligned}y &= 2\sin \dfrac{3\pi}{2}\\&= -2 \end{aligned} |
This means that the arrows will be in counterclockwise direction starting from $(2, 0)$ to $(-2, 0)$ then back to $(2, 0)$. We can now graph the parametric equations and let’s not forget to include the arrows to reflect the direction of the curve.
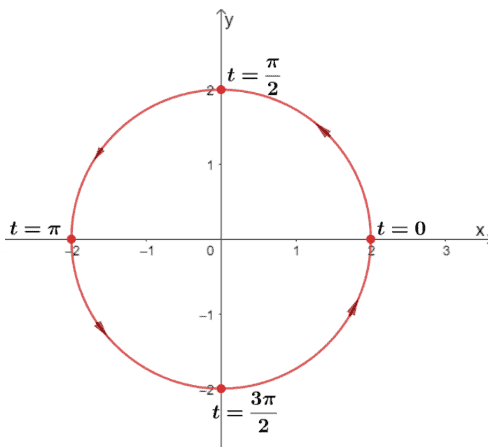
This graph shows the importance of parametric equations – we can graph the motions of objects while accounting for a third parameter – $t$. We’ll apply similar approaches when graphing other circles using their parametric equations.
Example 1
Write two sets of parametric equations for the following rectangular equations.
a. $x^2 + y^2 = 64$
b. $x^2 + y^2 = 12$
c. $(x – 3)^2 + (y + 2)^2 = 81$
d. $(x + 6)^2 + (y – 4)^2 = 24$
Solution
The equation, $x^2 + y^2 = 64$, is a circle centered at the origin, so the standard form the parametric equations representing the curve will be \begin{aligned}x &=r\cos t\\y &=r\sin t\\0&\leq t\leq 2\pi\end{aligned}, where $r$ represents the radius of the circle.
Since $r^2 = 64$, the value of the circle’s radius is equal to $r= 8$. Hence, we have the parametric equations shown below. We’ve also included the interval for $t$.
\begin{aligned}x &=8\cos t\\y &=8\sin t\\0&\leq t \leq 2\pi\end{aligned}
We’ll apply a similar process in writing the parametric equations of $x^2 + y^2 = 12$, but this time, we have $r^2 = 12$ and consequently, $r = 2\sqrt{3}$.
\begin{aligned}x &=2\sqrt{3}\cos t\\y &=2\sqrt{3}\sin t\\0 &\leq t\leq 2\pi\end{aligned}
For the third equation,$(x – 3)^2 + (y + 2)^2 = 81$, the circle is now centered at $(3, -2)$, so we must also translate the parametric equations accordingly.
We’ll use the equations, $\left\{\begin{matrix}x =h + r\cos t\\y =k + r\sin t\end{matrix}\right.$, this time, where $(h, k)$ represents the circle’s center. For our rectangular equation,we also have $r^2 = 81$, so $r = 9$.
\begin{aligned}x &=3 + 9\cos t\\y &=-2 + 9\sin t\\0&\leq t\leq 2\pi\end{aligned}
The fourth equation,$(x + 6)^2 + (y – 4)^2 = 12$, looks similar to the third one, so we’ll use $(h,k) = (-6, 4)$. Since $r^2 = 24$, we can use $r =2\sqrt{6}$.
\begin{aligned}x &=-6 + 2\sqrt{6}\cos t\\y &=4 + 2\sqrt{6}\sin t\\0&\leq t\leq 2\pi\end{aligned}
Hence, we’ve shown how we can write an equation of a circle into its parametric form.
Example 2
Write two sets of parametric equations for the following rectangular equations. Use the resulting parametric equations to graph the circle (we’ll assume that $0 \leq t\leq 2\pi$).
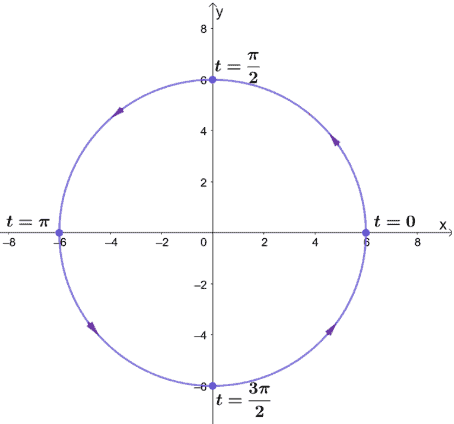
a. $x^2 + y^2 = 36$
b. $(x + 3)^2 + (y – 1)^2 = 16$
Solution
Since the first rectangular equation shows a circle centered at the origin, the standard form of the parametric equations are$\left\{\begin{matrix}x =r\cos t\\y =r\sin t\\0\leq t\leq 2\pi\end{matrix}\right.$. We have $r^2 = 36$, so $r = 6$.
Hence, the circle’s parametric equations are as shown below.
\begin{aligned}x &=6\cos t\\y &=6\sin t\\0&\leq t\leq 2\pi\end{aligned}
To graph this set of parametric equations, let’s use key values of $t$ as guides to know how the parametric curve behaves.
$\boldsymbol{t}$ | $\boldsymbol{x = 6\cos t}$ | $\boldsymbol{y = 6\sin t}$ |
$0$ | \begin{aligned}x &= 6\cos 0\\&=6 \end{aligned} | \begin{aligned}y &= 6\sin 0\\&=0 \end{aligned} |
$\dfrac{\pi}{2}$ | \begin{aligned}x &= 6\cos \dfrac{\pi}{2}\\&=0 \end{aligned} | \begin{aligned}y &= 6\sin \dfrac{\pi}{2}\\&= 6 \end{aligned} |
$\pi$ | \begin{aligned}x &= 6\cos \pi\\&=-6 \end{aligned} | \begin{aligned}y &= 6\sin \pi\\&=0 \end{aligned} |
$\dfrac{3\pi}{2}$ | \begin{aligned}x &= 6\cos \dfrac{3\pi}{2}\\&=0 \end{aligned} | \begin{aligned}y &= 6\sin \dfrac{3\pi}{2}\\&= -6 \end{aligned} |
This means that the parametric curve’s direction is counterclockwise, from $(6,0)$ when $t = 0$, $(0,-6)$ when $t = \dfrac{3\pi}{2}$, then back to $(6,0)$ when $t = 2\pi$.
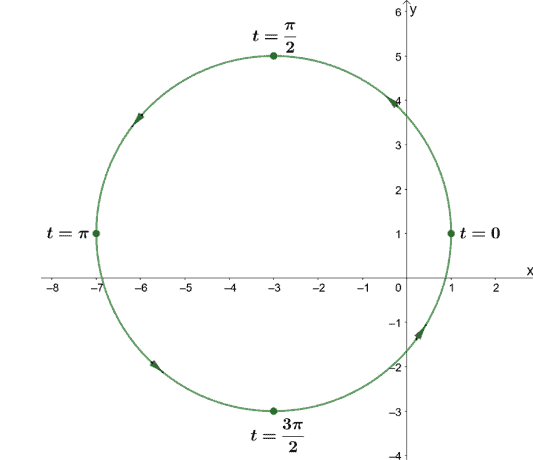
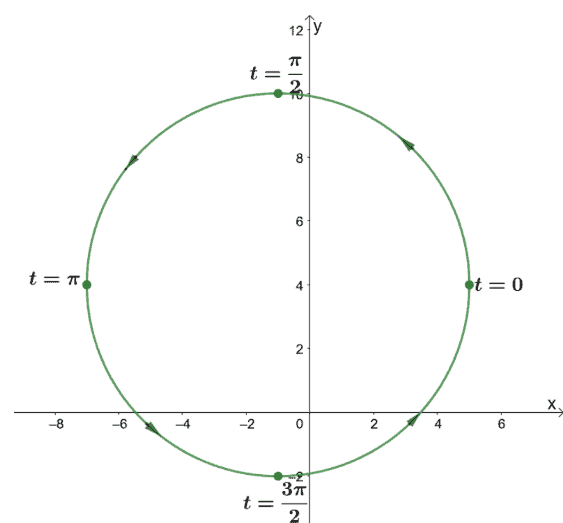
Now, for the second equation,$(x + 3)^2 + (y – 1)^2 = 16$ , we can see that the circle has a radius of $4$ and is centered at $(-3, 1)$. We’ll use these components to rewrite the equation in their parametric forms.
\begin{aligned}x &=h + r\cos t\\y &=k + r\sin t\\\\x &=-3 + 4\cos t\\y &=1 + 4\sin t\phantom{x}\end{aligned}
To graph the parametric curve, we’ll once again use the same interval, $0\leq t\leq 2\pi$, and select key values for $t$ as shown in the table of values below.
$\boldsymbol{x = -3 + 4\cos t}$ | $\boldsymbol{y =1 + 4\sin t}$ | |
$0$ | \begin{aligned}x &= -3 +4\cos 0\\&= -3+4\\&= 1 \end{aligned} | \begin{aligned}y &= 1 +4\sin 0\\&=1 +0\\&=1 \end{aligned} |
$\dfrac{\pi}{2}$ | \begin{aligned}x &= -3 +4\cos \dfrac{\pi}{2}\\&=-3 +0\\&= -3 \end{aligned} | \begin{aligned}y &= 1+ 4\sin \dfrac{\pi}{2}\\&= 1+4\\&=5 \end{aligned} |
$\pi$ | \begin{aligned}x &= -3 +4\cos \pi\\&=-3- 4\\&= -7 \end{aligned} | \begin{aligned}y &= 1+4\sin \pi\\&=1 + 0\\&=1\end{aligned} |
$\dfrac{3\pi}{2}$ | \begin{aligned}x &= -3 +4\cos \dfrac{3\pi}{2}\\&=-3+0\\&= -3 \end{aligned} | \begin{aligned}y &= 1+ 4\sin \dfrac{3\pi}{2}\\&= 1-4\\&= -3 \end{aligned} |
This means that the parametric curve will pass through these points in this order:$(1,1)\rightarrow (-3, 5)\rightarrow (-7,1) \rightarrow (-3, -3)\rightarrow (1, 1)$, in counterclockwise direction.
Practice Questions
![]()
Open Problems
From the last two problems, use the resulting parametric equations to graph the circle (we’ll assume that $0 \leq t\leq 2\pi$).
1. $x^2 + y^2 = 9$
2. $(x + 1)^2 + (y – 4)^2 = 36$
Open Problem Solutions
1.
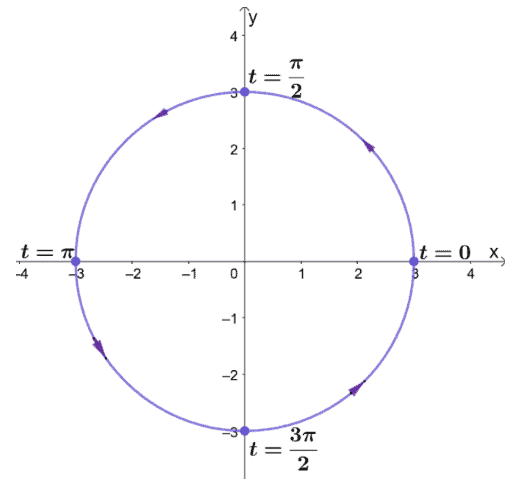
2.
Images/mathematical drawings are created with GeoGebra.
