Polynomial Equation – Properties, Techniques, and Examples

The first few equations you’ll learn to solve in an Algebra class is actually an example of polynomial equations. These equations come in different forms and rules, so it’s essential that we thoroughly understand what they are and what they represent, and how we can manipulate these equations are important.

Polynomial equations are equations that contain polynomials on both sides of the equation.

Since we’re dealing with polynomials and polynomial functions, make sure to check out our article on polynomial functions.

Polynomial equations such as quadratic functions are often used in modeling motions, real-world functions, and extensive technology and science applications. This is also why we need to understand how we can identify and solve polynomial equations.

What is a polynomial equation?

Polynomial equations are equations that contain polynomial expressions on both sides of the equation. Here’s the standard form of a polynomial equation.

Note that  a­_n, a_n-1, … a_o can be any complex number, and the exponents can only be whole numbers for these to be considered polynomial expressions.

 Having an equal sign followed by another polynomial expression makes the polynomial equation distinct from polynomial expressions.

As can be confirmed from the equation shown above, the polynomial equation is said to be in standard form when the terms are arranged from the term with the highest power to the one with the lowest power.

Polynomial equation definition and examples

Polynomial equations contain polynomial expressions, so properties of polynomial functions will still apply. In fact, the degree and the number of terms of the polynomial expression can also help us classify polynomial equations.

Let’s go ahead and take a look at the common types of polynomial equations we may encounter based on the degree:

How to solve polynomial equations?              

A great way to visualize polynomial equations is to think of it is as the result of combining different blocks. When the goal is to find the roots, solutions, or solving for the polynomial equation, we must find a way to take each block apart.

Here are some important pointers to remember when solving polynomial equations:

1. If the polynomial equation is still not in its standard form, rewrite the equation so that it is in standard form: all polynomial expressions on the left side and 0 on the right.
2. Simplify the polynomial equation in standard form and predict the number of zeroes or roots that the equation might have.
3. If the polynomial equation is a linear or quadratic equation, apply previous knowledge to solve these types of equations.
4. If the polynomial equation has a three or higher degree, start by finding one rational factor or zero.
5. Take out this factor and repeat the same process until you’re left with a linear equation or a constant.
6. List down all the roots or zeros.

Let’s do a quick recap of the different techniques we can apply to achieve Step 3. As mentioned, at this point, we should know how to solve linear and quadratic equations extensively. Don’t worry. This website contains a handful of resources about these two equations in case we need a quick refresher.

Linear Equations

Linear equations are polynomial equations that have a degree of 1.

ax + b = 0

Solving for solutions for this type of equation will require us to isolate the unknown variable on one side of the equation. Master your craft in solving linear equations here.

Quadratic Equations

Quadratic equations are polynomial equations with a degree of 2.

ax² + bx + c = 0

There are different ways we can solve quadratic equations – it mostly depends on the form of the quadratic expression on the right-hand side.

• We can factor quadratic expressions and apply the zero-property.
• Applying special algebraic properties such as the difference of two squares, perfect square trinomial properties, and completing the square.
• Lastly, we can also use the quadratic formula to find the zeroes of quadratic equations.

Polynomial Equations (with a degree of 3 or higher)

Here’s the exciting part: what if we need to find the zeros of the solutions of a polynomial equation with degrees that are 3 or higher?

Some cubic and quartic equations can be factored by grouping and be reduced to equations with a smaller degree. There are times, however, that finding the actual factors can be challenging.

Properties and techniques in solving polynomial equations

Here are important properties of polynomial equations that we’ll need to understand to easily find the real zeros and roots of a polynomial equation.

Real Zeros in a Function

The number of real zeroes a polynomial function can have is the same value of the degree. What does this mean? If f(x) has a degree of 5, the maximum number of real zeroes it can have is 5.

Descartes’ Rule of Signs

This rule is helpful when we need to find the zeroes of a polynomial equation without its graph. What does Descartes’s Rule of Signs do? It tells us the number and position of a polynomial equation’s zeroes.

To apply this rule, we’ll need to observe the signs between the coefficients of both f(x) and f(-x). Let’s say we have f(x) = 2x⁴ – 2x³ – 14x² + 2x + 12.

Count the number of times the coefficients switch signs, and the table below summarizes what the result means:

Let’s apply this with f(x) = 2x⁴ – 2x³ – 14x² + 2x + 12.

f(x) = 2x⁴ – 2x³ – 14x² + 2x + 12
f(-x) = 2x⁴ + 2x³ – 14x² – 2x + 12

From the sign changes in f(x), there can be 2 or 0 positive real zeros. Similarly, from f(-x), there are can also be 2 or 0 negative real zeros.

Rational Zeros Theorem

This theorem will help us narrow down the possible rational zeros of a polynomial function.  Let p contain all the factors of a_n (leading term) and q contain all the factors from a_o (constant term).

The possible rational zeros of the polynomial equation can be from dividing p by q, p/q. Make sure that the list contains all possible expressions for p/q in the lowest form.

Using the same example, f(x) = 2x⁴ – 2x³ – 14x² + 2x + 12, we have p = 2 and q = 12. Let’s go ahead and list down all the possible rational zeros of f(x).

Does this mean f(x) has 14 rational zeros? No, this list tells us that if f(x) has rational zeros, it will come from this list. Meaning, we have reduced the possibilities to a reasonable number from an extensive range of rational numbers.

Applying the Remainder Theorem and Synthetic Division

How do we slowly find rational zeros of f(x) once we have a list of p/q? It’s time that we apply our past knowledge on the remainder theorem, factor theorem, and synthetic division. Make sure to take a quick refresher for these topics by clicking on the links.

• This means that we can try each factor listed and check for the remainder.
• If the remainder is zero, the value of p/q is a root of f(x).
• Use the resulting polynomials and repeat the same process until we have all the f(x) zeros.

Finding the zeros of a polynomial function

Why don’t we apply what we’ve just learned to find the zeros of 2x⁴ – 2x³ – 14x² + 2x + 12 = 0? From the previous section, we’ve seen that f(x)’s list of possible rational zeroes is: ±1/12, ±1/6, ±1/4, ± 1/3, ±1/2, ±2/3, ±1, and  ±2.

Let’s check if x = 1 is a root of f(x) using synthetic division.

1  |  2    -2    -14       2      12

              2       0     -14    -12

_____________________________

       2      0    -14      -12     0

Since the remainder is 0, (x – 1) is a factor of f(x) and x = 1 a solution to the equation. Let’s express f(x) as a factor of (x – 1): f(x) = (x -1)(2x³ – 14x – 12).

Use the resulting cubic expression and find a second root for the equation. Let’s try to see if x = 2 is a root of 2x³ – 14x – 12.

-2  |  2      0     -14      -12

               -4        8        12

__________________________

        2      -4      -6         0

Hence, (x + 2) is a factor of f(x) and x = -2 is a root of the equation. Since we have a quadratic expression, we can factor the expression and solve for the two remaining zeros of the equation.

2x² – 4x – 6 = 0

2(x² – 2x – 3) = 0

x² – 2x – 3 = 0

(x – 3)(x + 1) = 0

x = 3, x = -1

Let’s go ahead and take note of all the zeros we have solved for our polynomial equation: x = 1, x = -2, x = 3, and x = -1. The equation has four zeros, as we have expected since it has a degree of 4.

Apply a similar process when finding the zeros of other polynomial equations.

Here’s a guide to help you summarize and follow through the steps we might need to do when finding the zeroes of a given polynomial equation in standard form:

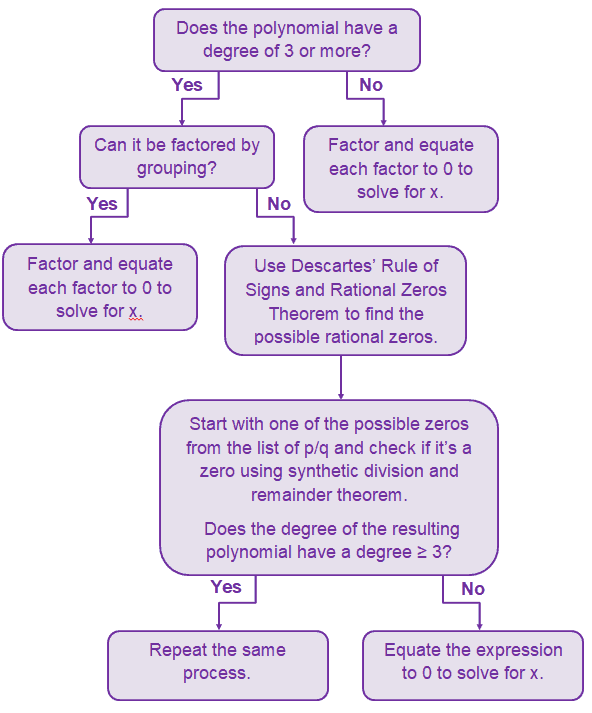
The guide above helps you ask the right questions to ensure we apply the best strategy when solving polynomial equations.

Why don’t we apply this by answering the questions shown below?

Example 1

Given that f(x) = -2x³ + 4x² – 7x – 6, how many sign changes are there in f(x) and f(-x)? Interpret the results.

Solution

We can immediately inspect f(x) for its sign changes. We have two sign changes: -2x³ and 4x² and as +4x² and -7x.

As for f(-x), let’s go ahead and find the expression for f(-x) first.

f(-x) = 2x³ + 4x² + 7x -6

From this, we can see that f(-x) has only one sign change: between 7x and -6. Using Descartes’ Rule of Sign, we can conclude that:

• When f(x) is equated to 0, the resulting equation may have two or zero positive real zeros.
• Similarly, the resulting equation may have one negative real zero.

Example 2

True or False? Given that the polynomial function, g(x), has a degree of 3, the equation g(x) = 0 will always have three real zeros.

Solution

The equation g(x) = 0 will have at most three possible real zeros. This means that it may or may not have three real zeros exactly. One function to further show that the statement is not true is when g(x) = x³ + x.

Let’s solve the equation and observe the results for x. Since the expression is still factorable, we’ll factor x out and equate x² + 1 to 0.

x³ + x = 0

x(x² + 1) = 0

x = 0

x² + 1 = 0

x² = -1

This will only be true when x = -i or x = i. This clearly shows that it is possible for g(x) to not have three real zeros despite having a degree of 3. Hence, the statement is not true.

Example 3

Find the values of x that satisfies the given equation: 4x⁵ – 4x⁴ + 73x² = -18(x -1)+ 73x³.

The equation is still not in its standard form, so let’s go ahead and isolate all terms on the left-hand side.

4x⁵ – 4x⁴ – 73x³ + 73x²+ 18x – 18 = 0

Using the rational zeros theorem, let’s list down the possible rational zeros for the polynomial equation.

Let’s check if x = 1 is a root of f(x) using synthetic division.

1  |  4    -4     -73       73     18     -18

               4        0      -73       0      18

____________________________________

        4      0     -73        0      18       0

Since the remainder is 0, (x – 1) is a factor of the expression and x = 1 is a solution.  Let’s go ahead and try x = 1/2 and x = -1/2 to see if they are zeros of the equation too.

1/2  |  4      0     -73        0         18

                    2        1      -36       -18 

_________________________________

         4        2     -72     -36          0

Make sure to check with resulting polynomial. We now have (x – 1)(x – 1/2)(4x³ + 2x² – 72x – 36) = 0.

-1/2  |  4         2     -72     -36          

                        -2       0       36 

_____________________________

            4        0     -72         0

We can see that x = -1/2 and x = 1/2 are both zeros of the polynomial equation from these two consecutive synthetic divisions.

We now have (x – 1)(x – 1/2)(x + 1/2)(4x² – 72) = 0. Since the remaining expression is a quadratic expression, we can equate it to 0 and solve the polynomial equation’s remaining zeros.

4x² – 72 = 0

4(x² – 18) = 0

x² – 18 = 0

x² = 18

x = ±√18

x = ±2√2

We now have five zeros for the polynomial equation (this is already the maximum number of zeros possible for a polynomial equation with a degree of 5).

Hence, the equation has a solution set of: {-2√2, -1/2, 1/2, 1, 2√2}.