- Home
- >
- Power function – Properties, Graphs, & Applications
JUMP TO TOPIC
Power Function – Properties, Graphs, & Applications
 Ever worked with a function that contains a single term? Chances are, you’ve been working with a power function. This function type is so diverse that if you’re studying functions, we’re 100% sure that you’ve already encountered a type of power function without knowing that it is one.
Ever worked with a function that contains a single term? Chances are, you’ve been working with a power function. This function type is so diverse that if you’re studying functions, we’re 100% sure that you’ve already encountered a type of power function without knowing that it is one.
Why don’t we start with the definition of power functions?
A power function is a single-term function that contains a variable at its base and a constant for its exponent.
This means that there are a lot of parent functions that are also power functions. In this article, we’ll learn:
- The concept behind power functions.
- Special properties that a power function may exhibit.
- Apply these properties in graphing and identifying power functions.
Make sure to have a notepad handy, as this will be a thorough discussion of power functions. We’ll even learn how to apply power functions in word problems.
Why don’t we go ahead and start with its definition and some examples of power functions?
What is a power function?
Before we dive deeper into the power function’s important properties, we should understand the fundamental definition of power functions. Here’s the general form of power functions:
Let’s go ahead and break down this general form and find examples of power functions using this definition.
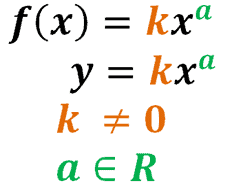
Make sure to familiarize yourself with this form, as we’ll be using this repeatedly throughout the article.
Power functions definition and examples
As shown in the previous section, power functions are functions in the form of f(x) = kxa or y = kxa, where k is a nonzero coefficient, and a is a real number.
Here are some examples of power functions:
- y = -5x2
- y = 2 √x
- f(x) = 3/x2
- g(x) = 2x3
Notice how each function only contains a single term for each example – an important identifier of power functions. The exponents of power functions must also be real numbers, so let’s inspect each exponent from the examples to confirm this.
- The function y = -5x2 and g(x) = 2x3 are functions with whole numbers as their exponents, so they are power functions.
- The square root function, y = 2 √x, can be rewritten as y = 2x1/2, so its exponent is a real number, so it is also a power function.
- We apply the same process with f(x) = 3/x2 and have f(x) = 3x-2 confirming that it is a power function since -2 is a real number.
Below are just some parent functions, and let’s see why they’re all considered power functions as well.
| Parent Function | Function Form |
| Constant Function | y = a |
| Linear Function | y = x |
| Quadratic Function | y = x2 |
| Cubic Function | y = x3 |
| Reciprocal Function | y = 1/ x, y = 1/ x2 |
| Square root Function | y = √x |
Since these parent functions contain one term each and real numbers for their exponents, they are all power functions.
How to graph power functions?
When graphing power functions, we have to keep in mind these two important properties of power functions: their symmetry and end behavior.
Here’s a quick guide on how we graph power functions to show you why these two can help you save time:
- Determine whether the power function is odd or even.
- Apply transformations whenever you can.
- Find some points to help graph half of the power function.
- Apply the symmetry property of the given power function.
- Double-check their end behaviors.
Why don’t we refresh our knowledge on odd and even functions and see how they affect a power function graph?
Even power functions’ symmetry and end behavior
Power functions are either even or odd, so they are also either symmetric about the y-axis and origin. We can also predict the end behavior of power functions based on their coefficient and power.
Let’s observe the graph of these even power functions: y = 2x2 and y = -4x4. To graph each function, plot some points found on the right-side and reflect this curve over the y-axis.
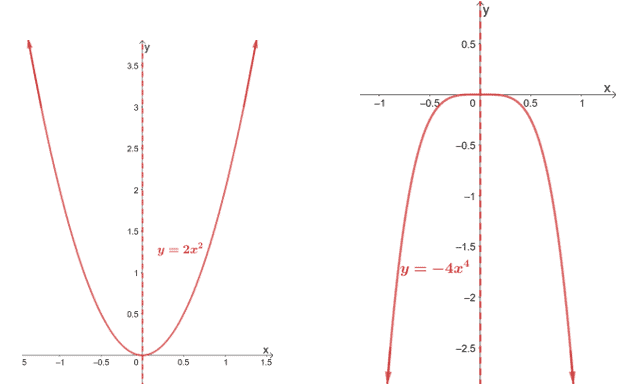
For both graphs, since the exponents are even, the functions are even as well, and consequently, their graphs are symmetric along the y-axis.
Let’s start with even power functions where the coefficient is positive such as y = 2x2.
- Since the coefficient, 2, is positive, the graph is opening upwards.
- We can see that when x < 0, the function is decreasing and when x > 0, the function is decreasing.
- Consequently, both the left and the right side of the curve would be going up (↑).
Now, let’s observe even power functions where the coefficient is negative such as y = -4x4.
- Since the coefficient, -4, is negative, the graph is opening downwards.
- Here, we can see that when x < 0, the function is increasing, and when x > 0, the function is decreasing.
- This means that for both sides, we’re expecting the curve to go down (↓).
Odd power functions’ symmetry and end behavior
How about odd power functions? Let’s go ahead and observe these two functions: y = 3x3 and y = -x5.
To graph the two functions, we can plot some values on either the coordinate plane’s left or right side. Reflect the graph over the origin.
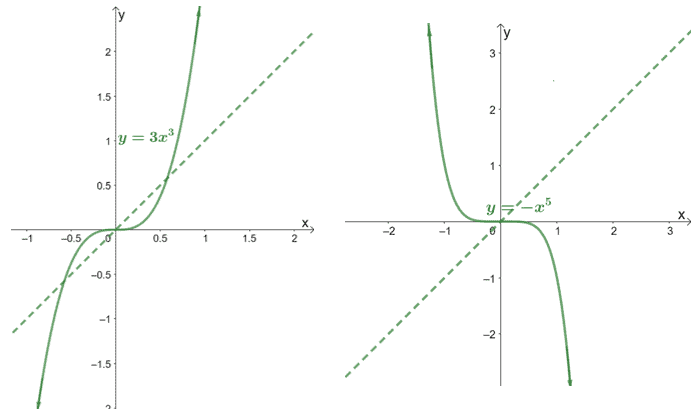
From the definition of odd functions, we can see that both power functions are symmetric about the origin.
Here are some things we can observe based on the graph of y = 3x3, where the coefficient is positive:
- We can see that when x < 0, the function is increasing, and when x > 0, the function increases.
- Consequently, the left side is going down (↓) while the right side is going up (↑).
Let’s now observe the behavior of odd functions when the coefficient is negative.
- We can see that when x < 0 and x > 0, the function is decreasing
- Consequently, the left side is going up (↑) while the right side is going down (↓).
Understanding the effect of the exponent, a
We’ve thoroughly discussed the effects on the graph of a power function based on its parity and the value of k. Now, let’s try to observe the difference when a is a fraction and when a is a whole number.
Case 1: When a = 0 and a = 1, we’re expecting the graph to reduce to a constant function and linear function, respectively.
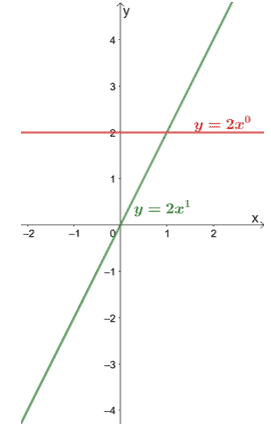
The graphs of y = 2 and y = 2x can confirm this. The same behavior applies to all values of k.
The domain for this case will be all real numbers, or in interval notation, that’s (-∞, ∞).
Case 2: When a < 0. Let’s observe the graphs of y = x-1 and y = x-2:
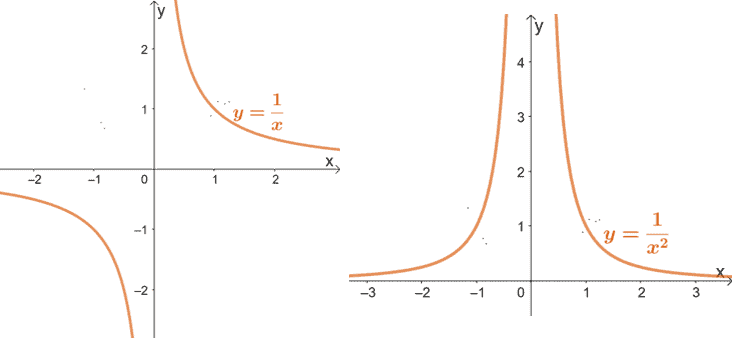
When a is negative, and the power function returns a rational expression, we can see that the graphs approach but are never equal to 0. This means that the domain of these power functions will be any real number except for 0, so the domain is (-∞, 0) U (0, ∞).
The two graphs are also concaving upwards on both sides.
Case 3: When 1< a < 0. Let’s observe the graphs of y = x1/2 and y = x1/3:
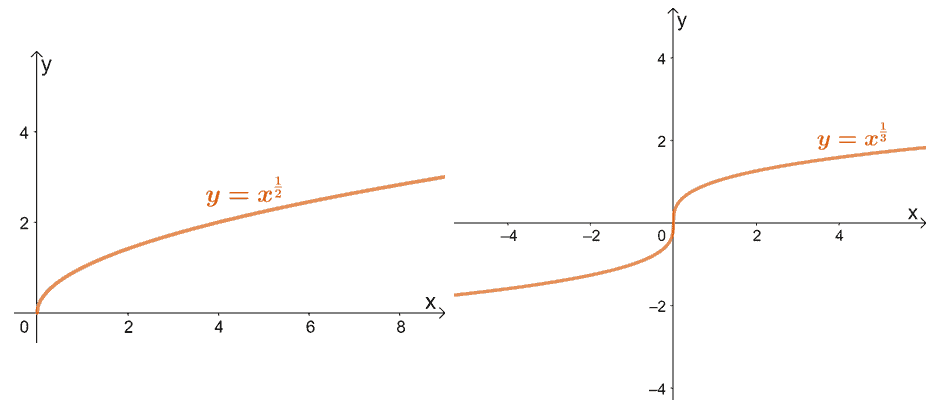
When a is a fraction, and the power function returns a radical expression. We can see that the domain will depend on whether the denominator is even or odd:
- If the denominator is even, only the positive values of x will be part of the domain or [0, ∞).
- If the denominator is odd, its domain can all be real numbers or (-∞, ∞).
The two graphs are also concaving downwards on both sides.
Case 4: When a > 1, let’s observe the graphs of y = x5 and y = x6.
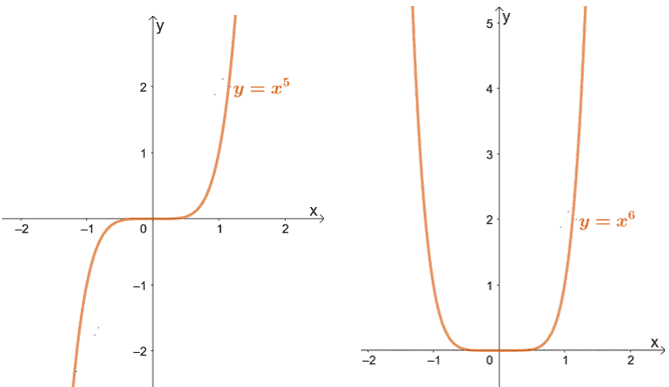
When the exponent is positive, we expect the graphs to be concaving upwards. The domain for this type of power function will be all real numbers or interval notations, (-∞, ∞).
How to find the power function?
Sometimes, we’re given the power function’s graph or some points passing through its graph. We can still find the expression representing the power function using two points.
- Substitute these two points into the general form of power functions, y = kxa.
- Find a way to retain either k or a in one of the equations.
- Determine the values for k and a and substitute them back into the general form of power functions.
Let’s say we want to find the power function that is passing through (2, 16) and (3, 54). Substitute these values into the general form:
| (2, 16) | 16 = k(2)a 16 / 2a = k |
| (3, 54) | 54 = k(3)a 54 / 3a = k |
Let’s equate both right-hand side expressions and have:
16 / 2a = 54 / 3a
8 / 2a = 27 / 3a
23 / 2a = 33 / 3a
2 3 – a = 3 3 – a
This equation will only be true when both sides are equal to 1. This means that 3 – a must be equal to 0. Hence, a = 3.
Substitute this back to either of the expressions of k:
k = 16 / 23
= 16 / 8
= 2
Now that we have a = 3 and k = 2, we can now write the power function expression: y = 2x3.
What if we want to find the expression of the power function based on its graph? Just make sure to look out for two points that the function’s graph passes through, then apply the same process.
Before we try out some more questions involving power functions, why don’t we go ahead and summarize everything that we know so far about power functions?
Summary of power function formulas and their properties
Here are some helpful reminders when working with power functions and their applications:
- When identifying whether a function is a power function, make sure that the expression is a single term, k is a constant, and a is a real number.
- Power functions’ graphs will depend on the value of k and a.
- Apply the properties of odd and even functions whenever applicable.
- When finding the expression for a power function, always utilize the general form, y = kxa.
- Use the table shown below to predict the end behavior of power functions.
| Condition for k | Even power functions | Odd power functions |
| When k > 0 | Function is decreasing when x < 0: As x → – ∞, y → ∞ Function is increasing when x > 0: As x → ∞, y → ∞ | The function is increasing throughout the interval of x: As x → – ∞, y → -∞ As x → ∞, y → ∞ |
| When k < 0 | Function is increasing when x < 0: As x → – ∞, y → – ∞ Function is decreasing when x > 0: As x → ∞, y → – ∞ | The function is decreasing throughout the interval of x: As x → – ∞, y → ∞ As x → ∞, y → – ∞ |
Make sure to understand the concept of power functions and familiarize yourself with the different end behaviors. When you’re ready, let’s go ahead and try out some problems!
Example 1
Which of the following functions are considered power functions?
a. f(x) = -2x2 · 3x
b. g(x) = 2√x + 5
c. h(x) = 0.5xπ
d. m(x) = -(x + 1)2
e. n(x) = 1/ x3
Solution
Inspect each of the given functions and simplify the expressions whenever possible.
a. The function can still be simplified to f(x) = -6x3. We can see that it only contains one term and has a real number for its coefficient and exponent, so f(x) is a power function.
The next two items (b and d) contain more than one term and can’t be simplified, so the functions g(x) and m(x) are not considered as power functions.
c. We always go back to the fundamental definition of power functions: they contain a single term while the coefficient and exponents are real. Both 0.5 and π are real numbers, so h(x) is also a power function.
e. Since 1/ x3 = 1 · x-3, we can see by inspection that it satisfies the conditions of power functions, so n(x) is also a power function.
Hence, the functions in a, c, and e are power functions.
Example 2
Fill in the blanks with always, sometimes, and never to make the following statements true.
a. Cubic functions are ______________ power functions.
b. Constant functions are _____________ power functions.
c. Power functions will ___________ have negative exponents.
Solution
Let’s go ahead and inspect each statement:
a. Some examples of cubic functions are 2x3 and x3 – x2 + x – 1. We can see that the first example is a power function, but the second one is not. This means that cubic functions can sometimes be power functions.
b. The general form of constant functions is y = c, where c is any nonzero constant. We can see from the general form that regardless of the value of c, constant functions will always have a single term with real numbers for their coefficient and exponent. Hence, constant functions will always be power functions.
c. As long as the function contains a single term and a real number exponent, it will be considered a power function. This means that it’s possible to have positive and negative exponents in a power function. So, they may sometimes have negative exponents.
Example 3
Determine the end behaviour of the following power functions:
a. f(x) = x3
b. g(x) = -4x4
c. h(x) = (-3x)3
Solution
When predicting the end behavior of a power function, inspect the sign of the coefficient and the exponent’s value. Use the table we provided to guide you in predicting end behaviors.
a. The function f(x) = x3 has a coefficient of 1 and a positive exponent of 3. Since the power is odd, the function is expected to be increasing throughout its domain.
This means that the left side of its curve is going down while the right-side is going up: (↓↑).
b. For the second function, g(x) = -4x4, has a negative coefficient and an even positive exponent. This means that the graph is expected to open downwards. The function will also be increasing when x < 0 and decreasing when x > 0.
This means that both the left and right sides of the curve are expected to be going down: (↓↓).
c. Let’s simplify the expression for h(x) first: h(x) = -27x3. We can see that h(x) has a negative coefficient and an odd exponent. When this happens, the function is decreasing throughout its domain.
The graph’s curve is going up on the left side and going down on the right side: (↑↓).
Example 4
Show that the product of two power functions will always return a power function as well.
Solution
Let the two power functions be f(x) = mxp and g(x) = nxq, where m and n are real number coefficients. The exponents p and q are real numbers as well.
Multiplying the two functions will result to:
f(x) · g(x) = (mxp) · (nxq)
= mn xp + q
Let mn = k and p + q = a, hence, we have f(x) · g(x) = kxa.
Since mn and p + q are real numbers, k and a will also be real numbers. The product still returned a power function, so we have just confirmed that the two power functions’ product will also be a power function.
Example 5
Graph the power function f(x) = -3x5 and answer the questions that follow.
a. What is the domain and range of the function?
b. If the graph is translated 6 units upward, will the resulting function still be a power function?
Solution
Since f(x) is an odd function, we expect the graph to symmetric about the origin.
| x | f(x) |
| 0 | 0 |
| 1 | -3 |
| 2 | -96 |
We can plot these points to graph half of the curve and reflect it over the origin.
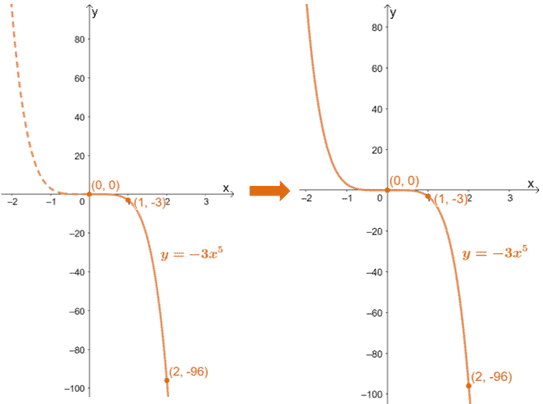
a. Since the exponent is positive and odd, the domain and range of f(x) will be all real numbers or (-∞, ∞). This can also be confirmed by inspecting the graph.
b. When we translate f(x) by 6 units, we add 6 to the expression. Hence, the new function’s expression will now be -3x5 + 6. This expression will contain two terms, and thus, the new function will not be a power function anymore.
Example 6
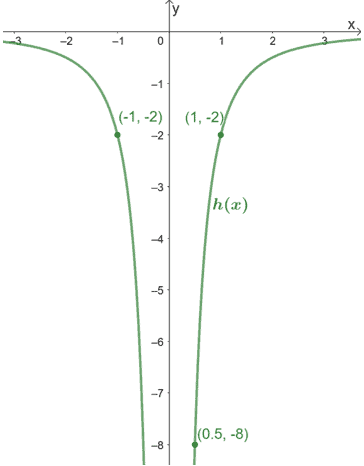
Use the graph shown below to find an expression for h(x).
Solution
Since the graph of h(x) passes through (-1, -2), (1, -2), and (1/2, -8), we can use any of these three points in the general form of the power function: y = kxa.
Notice something about the graph? The curves are approaching but can never be equal to 0, so we’re expecting the exponent to be a fraction.
Let’s substitute (1, -2) first into the power function’s general form. (This will be the best option since k1a will reduce to k.)
-2 = k(1)a
-2 = k
Apply the same process for (1/2, -8), but this time, let’s use k = -2 as well.
-8 = (-2)(-1/2)a
4 = (-1/2)a
(-1/2)-2 = (-1/2)a
For this to be true, a must be equal to -2. Hence, we have h(x) = -2x-2.
Example 7
The power function g(x) passes through the points (4, -6) and (9, -9).
a. What is the expression for g(x)?
b. Graph the function g(x).
c. Find its domain and range, then describe its end behavior.
Solution
Let’s substitute each pair of values into the general form of power functions: y = kxa and simplify the resulting equation.
| (4, -6) | -6 = k(4)a -6= k4a -6/4a = k |
| (9, -9) | -9 = k(9)a -9= k9a -9/9a = k |
Now that we have k on both the right-hand side of the equations let’s equate the left-hand side expressions. Solve for a from the resulting equation.
-6/4a = -9/9a
-2/4a = -3/9a
-21 / 22a = -31 / 32a
-21 – 2a = -31 – 2a
This equation will only be true when both sides are equal to 1, so the exponents will have to be equal to 0.
1 – 2a = 0
1 = 2a
a = ½
Substitute the value of a back into one of the expressions for k.
k = -6/4a
= -6/ 41/2
= -6/ 2
= -3
Substitute these two values back into the general form of power functions to find the expression for g(x).
g(x) = kxa
= -3x1/2
= -3√x
a. Hence, we have g(x) = -3√x.
Let’s use the two given points to connect the curve. Recall the shape of the square root function’s parent function to know what to expect for the graph of g(x).
b.
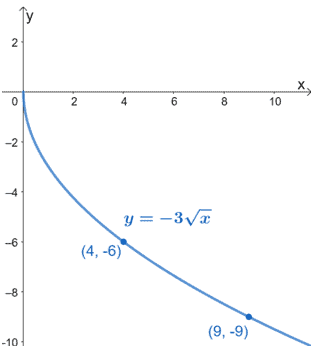
We can find the domain and range of g(x) by inspecting the graph. Since g(x) has a rational exponent with an even denominator, we expect to only have positive values for x. The graph can also confirm this.
Since the graph of g(x) never goes above the negative y-axis, we expect its range to only consist of negative numbers.
c. Hence, the domain of g(x) is [0, ∞) and the range is (-∞, 0]. The graph shows that it is continuously decreasing and the curve is consistently going down.
Example 8
The area of a circle is directly proportional to the square of its radius, r. The area of a circle with a radius of 10 units is 314 units2, and a circle with a radius of 20 units is 1256 units2.
a. Find the power function, A(r), representing the area of a circle in terms of r. What does the coefficient of A(r) represent?
b. Disregarding the restrictions for r, is A(r) odd or even?
c. What is the end behavior of A(r)?
d. If we consider the fact that r represents the circle’s radius, would the domain change?
Solution
Since the area is directly proportional to r2, we can express A(r) as kr2, where k is a nonzero constant.
Let’s use either of the two given pairs of values to find k.
A(r) = kr2
314 = k(10)2
314 = 100k
k = 3.14
a. Substitute k back into the expression, and we have A(r) = 3.14r2. Recall that 3.14 is the approximated value of π, so the coefficient of A(r) represents π.
b. Since A(r) is a quadratic expression; it is an even function.
c. The coefficient of A(r) is positive, and its exponent is even, so we’re expecting the graph to be decreasing when x < 0 and increasing when x > 0. Hence, both ends of the curve are expected to be going up.
d. Originally, since A(r) represents a quadratic expression, we’re expecting it to have a domain (-∞, ∞). But accounting for the fact that measurements must be greater than 0, the domain now becomes (0, ∞).
Practice Questions
![]()
Images/mathematical drawings are created with GeoGebra.
