Vector Calculus – Definition, Summary, and Vector Analysis
Vector calculus opens the door to different types of functions and analyses we can use in different fields. Learning about the core components and the theorems behind vector calculus allows us to describe and study quantities and relationships defined by vector-valued functions.
In vector calculus, we study the differentiation and integration of vector functions. This field is closely related to multivariable calculus.This is why we’re writing this article – to prepared and give you an idea of what to expect and the topics you’ll encounter in vector calculus. In short, our discussion will simply give you a glance at this extensive topic!
What is vector calculus?
Vector calculus is simply the study of a vector field’s differentiation and integration . It’s a core branch in calculus that covers all key concepts to master differentiating and integrating all kinds of
vector functions. In vector calculus, we’ll explore the following:
- Mastering the fundamentals of vector quantities.
- Understanding how vector-valued functions behave in 2D and 3D coordinate systems.
- Evaluate single and even multiple integrals of vector-valued functions.
- Learning how to integrate vector fields (an important technique in higher physics).
We’ll begin our discussion by defining
vectors: these are quantities with both length and direction normally represented by arrows.
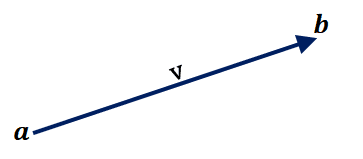
Here’s an example of a vector, $\textbf{v}$, with its tail on $a$ and heads on $b$. This vector can also be displayed as $v$ or $ \overrightarrow{v}$. A vector defined by an ordered triple can be defined by the following:\begin{aligned}<v_1, v_2, v_3> &= v_1\textbf{i} + v_2\textbf{j} + v_3 \textbf{j}\end{aligned}
Summary of Vector Calculus
As we have mentioned, vector calculus and multivariable calculus are closely related. That’s because we’ll learn how to integrate, differentiate, and apply multiple integral operations on vector and multivariable functions at the same time.\begin{aligned}f(x + y) &= 4x^3 – e^y\\ f(t) &= (t^2, 2\ln t)\end{aligned}These are examples of functions that we’ll be dealing with in vector calculus. To give you a better idea on what to expect from this branch of calculus, we’ve summarized some key formulas and concepts you’ll learn in vector calculus:
| Name | Common Notation | Derivative | Integral |
| Curve | \begin{aligned}\textbf{r}(t) \end{aligned} | \begin{aligned}\dfrac{d}{dt} \textbf{r}(t) &=\textbf{r}^{\prime}(t) \end{aligned} | We can apply line integral. |
| Scalar Field | \begin{aligned}f(x)\end{aligned} | \begin{aligned}\text{grad} f &= \overrightarrow{\bigtriangledown} f\end{aligned} | Evaluate integrals using:· Double or triple integral· Surface integrals |
| Parametrized Surface | \begin{aligned}\textbf{D}(x,y) \end{aligned} | \begin{aligned}\textbf{D}_x &=\dfrac{\partial D}{\partial x}\\\textbf{D}_y &=\dfrac{\partial D}{\partial y} \end{aligned} | Evaluate integrals using surface integrals. |
| Vector Field | \begin{aligned}\textbf{F}(\text) \ebf{x}nd{aligned} | Divergence:\begin{aligned}\overrightarrow{\bigtriangledown} \cdot \textbf{F}\end{aligned}Curl:\begin{aligned}\overrightarrow{\bigtriangledown} \times \textbf{F}\end{aligned} | Evaluate integrals using line integrals and surface integrals of vector fields. |
.By the end of our entire topics of vector calculus, you should be able to know these concepts and terms by hear. For now, let’s refresh our knowledge of vector analysis so that we start with vector calculus prepared with our fundamentals!
How to prepare for vector calculus through vector analysis?
Vector analysis covers all the fundamental operations we can perform on scalars and vectors. It’s crucial that we know vector analysis by heart before expanding our knowledge base.In the past, we’ve learned how to perform basic operations on vectors such as: vector
addition,
subtraction, and
scalar multiplication. Here are some examples of how we perform these operations:\begin{aligned}\textbf{u} &= <-3, 2, 1>\\ \textbf{v} &= <4, 6, 8>\\\\ \textbf{u} + \textbf{v} &= <-3 + 4, 2 + 6, 1 + 8>\\&= <1, 8, 9>\\ 2\textbf{v} &= <2 \cdot 4, 2\cdot 6, 2\cdot 8>\\&= <8, 12, 16> \end{aligned}In fact, we’ve also defined the magnitude of vectors as $|\textbf{v}| = \sqrt{v_1^2 + v_2^ + v_3^2}. We’ve also covered
dot and
cross products of vectors as part of our vector analysis tool kit.\begin{aligned}\textbf{u} &= <u_1, u_2, u_3>\\ \textbf{v} &= <v_1, v_2, v_3>\\\\ \textbf{u} \cdot \textbf{v} &= u_1v_1 + u_2v_2 + u_3v3 \\\textbf{u} \times \textbf{v} &= \end{aligned}In fact, through the cross and dot products, we’ve learned how to also relate the two vectors and the
angle formed between them.\begin{aligned}\textbf{u} \cdot \textbf{v} &= |\textbf{u}||\textbf{v}|\cos \theta\\ \cos \theta &= \dfrac{\textbf{u} \cdot \textbf{v}}{|\textbf{u}||\textbf{v}|}\\\\\textbf{u} \times \textbf{v} &= |\textbf{u}||\textbf{v}|\sin\theta\\ \sin\theta &= \dfrac{\textbf{u} \times \textbf{v}}{|\textbf{u}||\textbf{v}|}\end{aligned}We’ve also defined normal and orthogonal vectors in the past and knowing these properties will be a great help when simplifying vectors.
| Orthogonal Vectors | Normal Vectors |
| \begin{aligned}\textbf{u} \cdot \textbf{v} &= 0\end{aligned} | \begin{aligned}\textbf{u} \times \textbf{v} &= |\textbf{u}||\textbf{v}|\end{aligned} |
To learn more about other vector analysis terms, theorems, and formulas, head over to our section for
vectors. Knowing these concepts before going through more complex topics in vector calculus will make a lot of difference! For now, let’s some more vector analysis problems to refresh our current knowledge as well.
Example 1Given that $\textbf{u} = 4\textbf{i} – 2\textbf{j} + 3\textbf{k}$ and $\textbf{u} = 2\textbf{i} + 3\textbf{j} – \textbf{k}$, calculate the following:a. $4\textbf{u} – 3\textbf{v}$
b. $\textbf{u} \cdot \textbf{v}$
c. $\textbf{u} \times \textbf{v}$
SolutionTo find $4\textbf{u} – 3\textbf{v}$, simply distribute the scalar factors to $\textbf{u}$ and $\textbf{v}$ then subtract the result.\begin{aligned}4\textbf{u} &= 16\textbf{i} – 8\textbf{j} + 12\textbf{k} \\3\textbf{v} &= 4\textbf{i} + 6\textbf{j} – 2\textbf{k}\\\\ 4\textbf{u} – 3\textbf{v}&= (16 – 4)\textbf{i} + (-8- 6)\textbf{j} + (12 – -2)\textbf{k}\\&= 12\textbf{i} – 14\textbf{j} + 14\textbf{k}\end{aligned}Apply the appropriate formulas to find the two vectors’ dot and cross products.\begin{aligned}\textbf{u} &= <u_1, u_2, u_3>\\ \textbf{v} &= <v_1, v_2, v_3>\\\\ \textbf{u} \cdot \textbf{v} &= u_1v_1 + u_2v_2 + u_3v3 \\\textbf{u} \times \textbf{v} &= \end{aligned}Hence, we have the following:
| \begin{aligned}\textbf{u} \cdot \textbf{v} \end{aligned} | \begin{aligned}\textbf{u} \cdot \textbf{v} &= 4(2) + (-2)(3) + 3(-1)\\&= 8 – 6 -3\\&=1\end{aligned} |
| \begin{aligned}\textbf{u} \times \textbf{v} \end{aligned} | \begin{aligned}\textbf{u} \times \textbf{v} &= (-2\cdot -1 – 3\cdot 3)\textbf{i} + (3\cdot 2 – 4\cdot -1)\textbf{j} + (4\cdot 3- -2\cdot 2)\textbf{k}\\&= (-7)\textbf{i} + (10)\textbf{j} + (16)\textbf{k} \\&=-7\textbf{i} + 10\textbf{j} + 16\textbf{k} \end{aligned} |
Example 2What is the angle between $\textbf{u} = <2, 3, -1>$ and $\textbf{u} = <1, 2, 1>$?
SolutionFirst, calculate their magnitudes as shown below:\begin{aligned}|\textbf{u}| &= \sqrt{2^2 + 3^2 + (-1)^2}\\&= \sqrt{14}\\|\textbf{v}| &= \sqrt{1^2 + 2^2 + 1^2}\\&= \sqrt{6}\end{aligned}Now, take the dot product of the two vectors first. Hence, we have\begin{aligned}\textbf{u} \cdot \textbf{v} &= 2(1) + (3)(2) + -1(1)\\&= 2 + 6 -1\\&= 7\end{aligned}Use the fact that $\cos \theta = \dfrac{\textbf{u} \cdot \textbf{v}}{|\textbf{u}||\textbf{v}|}$.\begin{aligned}\cos \theta &= \dfrac{7}{ \sqrt{14} \cdot sqrt{6}}\\ \theta &= \cos^{-1} \left(\dfrac{7}{\sqrt{84}}\right) &\approx 40.20^{\circ}\end{aligned}This means that the angle formed between $\textbf{u} = <2, 3, -1>$ and $\textbf{u} = <1, 2, 1>$ is equal to $40.20^{\circ}$.
Practice Questions
1. Given that $\textbf{u} = 6\textbf{i} – \textbf{j} + 4\textbf{k}$ and $\textbf{u} = 2\textbf{i} + \textbf{j} -2 \textbf{k}$, calculate the following:
a. $2\textbf{u} – 5\textbf{v}$
b. $\textbf{u} \cdot \textbf{v}$
c. $\textbf{u} \times \textbf{v}$
2. What is the angle between $\textbf{u} = <-2, 4, -2>$ and $\textbf{u} = <3, 1, 2>$?
Answer Key
1.
a. $2\textbf{u} – 5\textbf{v} =2\textbf{i} – 7\textbf{j} + 18\textbf{k} $
b. $\textbf{u} \cdot \textbf{v} = 3$
c. $\textbf{u} \times \textbf{v} =-2\textbf{i} + 20\textbf{j} + 8\textbf{k} $
2. $\theta \approx 109.11^{\circ}$
