Change of Base – Formula, Explanation, and Example

Notice how most calculators have $\log$ and $\ln$ on their keys but rarely a logarithmic key for different bases? This is why learning how to change bases is important if we need to find the exact values of different logarithmic expressions.

The change of base formula helps us manipulate logarithmic expressions by rewriting them in bases of 10 or e. This formula involves finding the ratios between the logarithms between the original argument and base.

We’ve learned about logarithms in the past, so make sure to review these concepts before diving right into changing bases of logarithmic expressions.

• Understanding the definition of logarithms.
• Refreshing the difference between regular and natural logarithms.
• Recall the different properties and rules of logarithms.

Let’s go ahead and further our knowledge of logarithms by learning how to rewrite logarithmic expressions to have bases that are easier to evaluate and manipulate.  We’ll also learn how to apply this to estimate the values of unknown variables regardless of the logarithmic expressions’ bases.

We can start by first understanding what the change of property represents.

What is the change of base formula?                

The change of base formula allows us to rewrite a logarithmic expression so that the new expression contains a different base. We normally use this whenever we need to evaluate logarithmic values on calculators that make use of either $\log$ (for the base of $10$) or $\ln$ (for the base of $e$).

Let’s say that $a$, $b$, and $x$ are positive and $a \neq 1$ as well as $b \neq 1$.

The formula above shows how we can rewrite a logarithmic expression with base $a$ as a ratio of two expressions with a base of $b$. This shows how flexible this formula is to accommodate all kinds of bases.

Curious about how we have this helpful formula? Why don’t we refresh our knowledge on logarithmic properties to prove this formula?

Proof of the change of base formula

Let’s say we have  $y = \log_a x$, this means that $a^y = x$. We can then perform the following:

• Take the $\log_b$ of both sides of the equation.
• Apply the power rule of logarithms, $\log_a M^n = n \log_a M$.
• Isolate $y$ on the left-hand side of the equation.
• Replace $y$ with $\log_a x$.

$ \begin{aligned}a^y &= x\\\log_b a^y &= \log_b x\\y\log_b a &= \log_b x\\y &= \dfrac{\log_b x}{\log_b a}\\\log_ax &= \dfrac{\log_b x}{\log_b a}\end{aligned}$

Hence, we’ve just proved the change of base formula using the previous properties we’ve learned in the past. Do your best to understand and recreate this proof of your own, as it’s going to help you review important properties and remember the formula faster.

How to change the base of a log?                

Now that we’ve learned about the change of base formula, $\log_ax = \dfrac{\log_b x}{\log_b a}$, let’s learn how we can apply them to change the base of a logarithmic expression.

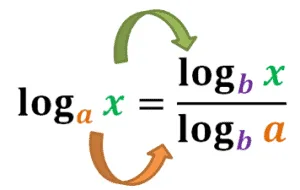
When rewriting $\log_a x$ so that it is now in terms of base $b$, we can apply the following steps:

Step 1: Expect a ratio with two logarithmic expressions in terms of base $b$.

Step 2: In the numerator, write the logarithm of $x$ with base $b$.

Step 3: In the denominator, find the old base’s logarithm in terms of base $b$.

Step 4: Simplify whenever possible or evaluate the ratio using a calculator.

When finding the exact values of logarithms, we normally use $b = 10$ or $b = e$ since $\log_{10} = \log$ and $\log_e = \ln$ are available on all scientific calculators.

Why don’t we go ahead and use this formula to change $\log_8 56$ in terms of i) base of $10$ and ii) base of $e$?  Let’s also use a calculator to estimate each of the two values.

This goes to show that we can either use $\log$ or $\ln$ (and of course, the change of base formula) on the calculator to find the exact values of logarithmic expressions with different base values.

We can also rewrite expressions so that they have bases that are easier to manipulate or evaluate.

Sounds easy, right? Let’s go ahead and try out more problems that involve the change of base formula and see how we can apply it extensively.

Example 1

Use the change of base formula, then use a calculator to evaluate the following expressions—approximate your answer to the nearest thousandths.
a. $\log_4 5$
b. $\log_2 12$
c. $\log_6 40$
d. $\log_9 12$

Solution

Most calculators only contain $\log$ or $\ln$ keys, so it will best if we change each expression in terms of either base $10$ or base $e$. We’ll show the working out for each of the bases so that you can compare them with your solution.

First, let’s recall the change of base formula: $\log_a x = \dfrac{\log_b x}{\log_b a}$, where we rewrite $\log_a x$ in terms of the new base, $b$.

For $\log_4 5$, for example, we’ll find the ratio of $\log 5$ and $\log 4$ or $\ln 5$ over $\ln 4$. We’ll apply similar processes for the rest, and the table below summarizes those calculations.

As you can see from the calculations, we’ll get the same results when we use either $\log$ or $\ln$. This should show you that it’s okay to use either of the two bases to estimate the value of a given expression.

Hence, we have the following values to the nearest thousandths:
a. $\log_4 5 = 1.161$
b. $\log_2 12 = 3.585$
c. $\log_6 40 = 2.059$
d. $\log_9 12 = 1.131$
Make sure to review your own work and see if you have these four values.

Example 2

Find the exact values of the following expressions without using the calculator.

a. $\log_{4} 32$
b. $\log_{0.1} 1000$
c. $\log_{\frac{1}{27}} 243$

Solution

There are instances where we’ll need to use the change of base formula to find the exact values. This is normally used when the base and the argument can be expressed as a power of a smaller common factor.

For example, in $\log_{4} 32$, we can express $4$ and $32$ as powers of $2$, so it makes sense to rewrite $\log_{4} 32$ so that it has a base of $2$ instead. Through the change of base formula, $\log_a x = \dfrac{\log_b x}{\log_b a}$, we have the new expression shown below.

$\begin{aligned}\log_{\color{red} 4 } {\color{blue}32} &= \dfrac{\log_{\color{green} 32} \color{blue}12}{\log_{\color{green} 2} \color{red} 4}\end{aligned}$

Since $4 = 2^2$ and $32 = 2^5$, we can rewrite the numerator and denominator then further simplify the expression using the property, $\log_b b^a = a$.

$\begin{aligned}\dfrac{\log_2 32}{\log_2 4} &= \dfrac{\log_2 2^5}{\log_2 2^2}\\&= \dfrac{5}{4}\end{aligned}$

We’ll apply a similar process for $\log_{0.1} 1000$, but this time, we’ll express $0.1$ and $1000$ as powers of $10$. Note that $0.1 = 10^{-1}$ and $1000 = 10^3$, so we have the following:

$\begin{aligned}\log_{\color{red} 0.1 } {\color{blue}1000} &= \dfrac{\log_{\color{green} 10} \color{blue}1000}{\log_{\color{green} 10} \color{red} 0.1}\\&= \dfrac{\log_{10} 10^3}{\log_{10} 10^{-1}} \\&= \dfrac{3}{-1} \\&= -3\end{aligned}$

For the third item, we can express $\dfrac{1}{27}$ as $3^{-3}$ and $243$ as $3^5$. It will be ideal if we rewrite $\log_{\frac{1}{27}} 243$ so that it has a base of $3$.

$\begin{aligned}\log_{\color{red} \frac{1}{27} } {\color{blue}243} &= \dfrac{\log_{\color{green} 3} \color{blue}343}{\log_{\color{green} 3} \color{red} \dfrac{1}{27}}\\&= \dfrac{\log_{3} 3^5}{\log_{3} 3^{-3}} \\&= \dfrac{5}{-3} \\&= -\dfrac{5}{3}\end{aligned}$

Hence, we’ve shown how it’s also possible to find the exact values by rewriting logarithmic expressions and by smartly changing their bases. Summarizing the calculations shown, we have the following results:

a. $\log_{4} 32 = \dfrac{5}{4}$
b. $\log_{0.1} 1000 = -3$
c. $\log_{\frac{1}{27}} 243 = -\dfrac{5}{3}$

Example 3

If $4^x = 72$, what is the value of $x$ to the nearest thousandths?

Solution

To find the value of $x$, let’s go ahead and take $\log_4$ on both sides of the equation.

$\begin{aligned} 4^x &= 72\\ \log_4 4^x &= \log_4 72\end{aligned}$

Recall that $\log_a a^x = x$, so we can isolate $x$ on the left side of the equation. To find the exact value of $x$, to the nearest thousandths, use the change of base formula to the nearest thousandths.

We can either change the bases to $10$ or $e$ so that we can use $\log$ or $\ln$ on the calculator.

$ \begin{aligned} x &= \log_4 72 \\ &= \dfrac{\log_{\color{green} 10} \color{blue}72}{\log_{\color{green} 4} \color{red} 4}\\&= \dfrac{\log 72}{\log 4}\\&\approx 3.085\end{aligned}$

We can also verify this solution by checking the value of $4^{3.085}$ equal to $72.0037$.This means that $x$ is approximately equal to $3.085$.

Example 4

Show that $\log_{27} 1000 = \log_3 10$ using logarithmic properties.

Solution

To show that both sides of the equation are equal, it will be best if we rewrite either side so that they share the same bases.

It’s much easier to rewrite $\log_{27} 1000$ in terms of base $3$ since $27$ is also equal to $3^3$.

 $\begin{aligned}\log_{\color{red} 27 } {\color{blue}1000} &= \dfrac{\log_{\color{green} 3} \color{blue}1000}{\log_{\color{green} 3} \color{red} 27}\\&= \dfrac{\log_3 1000}{\log_3 3^3}\end{aligned}$

We can rewrite the denominator using $\log_a a^x = x$ to simplify the expression further.

$\begin{aligned}\dfrac{\log_3 1000}{\log_3 3^3} &= \dfrac{\log_3 1000}{3}\\&= \dfrac{1}{3} \log_3 1000 \end{aligned}$

Rewrite $1000$ as $10^3$ and use the power property that $\log_a M^n = n \log_a M$ to further rewrite the expression.

$\begin{aligned}\dfrac{1}{3} \log_3 1000 &= \dfrac{1}{3} \log_3 10^3\\&= \dfrac{1}{3}\cdot3 \log_3 10\\&=\log_3 10 \end{aligned}$

Hence, we’ve shown that $\log_{27} 1000 = \log_3 10$ by using the different logarithmic properties.

Example 5

Given that $2^x = 6^{-2x + 5}$, estimate the value of $x$ to the nearest hundredths.

Solution

To remove the variables on the exponents, we can either take $\log_2$ or $\log_6$ on both sides of the equation. We’ll show you how it’s going to be when we take $\log_2$ of both sides of the equation.

$\begin{aligned}2^x &= 6^{-2x + 5}\\ \log_2 2^x &= \log_2 6^{-2x + 5}\end{aligned}$

Simplify the left-hand side of the equation using the fact that $\log_a a^x = x$. Then use the power rule,  $\log_a M^n = n \log_a M$, to simplify the equation’s right-hand side.

$\begin{aligned}x &= \log_2 6^{-2x + 5}\\x&= (-2x + 5) \log_2 6\end{aligned}$

Expand the equation’s right-hand side by distributing $\log_2 6$ to each of the terms inside the parenthesis.

$\begin{aligned}x&= -2(\log_2 6)x + 5(\log_2 6)\\ x + 2\log_2 6 x&= 5\log_2 6  \end{aligned}$

We can then factor out $x$ on the left-hand side then isolate $x$ to find its exact value.

$\begin{aligned}x(1 + 2\log_2 6) &= 5\log_2 6\\x&= \dfrac{5 \log_2 6}{1 + 2\log_2 6} \end{aligned}$

To estimate the value of $x$ using a calculator, we can change the base of $\log_2 6$ so that we can use either $\log$ or $\ln$. The solution below makes use of $\ln$, so we’re rewriting $\log_2 6$ in terms of base $e$.

$\begin{aligned}\log_{\color{red} 2 } {\color{blue}6} &= \dfrac{\log_{\color{green} e} \color{blue}6}{\log_{\color{green} e} \color{red} 2}\\&= \dfrac{\ln 6}{\ln 2}\end{aligned}$

Let’s replace $\log_2 6$ with $\dfrac{\ln 6}{\ln 2}$ in the expression for $x$. Then use a calculator to estimate the value of $x$ to the nearest thousandths.

$\begin{aligned}x&= \dfrac{5 \cdot \dfrac{\ln 6}{\ln 2}}{1 + 2\cdot \dfrac{\ln 6}{\ln 2}} \\&\approx2.095\end{aligned}$

We can also double-check if this value of $x$ is correct by substituting $x = 2.095$ into the original equation and see if both sides’ values are close enough to each other.

$\begin{aligned}2^{2.095} &= 6^{-2(2.095) + 5}\\4.272 &\approx 4.268\end{aligned}$

 This means that the value of $x$ can be estimated to be equal to $2.095$.