- Home
- >
- Reciprocal Function – Properties, Graph, and Examples
JUMP TO TOPIC
Reciprocal Function – Properties, Graph, and Examples
 Finding the reciprocal function will return a new function – the reciprocal function. These functions exhibit interesting properties and unique graphs. When two expressions are inversely proportional, we also model these behaviors using reciprocal functions.
Finding the reciprocal function will return a new function – the reciprocal function. These functions exhibit interesting properties and unique graphs. When two expressions are inversely proportional, we also model these behaviors using reciprocal functions.
Reciprocal functions consist of two components: a constant on the numerator and an algebraic expression in the denominator.
From its definition to its graph, we’ll learn extensively about reciprocal functions in this article. We’ll learn the following:
- Understanding the properties of reciprocal functions.
- Graphing reciprocal functions using different methods.
- Determining the function’s expression based on its graph.
We use reciprocal functions when describing relationships inversely proportional to each other such as the stress and elasticity of an object, time and speed’s relationship, and more. This is why learning about reciprocal functions can help us in our current and future advanced math classes.
So, why don’t we go ahead and begin with its form and definition?
What is a reciprocal function?
The common form of reciprocal functions that we may encounter is $y = \dfrac{k}{x}$, where $k$ is a real number. This means that reciprocal functions are functions that contain constant on the numerator and algebraic expression in the denominator. Here are some examples of reciprocal functions:
- $f(x) = \dfrac{2}{x^2}$
- $g(x) = \dfrac{1}{x + 1} – 4$
- $h(x) = -\dfrac{2}{x + 4} + 3$
As we can see from the three examples, all functions have numerator constants and denominators containing polynomials.
The general form of reciprocal functions is $\mathbf{y}$ $\mathbf{= \dfrac{x}{(x – h)} + k}$, where $a$, $h$, and $k$ are real number constants.
How to find the reciprocal of a function?
As we have learned in the past, we can determine a number’s reciprocal by dividing 1 by the given number. The same concept applies when we find a function’s reciprocal function – we divide 1 by the function’s expression.
Here’s a table to compare the reciprocal that we learned in the past and reciprocal functions:
| Reciprocal | Reciprocal Function |
| Given a number, $k$, its reciprocal is $\dfrac{1}{k}$. | Given a function, $f(x)$, its reciprocal function is $\dfrac{1}{f(x)}$. |
| The product of $k$ and its reciprocal is equal to $k$ · $\dfrac{1}{k} = 1$. | The product of $f(x)$ and its reciprocal is equal to $f(x)$ · $\dfrac{1}{f(x)} = 1$. |
| Given $\dfrac{1}{k}$, its value is undefined when $k = 0$. | Given $\dfrac{1}{f(x)}$, its value is undefined when $f(x) = 0$. |
The table shows that reciprocals and reciprocal functions share similar characteristics and properties. Let’s go ahead and observe the function $y = 2x – 1$.
- This means that if we want to find the reciprocal of $y = 2x – 1$, its reciprocal can be expressed as $y = \dfrac{1}{2x – 1}$.
- We can also confirm the product of $2x – 1$ and its reciprocal:
$(2x – 1) \cdot \dfrac{1}{2x – 1} = 1$
- This also means that $2x – 1$ must never be zero, so $x$ must never be $\frac{1}{2}$.
How to graph reciprocal functions?
There are different ways for us to graph reciprocal functions. In this article, we’ll focus on two methods:
- Graphing reciprocal functions by finding the function’s table of values first.
- Graphing reciprocal functions using different transformation techniques.
How to graph functions using their tables of values
Let’s go ahead and start with graphing the parent function, $y = \frac{1}{x}$ by first finding its table of values.
- Find the value of the function at different values of $x$.
- Plot these points on the $xy$-coordinate system.
- Graph the curves using these points.
| $\mathbf{x}$ | $-3$ | $-2$ | $-1$ | $-\frac{1}{2}$ | $-\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | $1$ | $2$ | $3$ |
| $\mathbf{y}$ | $-\frac{1}{3}$ | $-\frac{1}{2}$ | $-1$ | $-2$ | $-3$ | $3$ | $2$ | $1$ | $\frac{1}{2}$ | $\frac{1}{3}$ |
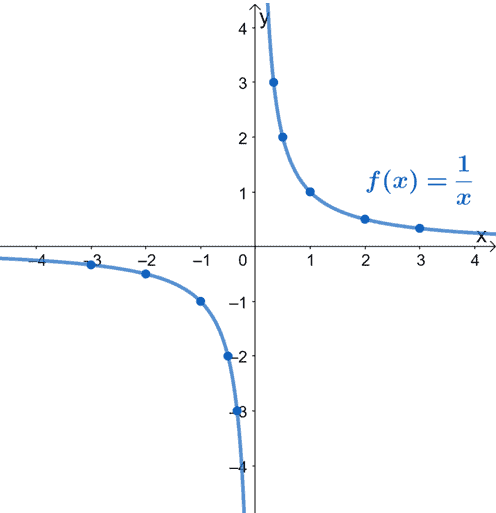
As we have expected, $\dfrac{1}{x}$ can never be equal to $0$, and $x$ can never be zero. From the graph, we can see other than the restrictions, and the function $y = x$ can be any real number. Why don’t we summarize its domain and range?
| Domain | $(-\infty, 0) \cup (0, \infty)$ |
| Range | $(-\infty, 0) \cup (0, \infty)$ |
Since we have restrictions at $x = 0$ and $y = 0$, these equations also represent the vertical and horizontal asymptotes of $f(x) = \frac{1}{x}$. Let’s include these asymptotes on our final graph:
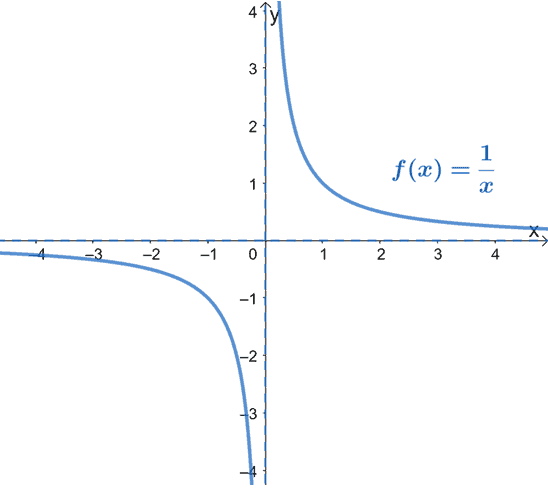
We can also use the graph of $y = \dfrac{1}{x}$ to graph other reciprocal functions. We can do this by applying different transformation techniques.
How to graph reciprocal functions by transformation
Here are some common graph transformations that we’ve already learned in the past:
- Vertically and horizontally translating functions.
- Vertically and horizontally stretching functions.
- Shrinking functions vertically and horizontally.
These techniques can be applied as well on the graph of $y = \dfrac{1}{x}$ so that we can graph different reciprocal functions. Let’s try graphing $y = \dfrac{2}{x – 1} + 4$ by first identifying the transformations done on $y = \dfrac{1}{x}$ to attain our given function.
$y = \mathbf{2} \left(\frac{1}{x-\mathbf{1}}\right) \mathbf{+4}$
From this, we can see that we’ll need to perform the following transformations on the graph of $y = \dfrac{1}{x}$:
- Translate the graph one unit to the right.
- Stretch the graph vertically by two units.
- Translate the graph four units upward.
Let’s start by moving the graph of $y = \frac{1}{x}$ one unit to the right. Use reference points to guide you. The $x$-coordinates must be one unit greater.
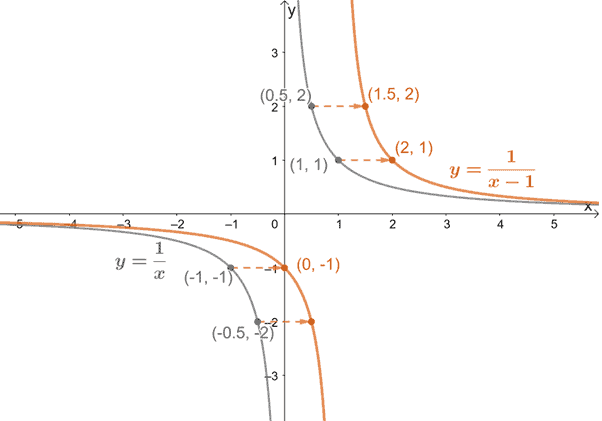
Now, stretch the graph vertically by two units. Check our resulting graph by making sure that the $y$-coordinate’s values are doubled.
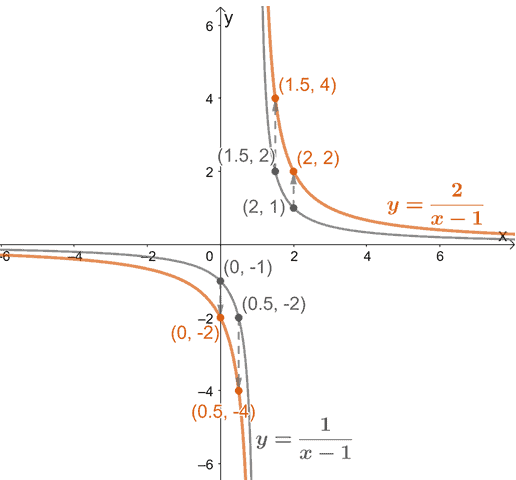
Move the resulting graph four units upward. Double-check your resulting graphs by making sure our reference points’ $y$-coordinates have increased by $4$.
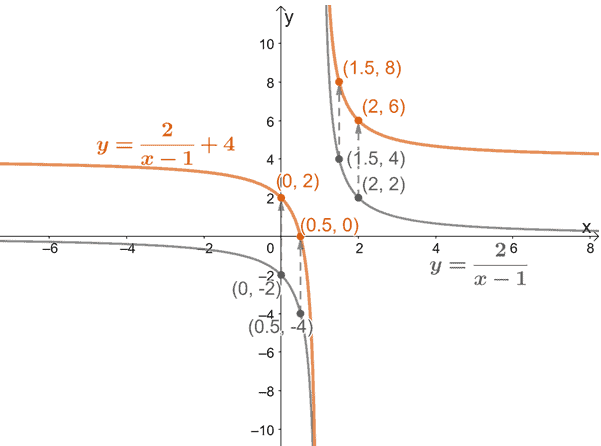
Hence, we’ve shown that we can graph reciprocal functions using transformations.
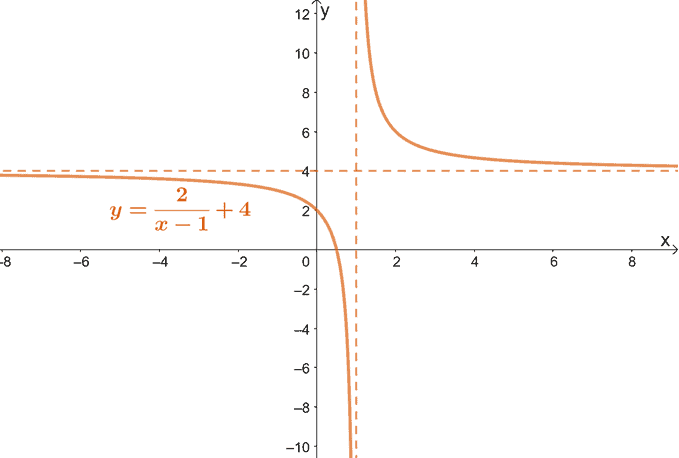
Notice that the asymptotes have shifted too? This makes sense since our new asymptotes can be calculated as shown below:
| Vertical Asymptote | Horizontal Asymptote |
The expression $\frac{2}{x-1}$ can’t be $0$, so $y \neq 4$. Asymptote:$ y = 4$ | The denominator $x – 1$ can’t be $0$, so $x \neq 1$. Asymptote: $x = 1$ |
Using the general form of reciprocal functions, the vertical asymptote can be expressed as y = k, and the horizontal asymptote can be expressed as x = h.
From the graph and the asymptotes, we can also find the function’s domain and range:
| Domain | $(-\infty, 1) \cup (1, \infty)$ |
| Range | $(-\infty, 4) \cup (4, \infty)$ |
Here’s a quick exercise for you:
- Try graphing $y = -\dfrac{1}{x}$ on your own and compare this with the graph of $y = \dfrac{1}{x}$.
- Sketch $y = x$ and $y = -x$ on the graphs of $y = \dfrac{1}{x}$ and $-\dfrac{1}{x}$.
- What can you say about each pair of graphs?
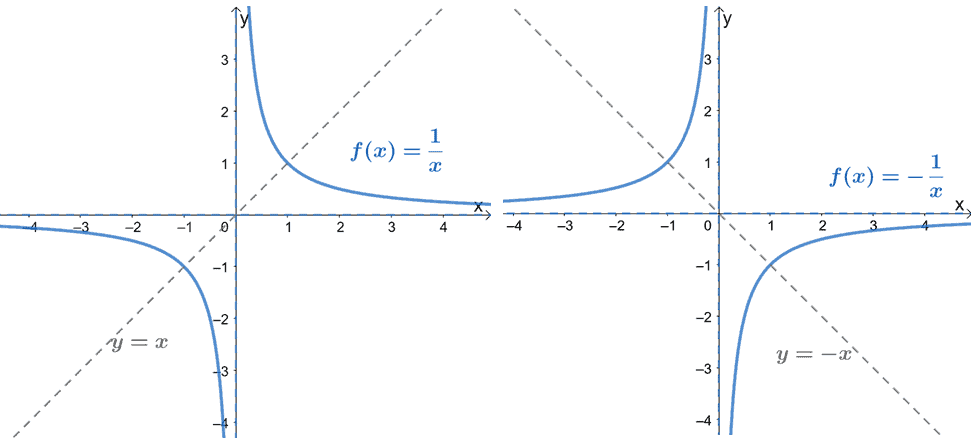
Observe that when the function is positive, it is symmetric with respect to the equation $\mathbf{y = x}$. Meanwhile, when the function is negative (i.e., has a negative constant), it is symmetric with respect to the equation $\mathbf{y = -x}$.
Summary of reciprocal function definition and properties
Before we try out some more problems that involve reciprocal functions, let’s summarize everything that we have learned so far about these unique functions.
- Reciprocal functions are functions that have a constant on their denominator and a polynomial on their denominator.
- The reciprocal of a function, $f(x)$, can be determined by finding the expression for $\dfrac{1}{f(x)}$.
- We can graph a reciprocal function using the function’s table of values and transforming the graph of $y = \dfrac{1}{x}$.
- Make sure to find the vertical and horizontal asymptotes of the function.
- The domain and range of a reciprocal function will depend on the asymptotes’ values.
- The symmetry of the reciprocal function’s graph will depend on the constant’s sign.
Example 1
If $g(x)$ is the reciprocal of $f(x)$, what is the value of $g(x) \cdot f(x)$?
Solution
Find the expression for $g(x)$ in terms of $f(x)$. Since it is the reciprocal of $f(x)$, we have $g(x) = \frac{1}{f(x)}$.
Multiply the two expressions to find their product.
$\begin{aligned} g(x) \cdot f(x)&= \frac{1}{f(x)}\cdot f(x)\\&=\mathbf{1}\end{aligned}$
We can also use the fact that a function’s product and its reciprocal will always be equal to 1.
Example 2
What are the reciprocals of the following functions?
a. $f(x) = x^2 – 4$
b. $g(x) = \dfrac{x}{2}$
c. $h(x) = \dfrac{3(x – 1)}{5}$
Solution
To find the reciprocal of a function, we can divide 1 by the expression.
a. For $f(x) = x^2 – 4$, we simply divide $1$ by the $f(x)$’s expression, hence its reciprocal is equivalent to $\mathbf{\dfrac{1}{x^2-4}}$.
b. When finding the reciprocal of a rational expression, we switch the numerator and denominator positions. This means that its reciprocal is $\mathbf{\dfrac{2}{x}}$.
We apply the same process when finding the reciprocal of $h(x)$. Hence, $\frac{1}{h(x)}\mathbf{=\dfrac{5}{3(x-1)}}$.
Example 3
Complete the table below by finding the reciprocal functions’ symmetry, domain, range, vertical asymptote, and horizontal asymptote.
| Function | Symmetry | Vertical Asymptote | Horizontal Asymptote | Domain | Range |
| $y=-\dfrac{3}{x}$ | |||||
| $y=\dfrac{2}{2x+1}$ | |||||
| $y=\dfrac{4}{x-4}+2$ | |||||
| $y=-\dfrac{3}{x-2}+5$ |
Solution
When finding the symmetry of the reciprocal function, we base it on the constant’s sign.
- If the constant is negative, its graph is symmetric with respect to the line $y = -x$.
- If the constant is positive, the graph is symmetric with respect to $y = x$.
Inspect the equation’s expression and compare it with the general form, $\dfrac{a}{x-h} + k$.
- The vertical asymptote will be $x = h$.
- The horizontal asymptote will be $y = k$.
The domain for each expression will be $(-\infty,h)\cup(h, \infty)$ and the range will b e$(-\infty,k)\cup(k, \infty)$.
Let’s use all the information to fill in the table:
| Function | Symmetry | Vertical Asymptote | Horizontal Asymptote | Domain | Range |
| $y=-\dfrac{3}{x}$ | $y = -x$ | $x = 0$ | $y = 0$ | $(-\infty,0)\cup(0, \infty)$ | $(-\infty,0)\cup(0, \infty)$ |
| $y=\dfrac{2}{2x+1}$ | $y = x$ | $x = 0$ | $y = 1$ | $(-\infty,0)\cup(0, \infty)$ | $(-\infty,0)\cup(0, \infty)$ |
| $y=\dfrac{4}{x-4}+2$ | $y = x$ | $x = 4$ | $y = 2$ | $(-\infty,4)\cup(4, \infty)$ | $(-\infty,2)\cup(2, \infty)$ |
| $y=-\dfrac{3}{x-2}+5$ | $y = -x$ | $x = 2$ | $y = 5$ | $(-\infty,2)\cup(2, \infty)$ | $(-\infty,5)\cup(5, \infty)$ |
Example 4
Choose from the four functions given in Example 3 and graph the two of them:
- One function is to be graphed by finding the table of values.
- The second function is to be graphed by transforming $y=\dfrac{1}{x}$.
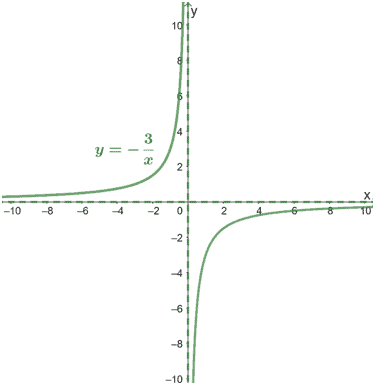
Let’s graph the first function, $y=-\dfrac{3}{x}$ by finding its table of values to graph the first half of its curve.
| $\mathbf{x}$ | $\mathbf{y = -\dfrac{3}{x}}$ |
| $\dfrac{1}{3}$ | $-9$ |
| $\dfrac{1}{2}$ | $-6$ |
| $1$ | $-3$ |
| $3$ | $-1$ |
Reflect the curve over its line of symmetry to graph the remaining half of the curve.
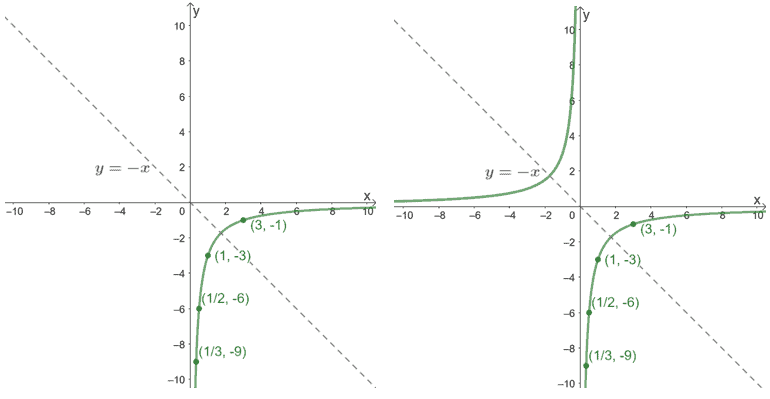
Include the vertical and horizontal asymptotes in your final graph.
Let’s try to graph the third function from Example 3: $y = \dfrac{4}{x-4} + 2$. We can start by identifying the transformations we need to perform on $y = \dfrac{1}{x}$.
$\frac{4}{x-4}+2=\mathbf{4}\left(\dfrac{1}{x\mathbf{-4}}\right)\mathbf{+2}$
Hence, we have the following transformations:
- Translate $y = \dfrac{1}{x}$ to the right by $4$ units.
- Vertically stretch the function’s graph by $4$.
- Translate the resulting function by $2$ units upwards.
Let’s perform the following transformations in order to graph $y = \dfrac{4}{x-4} + 2$.
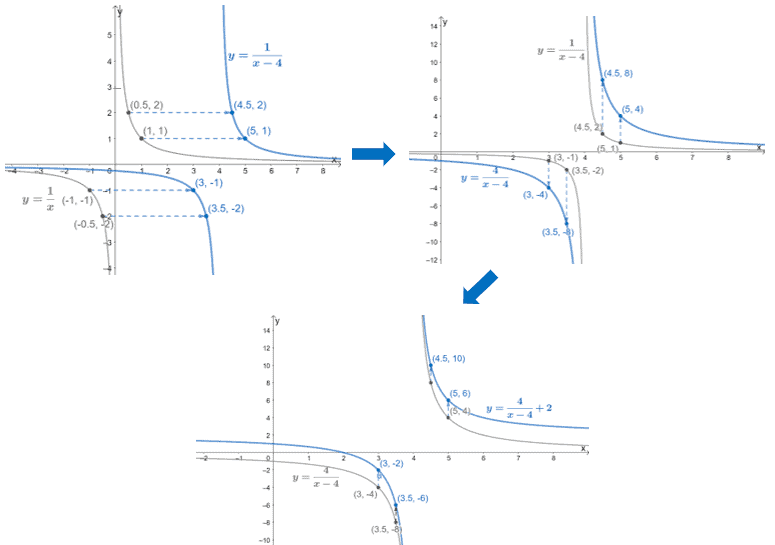
Include the vertical and horizontal asymptotes of the function as well in its final graph.
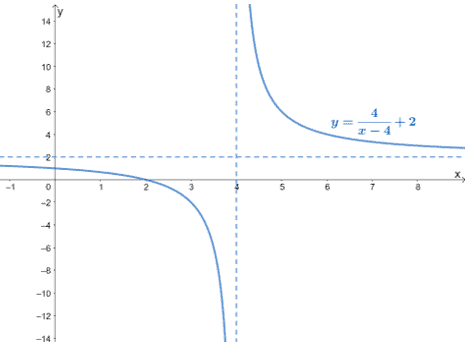
The graph confirms that our domain and range from Example 3 is consistent for this function:
| Domain | $(-\infty,4)\cup(4, \infty)$ |
| Range | $(-\infty,2)\cup(2, \infty)$ |
This problem shows that there are advantages in using both methods when graphing reciprocal functions.
Practice Questions
![]()
Images/mathematical drawings are created with GeoGebra.
