Types of Angles – Explanation & Examples

Different types of angles exist in nature, and each one of them carries much importance in our daily lives.

For example, architects and engineers use angles when designing machines, buildings, roads, and bridges.

In sports, athletes use angles to enhance their performance. For example, a person must spin with the disk at a certain angle to throw it far in short put. In soccer, you must use a certain angle to pass the ball to the next player.

Carpenters and artisans also use angles to fabricate objects such as sofas, tables, chairs, pails, etc. Artists use angles to sketch portraits and paintings. Fashion designers also use angles to come with certain with the best outfits. For these reasons, it is, therefore, necessary we learn the different types of angles.

(To go through the basic explanation of angles, you can consult the previous article, “Angles.”)

Different Types of Angles

Angles are classified based on:

Magnitude
Rotation

Classification of angles based on their magnitude

There are seven types of angles based on their degree measurement. They include:

Zero Angles
Acute Angles
Right Angles
Obtuse Angles
Straight Angles
Reflex Angles
Complete Angle

– Zero Angle

A zero angle (0°) is an angle formed when both the angle’s arms are at the same position.

Illustration:

∠ RPQ = 0° (zero angle)

– Acute Angle

An acute angle is an angle that is more than 0° but less than 90°. Common examples of acute angles include: 15°, 30°, 45°, 60°, etc.

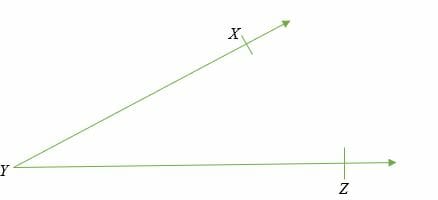
∠ XYZ is greater than 0° but less than 90° (acute angle)

– 90 Degree Angle

A 90-degree angle, also known as a right angle, is an angle whose measure is equal to 90° is called a right angle. Right angles are represented by drawing a small square box between the arms of an angle.

Illustration:

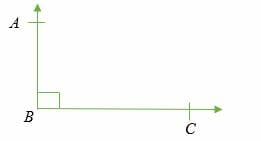
∠ ABC = 90° (right angle)

There will be a whole article on right triangles in the next section (of Triangles).

– Obtuse Angle

An obtuse angle is a type of angle whose degree measurement is more than 90° but less than 180°. Examples of obtuse angles are: 100°, 120°, 140°, 160°, 170°, etc.

∠ PQR is an obtuse angle because it’s less than 180° and greater than 90°.

– Straight Angle

As the name suggests, a straight angle is an angle whose measure is equal to 180° (straight line)

Illustration:

∠ XYZ =180° (straight angle)

– Reflex Angle

Reflex angles are the types of angles whose degree measurement is more than 180° but less than 360°. Common examples of reflex angles are; 200°, 220°, 250°, 300°, 350°, etc.

Illustration:

∠ PQR is greater than 180° but less than 360°

– Complete Angle

A complete angle is equal to 360°. 1 revolution is equal to 360°.

Illustration:

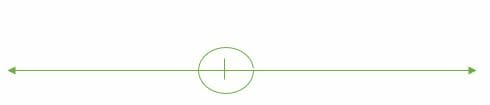
Classification of angles on the basis of rotation

Based on the direction of rotation, angles can be classified into two categories, namely;

Positive Angles
Negative Angles

Positive Angles

Positive angles are the types of angles whose measurements are taken in a counterclockwise direction from the base.

Negative Angles

Negative angles are measured in a clockwise direction from the base.

Other types of angles

Apart from the above discussed angles, there are other types of angles known as pair angles. They are called pair angles because they appear in pairs to show a certain property. These are:

Adjacent angles have the same vertex and arm.
Complementary angles: Pair angles that add up to 90º.
Supplementary angles: Pair angles whose sum of angles is equal to 180º.
Vertically Opposite Angles. Vertically opposite angles are equal.
Alternate Interior Angles: Alternate interior angles are pair angles formed when a line intersects two parallel lines. Alternate interior angles are always equal to each other.
Alternate Exterior Angles: Alternate exterior angles are simply vertical angles of the alternate interior angles. Alternate exterior angles are equivalent.
Corresponding Angles: Corresponding angles are pair angles formed when a line intersects a pair of parallel lines. Corresponding angles are also equal to each other.

We saw a brief overview of the different types of angles. Next, we will see the detailed articles on the most common types of angles (Complementary Angles, Supplementary Angles, etc.).