Acute Angle – Explanation and Examples

An acute angle is an angle larger than a zero angle and smaller than a right angle.

In degrees, an acute angle measures greater than $0$ degrees and less than $90$ degrees. In radians, an acute angle is one with a measure greater than $0$ radians and less than $\frac{\pi}{2}$ radians.

Acute angles are used mathematically in geometry, trigonometry, and calculus. They also have applications in science and engineering fields, including astronomy and architecture.

Before moving on with this section, make sure to review angle properties and types of angles. A quick review of triangles might also help.

This section covers:

• What is an Acute Angle?
• Acute Triangles
• Complementary Angles
• Acute Angle Definition
• Acute Angle Example

What is an Acute Angle?

An acute angle is an angle with a measure less than the measure of a right angle. Since many systems (including those used for trigonometric functions) make use of negative angles, definitions usually stipulate that an acute angle must also be greater than a zero angle.

In degrees, an acute angle $\alpha$ has a measure between $0$ and $90$ degrees. In radians, the measure of alpha is between $0$ and $\frac{\pi}{2}$ radians.

An easy mnemonic for remembering the definition of acute in English stems from the common use of the word “cute” to describe something small, like a puppy. Consequently, acute angles are small angles.

Acute Triangle

All triangles have at least two acute angles.

This is because a triangle with two right angles has a third angle with a measure of $0$, so such a “triangle” is actually a straight line. If a triangle has two or more obtuse angles, its interior angle measure exceeds $180$ degrees.

The measure of the third angle, therefore, is used to classify triangles by angle types. If the third angle is greater than a right angle, the triangle is obtuse. Likewise, if the third angle is right, then the triangle is right.

If, however, all three angles are acute, then the triangle is an acute triangle. This can happen if, for example, each angle is $60$ degrees in measure. Such a triangle has an interior angle measure of $180$ degrees, but the individual angles are each smaller than a right angle.

Complementary Angles

Complementary angles are two angles that, together, have the measure of a right angle.

Assuming both angles are positive, two complementary angles will both be acute.

Acute Angle Definition

An acute angle is an angle less than a right angle but greater than a zero angle.

Such an angle has a measure between $0$ and $90$ degrees not inclusive or between $0$ and $\frac{\pi}{2}$ radians not inclusive.

Acute Angle Example

There are infinitely many acute angles since there are infinitely many numbers between $0$ and $90$ or $0$ and $\frac{\pi}{2}$.

In degrees, examples of acute angles include:

• $0.0001$ degrees
• $15$ degrees
• $45$ degrees
• $75$ degrees
• $89.9999$ degrees.

In radians, examples of acute angles include:

• $\frac{1}{1000} \pi$
• $\frac{1}{10} \pi$
• $\frac{3}{8} \pi$
• $\frac{2}{5} \pi$
• $\frac{49}{100} \pi$.

Common Examples

This section covers common examples of problems involving acute angles and their step-by-step solutions.

Example 1

Classify each angle as acute or not acute.

A. $\frac{27}{53} \pi$ radians

B. $\frac{23}{51} \pi$ radians

C. $-2$ degrees

D. $2$ degrees

Solution

In this case, angles B and D are acute while angles A and C are not.

For problems involving radians, look at the coefficient of $\pi$. If it is less than $\frac{1}{2}$ and greater than $0$, the angle is acute.

In this case, consider $\frac{27}{53}$. Half of $53$ is $26.5$. Since $27 > 26.5$, $\frac{27}{53}$ is greater than $\frac{1}{2}$. Thus, $\frac{27}{53} \pi$ is greater than $\frac{\pi}{2}$. Therefore, the angle is obtuse.

But, half of $51$ is $25.5$. Since $23$ is less than $25.5$, $\frac{23}{51}$ is less than one half. Therefore, $\frac{23}{51} \pi$ is less than $\frac{\pi}{2}$, so the angle B is acute.

C is a negative degree measure. This means the angle is less than a zero angle, so it is not acute. Note that this only matter when the orientation of the angle in space matters or when used algebraically.

The last angle, D, however, is between $0$ and $90$ degrees not inclusive. Therefore, it is acute.

Example 2

Is the following triangle acute? Why or why not?

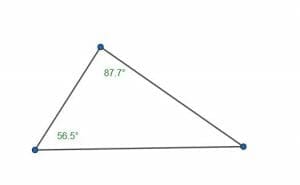
Solution

This triangle is acute.

Although only two angles are given, the information is sufficient to determine that the third angle is acute. Since the given two angles are also acute, all three angles are acute. Consequently, the triangle is acute.

Why?

Recall that the interior angle measures of a triangle (in degrees) add up to $180$ degrees. This means that the measure of the third angle is equal to $180-(87.7+56.5) = 180-144.2 = 35.8$ degrees.

Since $35.8$, $56.5$, and $87.7$ are all less than $90$ degrees, the triangle must be acute.

Example 3

Find the angle complement for an angle with a measure of $\frac{4}{9} \pi$ radians.

Solution

The angle complement of an angle is another angle that can be added to the first to create a right angle.

The given angle $\frac{4}{9} \pi$ radians is smaller than a right angle because $4$ is less than $4.5$, and $\frac{4.5}{9} \pi = \frac{1}{2} \pi$ radians, the measure of a right angle in radians.

In this case then, the complement is the difference between $\frac{\pi}{2}$ radians and $\frac{4}{9} \pi$ radians.

This is equal to:

$\frac{4.5}{9} \pi – \frac{4}{9} \pi = \frac{0.5}{9} \pi = \frac{1}{18} \pi$.

Thus, the angle complement has a measure of $\frac{1}{18} \pi$ radians.

Example 4

What is the fewest number of acute angles necessary to create a straight angle?

Solution

Recall that a straight angle is equal in measure to two right angles. In degrees, it is $180$ degrees. It is also equal to $\pi$ radians.

Since each acute angle is less than $90$ degrees or $\frac{\pi}{2}$ radians, two acute angles must have an angle measure less than $180$ degrees or less than $\pi$ radians.

That is, two acute angles will always be smaller than a straight angle. But, two acute angles close to a right angle plus one small angle could equal a straight line.

For example, two angles with measure $89$ degrees and $88$ degrees have a sum of $177$ degrees. An additional $3$ degree angle would create a straight line.

Similarly, a $\frac{49}{100} \pi$ radians angle and a $\frac{47}{100} \pi$ radians angle have a total measure of $\frac{97}{100} \pi$ radians. But, an additional $\frac{3}{100} \pi$ radians angle would be sufficient to create a straight line.

Example 5

Consider a circle with a center $A$ and two distinct points $B$ and $C$ on the circumference.

Prove that the angle $ACB$ is acute for any point $C$ on the circumference of the triangle.

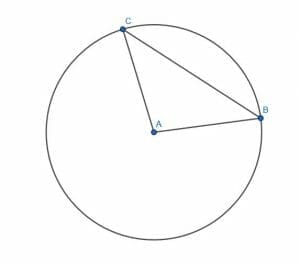
Solution

First, note that the line segments $AC$ and $AB$ have the same length because both are radii of the same circle.

Therefore, the triangle $ABC$ will always be at least isosceles and sometimes equilateral.

But, an isosceles triangle always has equal base angles. This means that the angles $ACB$ and $ABC$ will always be equal, no matter where $C$ is on the circumference.

These two angles cannot be obtuse because the total internal angle measure of the triangle would then be greater than two right angles.

Similarly, the two angles cannot both be right because then the angle $CAB$ would be a zero angle. This means that $C$ and $B$ would have to lie on the same line on the same side of $A$ and on the circumference. Then, in such a case, $C$ and $B$ would be the same point. The set up for this problem, however, states that $C$ and $B$ must be distinct points.

Therefore, both angles must be acute. In particular, then $ACB$ is acute for any distinct point $C$ on the circumference.

More Examples with Explanation

1. A triangle has two angles whose degrees total $91$ degrees. Is the triangle acute? Why or why not? Can you use this example to make a general rule for determining whether or not a triangle is acute based on two angle measures?
2. What is the minimum number of acute angles needed to make a circle?
3. Prove that the only possible acute polygon is a triangle. That is, prove that for any n-gon with more than three sides, it is impossible for all of the angles to be acute.
4. Let $ABC$ be a triangle where the angle $ABC$ is greater than the angle $BCA$. Prove that $BCA$ is an acute angle.
5. Prove that the angle supplement of any obtuse angle is acute.

Answer Key

1. This triangle is not necessarily acute. Though the third angle is $180-91 = 89$ degrees and therefore acute, it was never specified that the smaller angles totaled $91$ degrees. It is possible the triangle is right. For example, it could have a right angle and a $1$ degree angle. It could even be obtuse because degree measures ar continuous. If it had, for example, an angle with a measure of $0.5$ and another of $90.5$ degrees, it would be obtuse.
   But, if two acute angles total to $91$ degrees, then the triangle is acute. In general, if the two smaller angles of a triangle (which must always be acute) have a measure greater than the measure of a right angle, the triangle is acute.
2. $5$ acute angles are needed.
3. Prove this by contradiction. Let $n$ be a natural number greater than or equal to $4$. Then the sum of the interior angles must be equal to $180(n-2) = 180n-360$.
   Suppose all the angles of the n-gon are less than a right angle. In degrees, their measure is less than $90$ degrees. Then, the sum of the interior angles, $\alpha$, is less than $90n$.
   But the sum of the interior angles is equal to $180n-360$. Therefore, $180n-360 < 90n$. Moving the $n$ terms to the left and other terms to the right gives $90n < 360$. Then, dividing yields $n<4$.
   But, the only polygon with fewer than $4$ sides is a triangle. Therefore, the only acute polygon is a triangle.
4. The smallest two angles of every triangle are acute. Therefore, $ABC$ is either the greater of the two acute angles and $BCA$ is the smaller of the two or $ABC$ is the largest angle in the triangle and $BCA$ is one of the two smaller, acute angles. In the latter case, regardless of whether $ABC$ is acute, obtuse, or right, $BCA$ is still acute. In the former case, $BCA$ is also acute. Therefore, the angle must be acute if it is not the largest angle.
5. An obtuse angle measures greater than a right angle and an angle supplement works together with another angle to make a straight angle. In degrees, a straight angle has $180$ degrees. The supplement of any angle measures $180-\alpha$. If $\alpha$ is obtuse, then $\alpha > 90$ degrees. Therefore, $180-\alpha < 90$. Thus, the supplement is less than $90$ degrees and consequently obtuse.

Images/mathematical drawings are created with GeoGebra.