RENé DESCARTES: Father of Modern Philosophy
 |
René Descartes (1596-1650) |
Biography – Who is Descartes
René Descartes has been dubbed the “Father of Modern Philosophy“, but he was also one of the key figures in the Scientific Revolution of the 17th Century, and is sometimes considered the first of the modern school of mathematics.
As a young man, he found employment for a time as a soldier (essentially as a mercenary in the pay of various forces, both Catholic and Protestant). But, after a series of dreams or visions, and after meeting the Dutch philosopher and scientist Isaac Beeckman, who sparked his interest in mathematics and the New Physics, he concluded that his real path in life was the pursuit of true wisdom and science.
Back in France, the young Descartes soon came to the conclusion that the key to philosophy, with all its uncertainties and ambiguity, was to build it on the indisputable facts of mathematics. To pursue his rather heretical ideas further, though, he moved from the restrictions of Catholic France to the more liberal environment of the Netherlands, where he spent most of his adult life, and where he worked on his dream of merging algebra and geometry.
In 1637, he published his ground-breaking philosophical and mathematical treatise “Discours de la méthode” (the “Discourse on Method”), and one of its appendices in particular, “La Géométrie”, is now considered a landmark in the history of mathematics. Following on from early movements towards the use of symbolic expressions in mathematics by Diophantus, Al-Khwarizmi and François Viète, “La Géométrie” introduced what has become known as the standard algebraic notation, using lowercase a, b and c for known quantities and x, y and z for unknown quantities. It was perhaps the first book to look like a modern mathematics textbook, full of a‘s and b‘s, x2‘s, etc.
Cartesian Coordinate System
 |
Cartesian Coordinates |
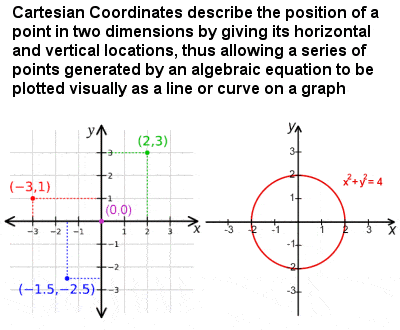
It was in “La Géométrie” that Descartes first proposed that each point in two dimensions can be described by two numbers on a plane, one giving the point’s horizontal location and the other the vertical location, which have come to be known as Cartesian coordinates. He used perpendicular lines (or axes), crossing at a point called the origin, to measure the horizontal (x) and vertical (y) locations, both positive and negative, thus effectively dividing the plane up into four quadrants.
Any equation can be represented on the plane by plotting on it the solution set of the equation. For example, the simple equation y = x yields a straight line linking together the points (0,0), (1,1), (2,2), (3,3), etc. The equation y = 2x yields a straight line linking together the points (0,0), (1,2), (2,4), (3,6), etc. More complex equations involving x2, x3, etc, plot various types of curves on the plane.
As a point moves along a curve, then, its coordinates change, but an equation can be written to describe the change in the value of the coordinates at any point in the figure. Using this novel approach, it soon became clear that an equation like x2 + y2 = 4, for example, describes a circle; y2 – 16x a curve called a parabola; x2⁄a2 + y2⁄b2 = 1 an ellipse; x2⁄a2 – y2⁄b2 = 1 a hyperbola; etc.
Descartes’ ground-breaking work, usually referred to as analytic geometry or Cartesian geometry, had the effect of allowing the conversion of geometry into algebra (and vice versa). Thus, a pair of simultaneous equations could now be solved either algebraically or graphically (at the intersection of two lines). It allowed the development of Newton’s and Leibniz’s subsequent discoveries of calculus. It also unlocked the possibility of navigating geometries of higher dimensions, impossible to physically visualize – a concept which was to become central to modern technology and physics – thus transforming mathematics forever.
Rule of Signs
 |
Descartes’ Rule of Signs |
Although analytic geometry was far and away Descartes’ most important contribution to mathematics, he also: developed a “rule of signs” technique for determining the number of positive or negative real roots of a polynomial; “invented” (or at least popularized) the superscript notation for showing powers or exponents (e.g. 24 to show 2 x 2 x 2 x 2); and re-discovered Thabit ibn Qurra’s general formula for amicable numbers, as well as the amicable pair 9,363,584 and 9,437,056 (which had also been discovered by another Islamic mathematician, Yazdi, almost a century earlier).
For all his importance in the development of modern mathematics, though, Descartes is perhaps best known today as a philosopher who espoused rationalism and dualism. His philosophy consisted of a method of doubting everything, then rebuilding knowledge from the ground, and he is particularly known for the often-quoted statement “Cogito ergo sum”(“I think, therefore I am”).
He also had an influential rôle in the development of modern physics, a rôle which has been, until quite recently, generally under-appreciated and under-investigated. He provided the first distinctly modern formulation of laws of nature and a conservation principle of motion, made numerous advances in optics and the study of the reflection and refraction of light, and constructed what would become the most popular theory of planetary motion of the late 17th Century. His commitment to the scientific method was met with strident opposition by the church officials of the day.
His revolutionary ideas made him a centre of controversy in his day, and he died in 1650 far from home in Stockholm, Sweden. 13 years later, his works were placed on the Catholic Church’s “Index of Prohibited Books”.
<< Back to 17th Century Mathematics | Forward to Fermat >> |
