BERNOULLI BROTHERS – THE MATH FAMILY
 |
Jacob (1654-1705) and Johann Bernoulli (1667-1748) |
Unusually in the history of mathematics, a single family, the Bernoulli’s, produced half a dozen outstanding mathematicians over a couple of generations at the end of the 17th and start of the 18th Century.
The Bernoulli family was a prosperous family of traders and scholars from the free city of Basel in Switzerland, which at that time was the great commercial hub of central Europe.The brothers, Jacob and Johann Bernoulli, however, flouted their father’s wishes for them to take over the family spice business or to enter respectable professions like medicine or the ministry, and began studying mathematics together.
After Johann graduated from Basel University, the two developed a rather jealous and competitive relationship. Johann in particular was jealous of the elder Jacob’s position as professor at Basel University, and the two often attempted to outdo each other. After Jacob’s early death from tuberculosis, Johann took over his brother’s position, one of his young students being the great Swiss mathematician Leonhard Euler. However, Johann merely shifted his jealousy toward his own talented son, Daniel (at one point, Johann published a book based on Daniel’s work, even changing the date to make it look as though his book had been published before his son’s).
Johann received a taste of his own medicine, though, when his student Guillaume de l’Hôpital published a book in his own name consisting almost entirely of Johann’s lectures, including his now famous rule about 0 ÷ 0 (a problem which had dogged mathematicians since Brahmagupta‘s initial work on the rules for dealing with zero back in the 7th Century). This showed that 0 ÷ 0 does not equal zero, does not equal 1, does not equal infinity, and is not even undefined, but is “indeterminate” (meaning it could equal any number). The rule is still usually known as l’Hôpital’s Rule, and not Bernoulli’s Rule.
Despite their competitive and combative personal relationship, though, the brothers both had a clear aptitude for mathematics at a high level, and constantly challenged and inspired each other. They established an early correspondence with Gottfried Leibniz, and were among the first mathematicians to not only study and understand infinitesimal calculus but to apply it to various problems. They became instrumental in disseminating the newly-discovered knowledge of calculus, and helping to make it the cornerstone of mathematics it has become today.
Brachistochrone Problem
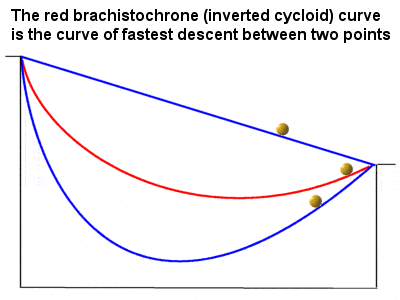 |
The Bernoulli’s first derived the brachistochrone curve, using his calculus of variation method |
But they were more than just disciples of Leibniz, and they also made their own important contributions. One well known and topical problem of the day to which they applied themselves was that of designing a sloping ramp which would allow a ball to roll from the top to the bottom in the fastest possible time. Johann Bernoulli demonstrated through calculus that neither a straight ramp or a curved ramp with a very steep initial slope were optimal, but actually a less steep curved ramp known as a brachistochrone curve (a kind of upside-down cycloid, similar to the path followed by a point on a moving bicycle wheel) is the curve of fastest descent.
This application was an example of the “calculus of variations”, a generalization of infinitesimal calculus that the Bernoulli brothers developed together, and has since proved useful in fields as diverse as engineering, financial investment, architecture and construction, and even space travel. Johann also derived the equation for a catenary curve, such as that formed by a chain hanging between two posts, a problem presented to him by his brother Jacob.
The Art of Conjecture: Trials, Distribution, Numbers
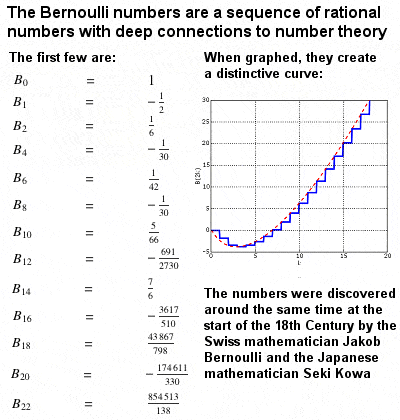 |
Bernoulli Numbers |
Jacob Bernoulli’s book “The Art of Conjecture”, published posthumously in 1713, consolidated existing knowledge on probability theory and expected values, as well as adding personal contributions, such as his theory of permutations and combinations, Bernoulli trials and Bernoulli distribution, and some important elements of number theory, such as the Bernoulli Numbers sequence. He also published papers on transcendental curves, and became the first person to develop the technique for solving separable differential equations (the set of non-linear, but solvable, differential equations are now named after him). He invented polar coordinates (a method of describing the location of points in space using angles and distances) and was the first to use the word “integral” to refer to the area under a curve.
Jacob Bernoulli also discovered the appropximate value of the irrational number e while exploring the compound interest on loans. When compounded at 100% interest annually, $1.00 becomes $2.00 after one year; when compounded semi-annually it ppoduces $2.25; compounded quarterly $2.44; monthly $2.61; weekly $2.69; daily $2.71; etc. If it were to be compounded continuously, the $1.00 would tend towards a value of $2.7182818… after a year, a value which became known as e. Alegbraically, it is the value of the infinite series (1 + 1⁄1)1.(1 + 1⁄2)2.(1 + 1⁄3)3.(1 + 1⁄4)4…
Johann’s sons Nicolaus, Daniel and Johann II, and even his grandchildren Jacob II and Johann III, were all accomplished mathematicians and teachers. Daniel Bernoulli, in particular, is well known for his work on fluid mechanics (especially Bernoulli’s Principle on the inverse relationship between the speed and pressure of a fluid or gas), as much as for his work on probability and statistics.
<< Back to 18th Century Mathematics | Forward to Euler >> |
