ALAN TURING: CRACKING THE ‘ENIGMA’ CODE
Biography
 |
Alan Turing (1912-1954) |
The British mathematician Alan Turing is perhaps most famous for his war-time work at the British code-breaking centre at Bletchley Park where his work led to the breaking of the German enigma code (according to some, shortening the Second World War at a stroke, and potentially saving thousands of lives). But he was also responsible for making Gödel’s already devastating incompleteness theorem even more bleak and discouraging, and it is mainly on this – and the development of computer science that his work gave rise to – that Turing’s mathematical legacy rests.
Despite attending an expensive private school which strongly emphasized the classics rather than the sciences, Turing showed early signs of the genius which was to become more prominent later, solving advanced problems as a teenager without having even studied elementary calculus, and immersing himself in the complex mathematics of Albert Einstein’s work. He became a confirmed atheist after the death of his close friend and fellow Cambridge student Christopher Morcom, and throughout his life he was an accomplished and committed long-distance runner.
In the years following the publication of Gödel’s incompleteness theorem, Turing desperately wanted to clarify and simplify Gödel’s rather abstract and abstruse theorem, and to make it more concrete. But his solution – which was published in 1936 and which, he later claimed, had come to him in a vision – effectively involved the invention of something that has come to shape the entire modern world, the computer.
Turing Machine
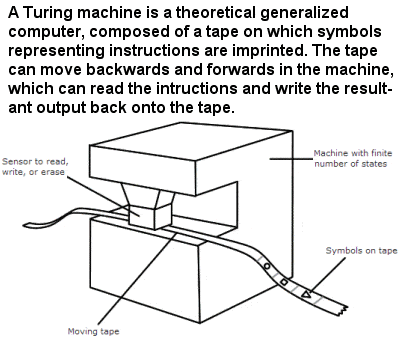 |
Representation of a Turing Machine |
During the 1930s, Turing recast incompleteness in terms of computers (or, more specifically, a theoretical device that manipulates symbols, known as a Turing machine), replacing Gödel‘s universal arithmetic-based formal language with this formal and simple device. He first proved that such a machine would be capable of performing any conceivable mathematical computation if it were representable as an algorithm. He then went on to show that, even for such a logical machine, essentially driven by arithmetic, there would always be some problems they would never be able to solve, and that a machine fed such a problem would never stop trying to solve it, but would never succeed (known as the “halting problem”).
In the process, he also proved that there was no way of telling beforehand which problems were the unprovable ones, thus providing a negative proof to the so-called Entscheidungsproblem or “decision problem“, posed by David Hilbert in 1928. This was a further slap in the face for a mathematics community still reeling from Gödel’s crushing incompleteness theorem.
After the war, Turing continued the work he had begun, and worked on the development of early computers such as ACE (Automatic Computing Engine) and the Manchester Mark 1. Although the computer he developed was a very basic and limited machine by modern standards, Turing clearly saw its potential, and dreamed that one day computers would be more than machines, capable of learning, thinking and communicating. He was the first to develop ideas for a chess-playing computer program, and saw mastery in the game as one of the goals that designers of intelligent machines should strive for.
Turing test
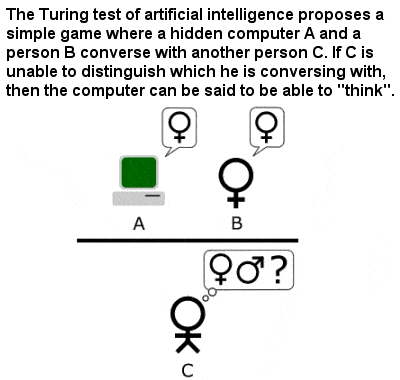 |
Turing test |
Indeed, he was the first to address the problem of artificial intelligence, and proposed an experiment now known as the Turing Test in an attempt to define a standard for a machine to be called “intelligent“. By this test, a computer could be said to “think” if it could fool a human interrogator into thinking that the conversation was with a human. This showed remarkable foresight at a time long before the Internet, when the only available computers were the size of a room and less powerful than a modern pocket calculator.
Turing’s personal philosophy was to be free from hypocrisy, compromise and deceit. He was, for example, a homosexual at a time when it was both illegal and even dangerous, yet he never hid it nor made it an issue. Unlike Gödel (who strongly believed in the power of intuition, and who was convinced that the human mind was capable of going beyond the limitations of the systems he described), Turing clearly felt a certain affinity with computers and, to some extent, he saw them as embodying this admirable absence of lies or hypocrisy.
After the war, he was kept under surveillance as a potential security risk by the authorities and eventually, in 1952, he was arrested, charged and found guilty of engaging in a homosexual act. As a result, he was chemically castrated by an injection of the female hormone estrogen, which caused him to grow breasts and also affected his mind. In 1954, Turing was found dead, apparently having committed suicide with cyanide.
<< Back to Gödel | Forward to Weil >> |
