HELLENISTIC MATHEMATICS
 |
The Sieve of Eratosthenes |
By the 3rd Century BCE, in the wake of the conquests of Alexander the Great, mathematical breakthroughs were also beginning to be made on the edges of the Greek Hellenistic empire.
In particular, Alexandria in Egypt became a great centre of learning under the beneficent rule of the Ptolemies, and its famous Library soon gained a reputation to rival that of the Athenian Academy. The patrons of the Library were arguably the first professional scientists, paid for their devotion to research. Among the best known and most influential mathematicians who studied and taught at Alexandria were Euclid, Archimedes, Eratosthenes, Heron, Menelaus and Diophantus.
During the late 4th and early 3rd Century BCE, Euclid was the great chronicler of the mathematics of the time, and one of the most influential teachers in history. He virtually invented classical (Euclidean) geometry as we know it. Archimedes spent most of his life in Syracuse, Sicily, but also studied for a while in Alexandria. He is perhaps best known as an engineer and inventor but, in the light of recent discoveries, he is now considered of one of the greatest pure mathematicians of all time. Eratosthenes of Alexandria was a near contemporary of Archimedes in the 3rd Century BCE. A mathematician, astronomer and geographer, he devised the first system of latitude and longitude, and calculated the circumference of the earth to a remarkable degree of accuracy. As a mathematician, his greatest legacy is the “Sieve of Eratosthenes” algorithm for identifying prime numbers.
Spherical Triangle
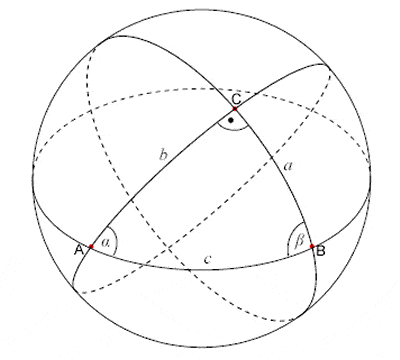 |
Menelaus of Alexandria introduced the concept of the spherical triangle |
It is not known exactly when the great Library of Alexandria burned down, but Alexandria remained an important intellectual centre for some centuries. In the 1st century BCE, Heron (or Hero) was another great Alexandrian inventor, best known in mathematical circles for Heronian triangles (triangles with integer sides and integer area), Heron’s Formula for finding the area of a triangle from its side lengths, and Heron’s Method for iteratively computing a square root. He was also the first mathematician to confront at least the idea of √-1 (although he had no idea how to treat it, something which had to wait for Tartaglia and Cardano in the 16th Century).
Menelaus of Alexandria, who lived in the 1st – 2nd Century CE, was the first to recognize geodesics on a curved surface as the natural analogues of straight lines on a flat plane. His book “Sphaerica” dealt with the geometry of the sphere and its application in astronomical measurements and calculations, and introduced the concept of spherical triangle (a figure formed of three great circle arcs, which he named “trilaterals“).
In the 3rd Century CE, Diophantus of Alexandria was the first to recognize fractions as numbers, and is considered an early innovator in the field of what would later become known as algebra. He applied himself to some quite complex algebraic problems, including what is now known as Diophantine Analysis, which deals with finding integer solutions to kinds of problems that lead to equations in several unknowns (Diophantine equations). Diophantus’ “Arithmetica”, a collection of problems giving numerical solutions of both determinate and indeterminate equations, was the most prominent work on algebra in all Greek mathematics, and his problems exercised the minds of many of the world’s best mathematicians for much of the next two millennia.
Conic Sections of Apollonius
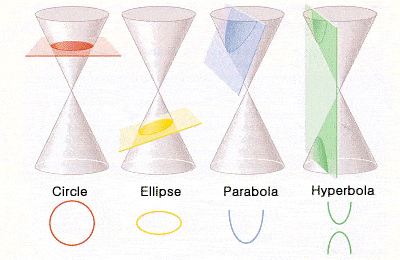 |
Conic sections of Apollonius |
But Alexandria was not the only centre of learning in the Hellenistic Greek empire. Mention should also be made of Apollonius of Perga (a city in modern-day southern Turkey) whose late 3rd Century BCE work on geometry (and, in particular, on conics and conic sections) was very influential on later European mathematicians. It was Apollonius who gave the ellipse, the parabola, and the hyperbola the names by which we know them, and showed how they could be derived from different sections through a cone.
Hipparchus, who was also from Hellenistic Anatolia and who live in the 2nd Century BCE, was perhaps the greatest of all ancient astronomers. He revived the use of arithmetic techniques first developed by the Chaldeans and Babylonians, and is usually credited with the beginnings of trigonometry. He calculated (with remarkable accuracy for the time) the distance of the moon from the earth by measuring the different parts of the moon visible at different locations and calculating the distance using the properties of triangles. He went on to create the first table of chords (side lengths corresponding to different angles of a triangle). By the time of the great Alexandrian astronomer Ptolemy in the 2nd Century CE, however, Greek mastery of numerical procedures had progressed to the point where Ptolemy was able to include in his “Almagest” a table of trigonometric chords in a circle for steps of ¼° which (although expressed sexagesimally in the Babylonian style) is accurate to about five decimal places.
By the middle of the 1st Century BCE and thereafter, however, the Romans had tightened their grip on the old Greek empire. The Romans had no use for pure mathematics, only for its practical applications, and the Christian regime that followed it even less so. The final blow to the Hellenistic mathematical heritage at Alexandria might be seen in the figure of Hypatia, the first recorded female mathematician, and a renowned teacher who had written some respected commentaries on Diophantus and Apollonius. She was dragged to her death by a Christian mob in 415 CE.
<< Back to Plato | Forward to Euclid >> |
