LEONARDO FIBONACCI – ITALIAN MATHEMATICIAN (WROTE LEBER ABACI)
 |
Leonardo of Pisa (Fibonacci) (c.1170-1250) |
The 13th Century Italian Leonardo of Pisa, better known by his nickname Fibonacci, was perhaps the most talented Western mathematician of the Middle Ages. Little is known of his life except that he was the son of a customs offical and, as a child, he travelled around North Africa with his father, where he learned about Arabic mathematics. On his return to Italy, he helped to disseminate this knowledge throughout Europe, thus setting in motion a rejuvenation in European mathematics, which had lain largely dormant for centuries during the Dark Ages.
In particular, in 1202, he wrote a hugely influential book called “Liber Abaci” (“Book of Calculation”), in which he promoted the use of the Hindu-Arabic numeral system, describing its many benefits for merchants and mathematicians alike over the clumsy system of Roman numerals then in use in Europe. Despite its obvious advantages, uptake of the system in Europe was slow (this was after all during the time of the Crusades against Islam, a time in which anything Arabic was viewed with great suspicion), and Arabic numerals were even banned in the city of Florence in 1299 on the pretext that they were easier to falsify than Roman numerals. However, common sense eventually prevailed and the new system was adopted throughout Europe by the 15th century, making the Roman system obsolete. The horizontal bar notation for fractions was also first used in this work (although following the Arabic practice of placing the fraction to the left of the integer).
Fibonacci Sequence
 |
The discovery of the famous Fibonacci sequence |
Fibonacci is best known, though, for his introduction into Europe of a particular number sequence, which has since become known as Fibonacci Numbers or the Fibonacci Sequence. He discovered the sequence – the first recursive number sequence known in Europe – while considering a practical problem in the “Liber Abaci” involving the growth of a hypothetical population of rabbits based on idealized assumptions. He noted that, after each monthly generation, the number of pairs of rabbits increased from 1 to 2 to 3 to 5 to 8 to 13, etc, and identified how the sequence progressed by adding the previous two terms (in mathematical terms, Fn = Fn-1 + Fn-2), a sequence which could in theory extend indefinitely.
The sequence, which had actually been known to Indian mathematicians since the 6th Century, has many interesting mathematical properties, and many of the implications and relationships of the sequence were not discovered until several centuries after Fibonacci’s death. For instance, the sequence regenerates itself in some surprising ways: every third F-number is divisible by 2 (F3 = 2), every fourth F-number is divisible by 3 (F4 = 3), every fifth F-number is divisible by 5 (F5 = 5), every sixth F-number is divisible by 8 (F6 = 8), every seventh F-number is divisible by 13 (F7 = 13), etc. The numbers of the sequence has also been found to be ubiquitous in nature: among other things, many species of flowering plants have numbers of petals in the Fibonacci Sequence; the spiral arrangements of pineapples occur in 5s and 8s, those of pinecones in 8s and 13s, and the seeds of sunflower heads in 21s, 34s, 55s or even higher terms in the sequence; etc.
The Golden Ratio φ
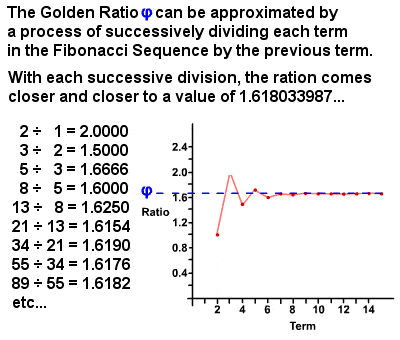 |
The Golden Ratio φ can be derived from the Fibonacci Sequence |
In the 1750s, Robert Simson noted that the ratio of each term in the Fibonacci Sequence to the previous term approaches, with ever greater accuracy the higher the terms, a ratio of approximately 1 : 1.6180339887 (it is actually an irrational number equal to (1 + √5)⁄2 which has since been calculated to thousands of decimal places). This value is referred to as the Golden Ratio, also known as the Golden Mean, Golden Section, Divine Proportion, etc, and is usually denoted by the Greek letter phi φ (or sometimes the capital letter Phi Φ). Essentially, two quantities are in the Golden Ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The Golden Ratio itself has many unique properties, such as 1⁄φ = φ – 1 (0.618…) and φ2 = φ + 1 (2.618…), and there are countless examples of it to be found both in nature and in the human world.
A rectangle with sides in the ratio of 1 : φ is known as a Golden Rectangle, and many artists and architects throughout history (dating back to ancient Egypt and Greece, but particularly popular in the Renaissance art of Leonardo da Vinci and his contemporaries) have proportioned their works approximately using the Golden Ratio and Golden Rectangles, which are widely considered to be innately aesthetically pleasing. An arc connecting opposite points of ever smaller nested Golden Rectangles forms a logarithmic spiral, known as a Golden Spiral. The Golden Ratio and Golden Spiral can also be found in a surprising number of instances in Nature, from shells to flowers to animal horns to human bodies to storm systems to complete galaxies.
It should be remembered, though, that the Fibonacci Sequence was actually only a very minor element in “Liber Abaci” – indeed, the sequence only received Fibonacci’s name in 1877 when Eduouard Lucas decided to pay tribute to him by naming the series after him – and that Fibonacci himself was not responsible for identifying any of the interesting mathematical properties of the sequence, its relationship to the Golden Mean and Golden Rectangles and Spirals, etc.
Lattice Multiplication
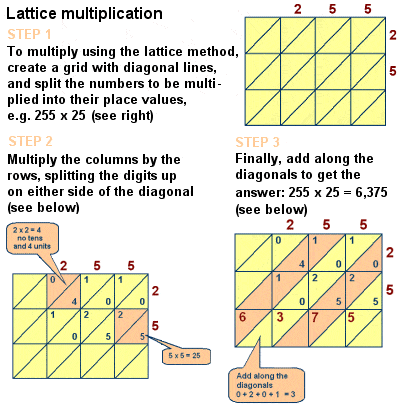 |
Fibonacci introduced lattice multiplication to Europe |
However, the book’s influence on medieval mathematics is undeniable, and it does also include discussions of a number of other mathematical problems such as the Chinese Remainder Theorem, perfect numbers and prime numbers, formulas for arithmetic series and for square pyramidal numbers, Euclidean geometric proofs, and a study of simultaneous linear equations along the lines of Diophantus and Al-Karaji. He also described the lattice (or sieve) multiplication method of multiplying large numbers, a method – originally pioneered by Islamic mathematicians like Al-Khwarizmi – algorithmically equivalent to long multiplication.
Neither was “Liber Abaci” Fibonacci’s only book, although it was his most important one. His “Liber Quadratorum” (“The Book of Squares”), for example, is a book on algebra, published in 1225 in which appears a statement of what is now called Fibonacci’s identity – sometimes also known as Brahmagupta’s identity after the much earlier Indian mathematician who also came to the same conclusions – that the product of two sums of two squares is itself a sum of two squares e.g. (12 + 42)(22 + 72) = 262 + 152 = 302 + 12.
<< Back to Medieval Mathematics | Forward to 16th Century Mathematics >> |
