BOLYAI AND LOBACHEVSKY & HYPERBOLIC GEOMETRY
 |
János Bolyai (1802-1860) and Nikolai Lobachevsky (1792-1856) |
János Bolyai was a Hungarian mathematician who spent most of his life in a little-known backwater of the Hapsburg Empire, in the wilds of the Transylvanian mountains of modern-day Romania, far from the mainstream mathematical communities of Germany, France and England. No original portrait of Bolyai survives, and the picture that appears in many encyclopedias and on a Hungarian postage stamp is known to be unauthentic.
His father and teacher, Farkas Bolyai, was himself an accomplished mathematician and had been a student of the great German mathematician Gauss for a time, but the cantankerous Gauss refused to take on the young prodigy János as a student. So, he was forced to join the army in order to earn a living and support his family, although he persevered with his mathematics in his spare time. He was also a talented linguist, speaking nine foreign languages, including Chinese and Tibetan.
Euclid’s parallel postulate
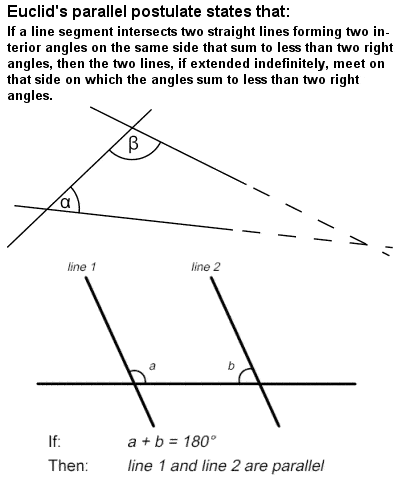 |
Euclid’s parallel postulate |
In particular, Bolyai became obsessed with Euclid‘s fifth postulate (often referred to as the parallel postulate), a fundamental principle of geometry for over two millennia, which essentially states that only one line can be drawn through a given point so that the line is parallel to a given line that does not contain the point, along with its corollary that the interior angles of a triangle sum to 180° or two right angles. In fact, he became obsessed to such an extent that his father warned him that it may take up all his time and deprive him of his “health, peace of mind and happiness in life”, a tragic irony given the unfolding of subsequent events.
Bolyai, however, persisted in his quest, and eventually came to the radical conclusion that it was in fact possible to have consistent geometries that were independent of the parallel postulate. In the early 1820s, Bolyai explored what he called “imaginary geometry” (now known as hyperbolic geometry), the geometry of curved spaces on a saddle-shaped plane, where the angles of a triangle did NOT add up to 180° and apparently parallel lines were NOT actually parallel. In curved space, the shortest distance between two points a and b is actually a curve, or geodesic, and not a straight line. Thus, the angles of a triangle in hyperbolic space sum to less than 180°, and two parallel lines in hyperbolic space actually diverge from each other. In a letter to his father, Bolyai marvelled, “Out of nothing I have created a strange new universe”.
Although it is easy to visualize a flat surface and a surface with positive curvature (e.g. a sphere, such as a the Earth), it is impossible to visualize a hyperbolic surface with negative curvature, other than just over a small localized area, where it would look like a saddle or a Pringle. So the very concept of a hyperbolic surface appeared to go against all sense of reality. It certainly represented a radical departure from Euclidean geometry, and the first step along the road which would lead to Einstein’s Theory of Relativity among other applications (although it still fell well short of the multi-dimensional geometry which was to be later realized by Riemann). Between 1820 and 1823, Bolyai prepared, but did not immediately publish, a treatise on a complete system of non-Euclidean geometry.
His work was, however, only published in 1832, and then only a short exposition in the appendix of a textbook by his father. On reading this, Gauss clearly recognized the genius of the younger Bolyai’s ideas, but he refused to encourage the young man, and even tried to claim his ideas as his own. Further disheartened by the news that the Russian mathematician Lobachevski had published something quite similar two years before his own paper, Bolyai became a recluse and gradually went insane. He died in obscurity in 1860. Although he only ever published the 24 pages of the appendix, Bolyai left more than 20,000 pages of mathematical manuscripts when he died (including the development of a rigorous geometric concept of complex numbers as ordered pairs of real numbers).
Hyperbolic Bolyai-Lobachevskian geometry
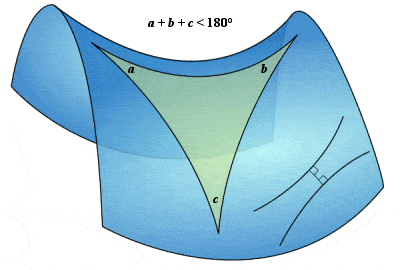 |
Hyperbolic Bolyai-Lobachevskian geometry |
Completely independent from Bolyai, in the distant provincial Russian city of Kazan, Nikolai Ivanovich Lobachevsky had also been working, along very similar lines as Bolyai, to develop a geometry in which Euclid’s fifth postulate did not apply. His work on hyperbolic geometry was first reported in 1826 and published in 1830, although it did not have general circulation until some time later.
This early non-Euclidean geometry is now often referred to as Lobachevskian geometry or Bolyai-Lobachevskian geometry, thus sharing the credit. Gauss’ claims to have originated, but not published, the ideas are difficult to judge in retrospect. Other much earlier claims are credited to the 11th Century Persian mathematician Omar Khayyam, and to the early 18th Century Italian priest Giovanni Saccheri, but their work was much more speculative and inconclusive in nature.
Lobachevsky also died in poverty and obscurity, nearly blind and unable to walk. Among his other mathematical achievements, largely unknown during his lifetime, was the development of a method for approximating the roots of algebraic equations (a method now known as the Dandelin-Gräffe method, named after two other mathematicians who discovered it independently), and the definition of a function as a correspondence between two sets of real numbers (usually credited to Dirichlet, who gave the same definition independently soon after Lobachevsky).
<< Back to Gauss | Forward to Riemann >> |
