JUMP TO TOPIC
2 Times Table – Explanation & Examples
 Multiplication is best understood using tables. For example, when we multiply all natural numbers ($1,2,3,\cdots$, etc.) with $2$ and put the answers in a table, we get the 2 times table.
Multiplication is best understood using tables. For example, when we multiply all natural numbers ($1,2,3,\cdots$, etc.) with $2$ and put the answers in a table, we get the 2 times table.
$2$ times table is a table that contains the multiples of the number$2$
Learning the table of $2$ is the starting point for understanding multiplication as well as the rest of the multiplication tables in mathematics. This article will help students understand and memorize the $2$ times table easily and efficiently.
Students should refresh the following concepts to understand the material discussed in this topic.
- Basics of addition and multiplication
- One times table
Let us take a simple example of a basic addition and multiplication problem, and then we will try to solve it using a $2$ times table.
Example:
Alex has just been promoted to second grade, and he asks his mother to teach him the table of $2$. Alex has a shoe rack in his house, and it contains $5$ pairs of shoes. Alex’s mother asks him to count the total number of shoes present in the shoe rack. Alex calculates the number of shoes using the addition method.
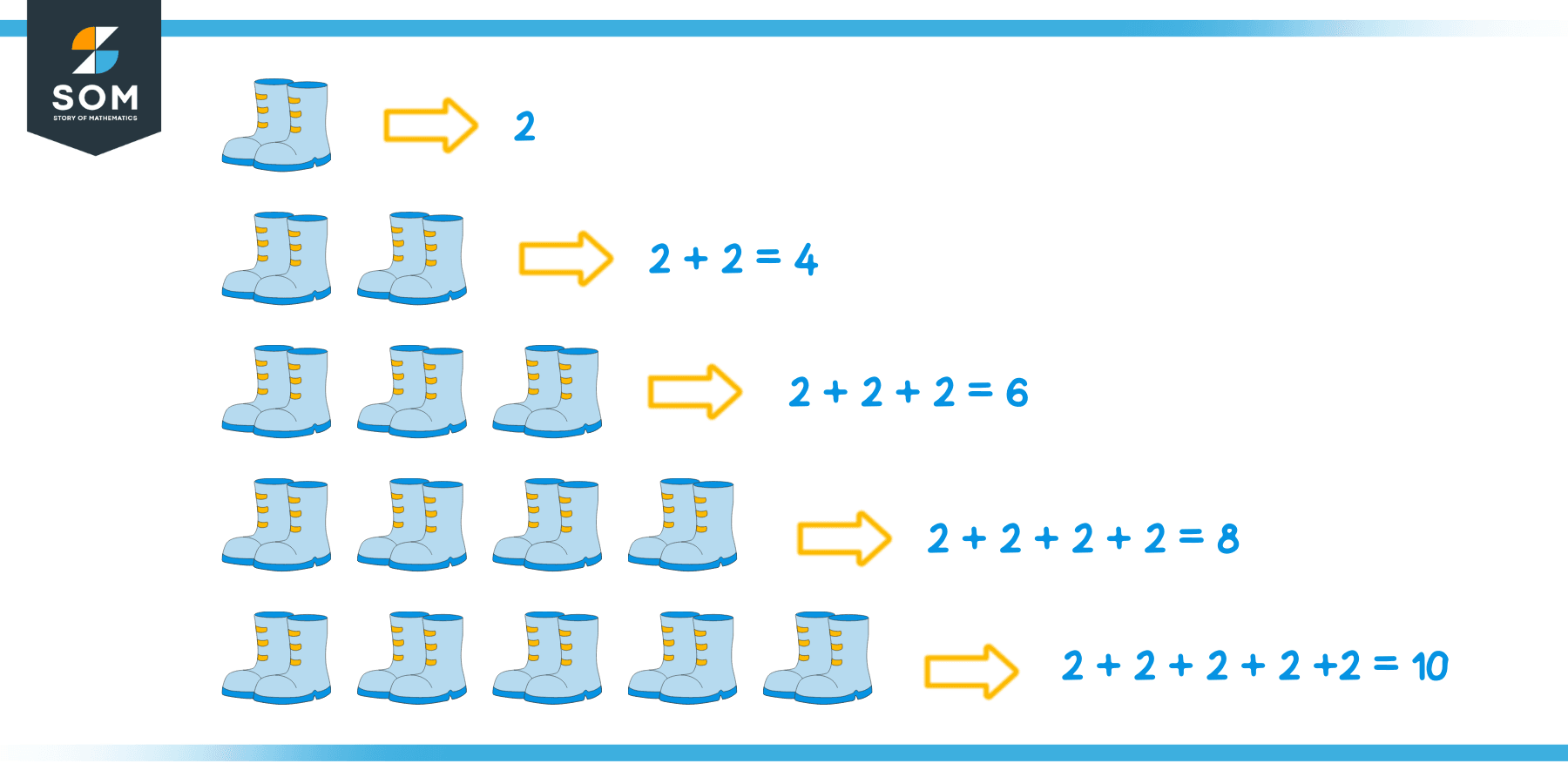
Alex gets to the right answer, which is $10$. But addition can take time, and if we increase the pair of shoes, the calculation will become lengthy. Alex’s mother suggests that he use multiplication instead. A single pair consists of two shoes.
Similarly, two pairs consist of four shoes and so on:
- First pair: $1 \times 2 =2$
- Second pair: $2 \times 2= 4$
- Third pair: $3 \times 2= 6$
- Fourth pair: $4 \times 2 = 8$
- Fifth pair: $5 \times 2= 10$
2 Multiplication Table
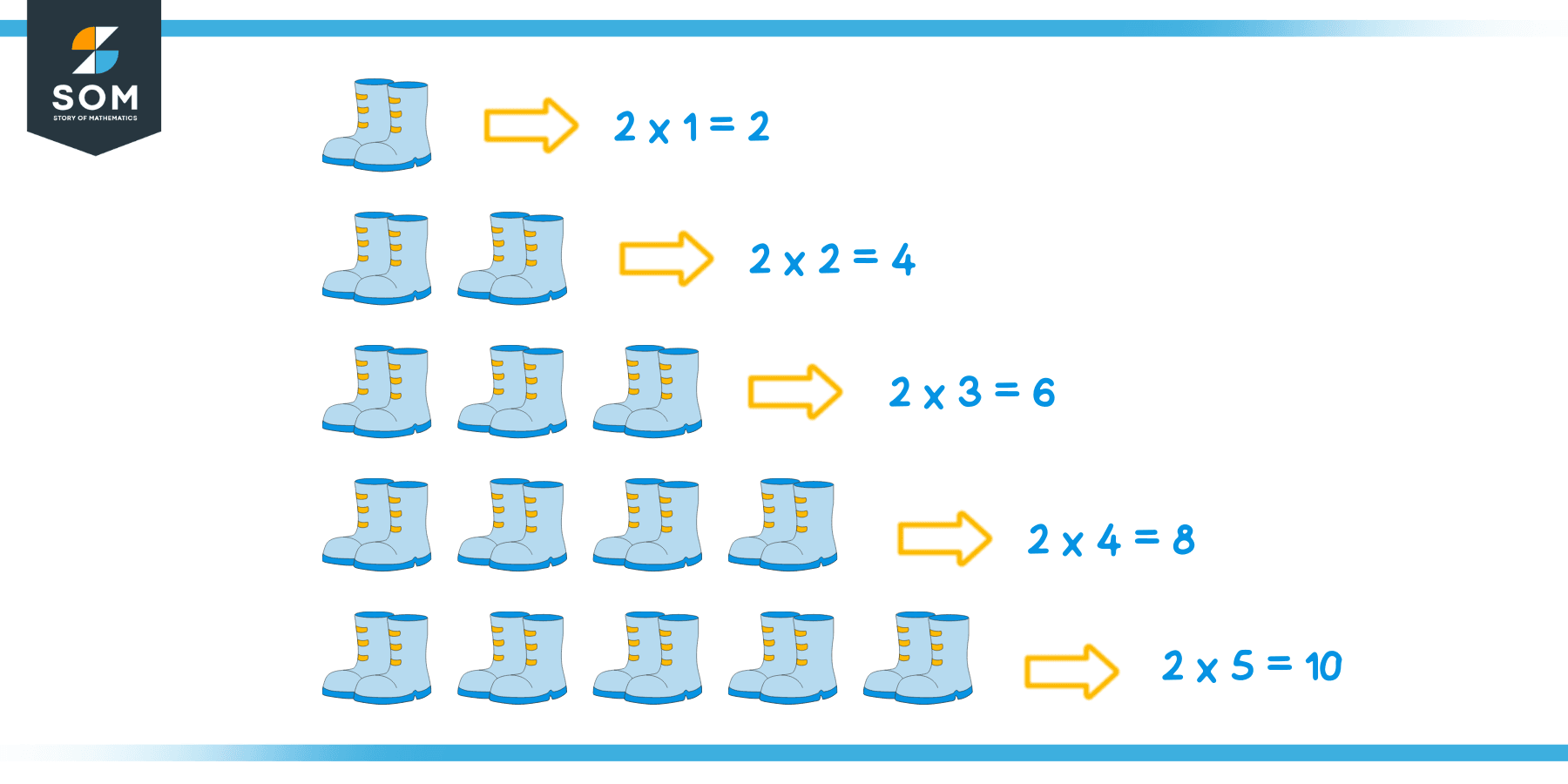
Using the above example, if Alex has $10$ pair of shoes, then the total number of shoes using 2 times table can be calculated as:
- $2\times1 = 2$
- $2\times2 = 4$
- $2\times3 = 6$
- $2\times4 =8$
- $2\times5 =10$
- $2\times6 =12$
- $2\times7 = 14$
- $2\times8 = 16$
- $2\times9 = 18$
- $2\times10= 20$
So if Alex knows the table of two, he can skip the tedious calculations. A single pair of shoes consists of two shoes, so we can calculate the total number of shoes in $10$ pairs as $2\times10 =20.$ So instead of counting them one by one, Alex can easily calculate the total number of shoes by using the table of $2$.
Different Tips for Learning the $2$ Times Table
$2$ times table is the simplest of all the tables, and it is easy to learn and memorize. Let us look at some simple tips which can help you memorize the 2 times table.
- Recitation: Students who are having difficulty in addition or multiplication can recite the two times table loudly and repeatedly. Recitation can be done like this:
1 times 2 is 2
2 times 2 is 4
3 times 2 is 6
4 times 2 is 8
5 times 2 is 10
6 times 2 is 12
7 times 2 is 14
8 times 2 is 16
9 times 2 is 18
10 times 2 is 20
- Addition: One of the easiest ways of memorizing the 2 times table for elementary students is using the addition method. Once they have memorized the table, they would not need the addition technique for more involved problems. In the addition method, the first step is adding $2$ and $0$, i.e., $0+2 =2$. Then, in each next step, we add a $2$ in the result of the previous step. The result of the first step is $2$, so the result of the second step will be $2 + 2 = 4$. Similarly, the result of the third step will be $4+2=6$, and so on.

- Multiple of 2: The second method is using multiples of two or just following the patterns of even numbers. The first five multiples of 2 can be written as:
First multiple of $2 = 2$
Second multiple of $2 = 4$
Third multiple of $2 = 6$
Fourth multiple of $2 = 8$
Fifth multiple of $2 = 10$
- Even number sequence: All the multiples of 2 are divisible by 2 and are even numbers. If the sequence of even numbers is followed, we will get all the multiples of 2 (as already described in the previous method).
- 1 times table: 1 times table can also be used to understand and memorize $2$ times table. This method is good for those students who are having a hard time cramming the $2$ times table and prefer to memorize the table through basic written form. All we have to do is write the 1 times table and add natural numbers in sequence / or each answer to itself. Natural numbers can be represented as:
$N = {1, 2, 3, 4, 5, 6……}$
$(1\times1) = 1$ so if we add the answer to itself we get $1+1 = 2$ or by adding first natural number to $(1×1)+1 =1+1=2$.
$(1\times2)+2 = 2+2 = 4$
$(1\times3)+3 = 6$
$(1\times4)+4 = 8$
$(1\times5)+5 = 10$
$(1\times6)+6 = 12$
$(1\times7)+7 = 14$
$(1\times8)+8 = 16$
$(1\times9)+9 = 18$
$(1\times10)+10 = 20$
Note that all the answers are even numbers and are sequential multiples of $2$, so arranging them in sequence will give us the $2$ times table.
Table of 2 From 1 to 15:
A complete table of $2$ from $1$ to $15$ can be written as:
Numerical Representation | Descriptive Representation | Product (Answer) |
| $1\times2$ | One times two | $2$ |
| $2\times2$ | Two times two | $4$ |
| $3\times2$ | Three times two | $6$ |
| $4\times2$ | Four times two | $8$ |
| $5\times2$ | Five times two | $10$ |
| $6\times2$ | Six times two | $12$ |
| $7\times2$ | Seven times two | $14$ |
| $8\times2$ | Eight times two | $16$ |
| $9\times2$ | Nine times two | $18$ |
| $10\times2$ | Ten times two | $20$ |
| $11\times2$ | Eleven times two | $22$ |
| $12\times2$ | Twelve times two | $24$ |
| $13\times2$ | Thirteen times two | $26$ |
| $14\times2$ | Fourteen times two | $28$ |
| $15\times2$ | Fifteen times two | $30$ |
Example 1: Using the $2$ times table, find the 8th multiple of $2$.
Solution:
The 8th multiple of 2 can be calculated simply as $2×8 =16$.
Example 2: From number $1$ to 50, highlight the numbers which are multiples of $2$
Solution:
All even numbers are multiples of $2$, and these numbers are also the outcomes of the 2 times table.
| 1 | 2 | 3 | 4 | 5 |
| 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 |
| 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 |
| 46 | 47 | 48 | 49 | 50 |
Example 3: Simon loves to make drawings. He takes two days to make a drawing. How many days will he take to make four drawings?
Solution:
Let’s first use simple addition to find the answer. Simon will take $2$ days to make the first drawing. Then, he will take $2+2=4$ days to make two drawings. Then, $4+2=6$ days for three drawings and finally $6+2 =8$ days to make four drawings. So the answer is $8$.
Now let’s solve it using the two times table. It takes $2$ days to make one drawing, so it will take $2 \times 4$ days to make $4$ drawings. From the two times table, we see that $2 \times 4 = 8$, so the answer is $8$.
Example 4: Anny gets pocket money of $2$ dollars every day. What will be the total amount of pocket money at the end of the week?
Solution:
We know that a week has $7$ days in it. So by using the $2$ times table, we can calculate the total amount of pocket money $2×7 = 14$.
Practice Questions:
- Alex wants to purchase five chocolates, and the price of one chocolate is $2. Calculate the total cost of five chocolates using the 2 times table?
- Steve collects stamps as a hobby. If Steve collects 2 stamps a day, how many stamps will he have at the end of 10 days?
- What is the product/answer of 2 times 2 times 2?
- From the given table, select the numbers which are multiples of 2.
| 17 | 15 | 35 | 4 | 5 |
| 25 | 19 | 20 | 22 | 10 |
| 0 | 1 | 3 | 11 | 15 |
| 16 | 18 | 24 | 8 | 20 |
| 21 | 2 | 6 | 9 | 25 |
| 44 | 14 | 15 | 29 | 30 |
| 33 | 32 | 31 | 34 | 35 |
| 39 | 37 | 26 | 39 | 40 |
| 41 | 42 | 43 | 50 | 45 |
| 44 | 57 | 59 | 49 | 60 |
Answer Key:
- The total cost of $5$ chocolates will be $ 2\times5 = 10 $ dollars
- The total amount of stamps collected by Steve will be $2\times10 = 20$ stamps
- This question can be solved in two ways. We are given three 2s, and we have to find their product
- If we use the multiples of 2 method: $ 2\times2\times2 = 8 $
- By using 2 times table, we know we are given three 2s so, $ 2\times3 = 8 $
4)
| 17 | 15 | 35 | 4 | 5 |
| 25 | 19 | 20 | 22 | 10 |
| 0 | 1 | 3 | 11 | 15 |
| 16 | 18 | 24 | 8 | 20 |
| 21 | 2 | 6 | 9 | 25 |
| 44 | 14 | 15 | 29 | 30 |
| 33 | 32 | 31 | 34 | 35 |
| 39 | 37 | 26 | 39 | 40 |
| 41 | 42 | 43 | 50 | 45 |
| 44 | 57 | 59 | 49 | 60 |
